


苏教版 (2019)必修 第二册14.3 统计图表精品课后复习题
展开知识点01 扇形统计图、折线统计图、频数直方图
【即学即练1】(多选题)(2024·高三·全国·专题练习)[多选]工业生产者出厂价格指数(PPI)是反映工业企业产品第一次出售时的出厂价格的变化趋势和变动幅度,是反映某一时期生产领域价格变动情况的重要经济指标,也是制定有关经济政策和国民经济核算的重要依据.根据下面提供的我国2020年1月—2021年11月的工业生产者出厂价格指数的月度同比(将上一年同月作为基期进行对比的价格指数)和月度环比(将上月作为基期进行对比的价格指数)涨跌情况的折线图判断,以下结论不正确的是( )
A.2020年各月的PPI在逐月增大
B.2020年各月的PPI均高于2019年同期水平
C.2021年1月—2021年11月各月的PPI在逐月减小
D.2021年1月—2021年11月各月的PPI均高于2020年同期水平
【答案】ABC
【解析】对于A,2020年前5个月的PPI月度环比增长均为负值,即在逐月减小,故A错误;
对于B,2020年2月之后各月的PPI月度同比增长均为负值,即低于2019年同期水平,故B错误;
对于C,2021年1月—2021年11月各月的PPI月度环比增长均不为负,即逐月增大,故C错误;
对于D,2021年1月—2021年11月各月的PPI月度同比增长均为正值,即高于2020年同期水平,故D正确.
故选:ABC.
知识点02 频率分布表
频率分布直方图绘制步骤
①求极差,即一组数据中的最大值与最小值的差.
②决定组距与组数.组距与组数的确定没有固定的标准,一般数据的个数越多,所分组数越多.当样本容量不超过100时,常分成5~12组.为方便起见,一般取等长组距,并且组距应力求“取整”.
③将数据分组.
④列频率分布表.计算各小组的频率,第i组的频率是.
⑤画频率分布直方图.其中横轴表示分组,纵轴表示,实际上就是频率分布直方图中各小长方形的高度,它反映了各组样本观测数据的疏密程度.
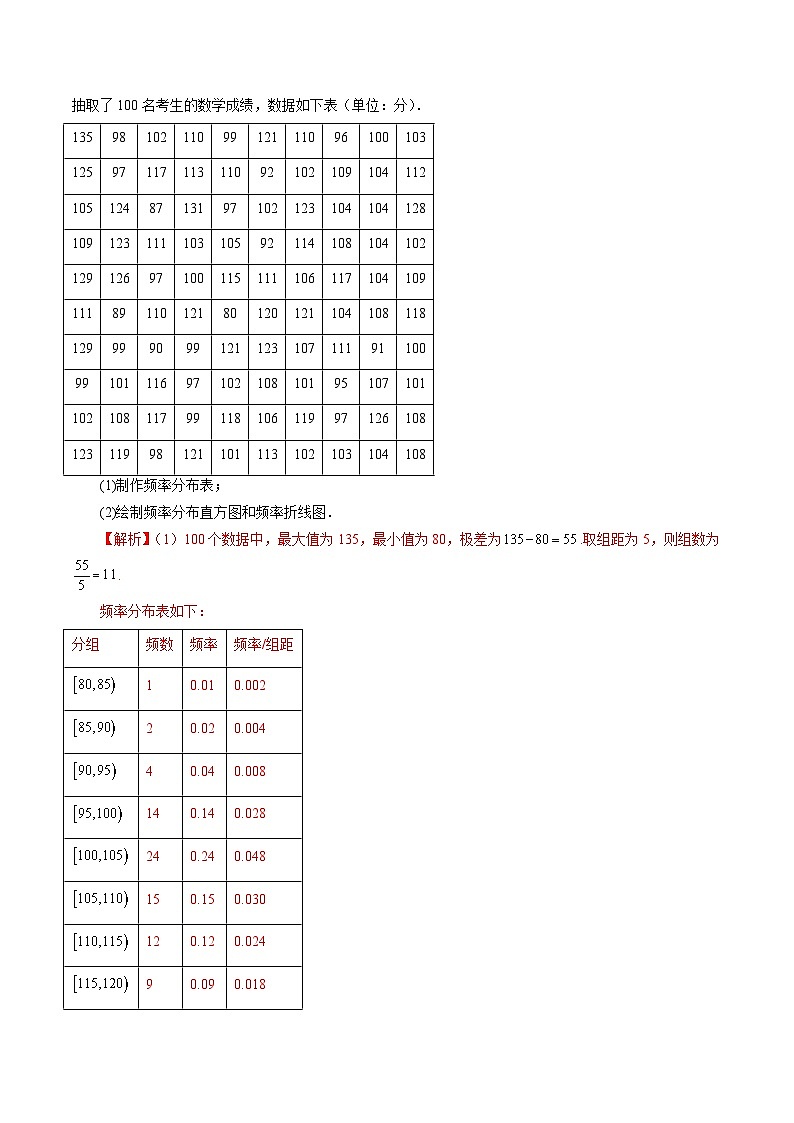
【即学即练2】(2024·高二·全国·课时练习)某省为了了解和掌握今年高考考生的实际答题情况,随机抽取了100名考生的数学成绩,数据如下表(单位:分).
(1)制作频率分布表;
(2)绘制频率分布直方图和频率折线图.
【解析】(1)100个数据中,最大值为135,最小值为80,极差为.取组距为5,则组数为.
频率分布表如下:
注:表中加上“频率/组距”一列,这是为画频率分布直方图准备的,因为它是频率分布直方图的纵坐标.
(2)根据频率分布表中的有关信息画出频率分布直方图及折线图,如图所示.
知识点03 频率直方图与折线图
1、频率分布直方图意义:各个小长方形的面积表示相应各组的频率,频率分布直方图以面积的形式反映数据落在各个小组的频率的大小,各小长方形的面积的总和等于1.
2、总体取值规律的估计:我们可以用样本观测数据的频率分布估计总体的取值规律.
3、频率分布直方图的特征:当频率分布直方图的组数少、组距大时,容易从中看出数据整体的分布特点,但由于无法看出每组内的数据分布情况,损失了较多的原式数据信息;当频率分布直方图的组数多、组距小时,保留了较多的原始数据信息,但由于小长方形较多,有时图形会变得非常不规则,不容易从中看出总体数据的分布特点.
4、常见的其他统计图:条形图、扇形图、折线图.
扇形图主要用于直观描述各类数据占总数的比例;
条形图和直方图主要用于直观描述不同类别或分组数据的频数和频率;
折线图主要用于描述数据随时间的变化趋势.
5、各个统计图特点
(1)不同的统计图在表示数据上有不同的特点.如扇形图主要用于直观描述各类数据占总数的比例,条形图和直方图主要用于直观描述不同类别或分组数据的频数和频率,折线图主要用于描述数据随时间的变化趋势.
(2)不同的统计图适用的数据类型也不同.如条形图适用于描述离散型的数据,直方图适用于描述连续性数据.
【即学即练3】(2024·高一·江苏·专题练习)某校公布了该校反映各年级学生体育达标情况的两张统计图(如图),该校七、八、九三个年级共有学生800人,甲、乙、丙三个同学看了这两张统计图后,甲说:“七年级的体育达标率最高”.乙说:“八年级共有学生264人.”丙说:“九年级的体育达标率最高.”甲、乙、丙三个同学中,说法正确的是( )
A.甲和乙B.乙和丙
C.甲和丙D.甲、乙和丙
【答案】B
【解析】由扇形统计图可得八年级共有学生(人),
七年级共有学生(人),
九年级共有学生(人),
所以七年级的达标率为;
九年级的达标率为;
八年级的达标率为.
则九年级的达标率最高,则乙、丙的说法是正确的.
故选:B.
题型一:频率分布直方图的绘制与应用
【典例1-1】(2024·高一·全国·随堂练习)一种袋装食品用生产线自动装填,每袋质量大约为50g,但由于某些原因,每袋食品不会恰好是50g.现随机抽取100袋食品,测得的质量数据如下:
单位:g
(1)为了获得样本数据的分布情况,试制作频率分布表;
(2)绘制频率分布直方图及频率分布折线图.
【解析】(1)1.计算极差,这组数据中,最大值为61,最小值为40,故极差为,
【典例1-2】确定组数和组距,样本量在100左右,可取个组,由于,故不妨取11个组,组距定为,
【变式1-1】频率分布表如下:
(2)频率分布直方图如下:
频率分布折线图如下:
【变式1-2】(2024·高一·全国·课堂例题)某校高一年级共有450名男生,为了解他们的身高情况,从中随机抽查了50名学生,测得他们的身高数据(单位:cm)如下:
151 153 157 159 160 161 162 163 163 164
164 164 165 165 166 166 167 167 168 168
169 169 169 170 170 170 171 171 172 172
172 173 173 173 173 173 174 175 175 176
176 177 177 178 178 179 180 181 181 183
(1)列出频率分布表并画出频率分布直方图;
(2)估算该年级身高在内的男生人数;
(3)估算该年级身高在170cm以下的男生人数.
【解析】(1)这组数据的最大值为183,最小值为151,极差为32.
为分组的方便,取略大的身高范围,同时取组距为5,分为7组.
计算相应的分组频率,就得到下面的频率分布表.
绘制频率分布直方图,如图.
(2)由频率分布表和频率分布直方图可以估计,总体中约有的男生身高在内.
由于全年级共有450名男生,所以该年级身高在内的男生大约有(人).
(3)样本中身高在170cm以下的男生所占比例约为,
所以该年级身高在170cm以下的男生大约有(人).
【变式1-3】(2024·高一·辽宁阜新·阶段练习)有一个容量为60的样本(60名学生的数学考试成绩),分组情况如下表:
(1)补全表中所剩的空格;
(2)画出频率分布直方图和频率分布折线图.
【解析】(1)根据题意,的频率为;的频率为;
的频率为;的频率为,
频数为;的频数为.
填表如下.
(2)计算的,的,
的,的,
的.
画出的频率分布直方图和频率分布折线图如图所示.
【变式1-4】(2024·高一·全国·单元测试)下面是一次考试几个班同学的数学成绩(单位:分,满分为150分):
121,111,128,98,118,124,137,125,121,140,
129,122,101,103,134,126,129,132,99,132,
141,125,122,120,139,106,142,119,134,119,
122,126,114,141,132,125,111,145,110,123,
118,127,129,141,103,117,116,131,134,143,
113,142,125,136,119,110,107,124,137,100,
115,144,96,138,120,121,140,115,123,142,
119,133,120,146,119,144,119,122,119,136,
137,132,112,133,134,117,127,133,126,127,
141,119,131,131,123,128,133,126,129,134,
127,133,121,135,107,132,121,137,118,117,
107,133,131,131,125,126,140,127,114,136,
118,138,127,143,81,140,135,137,142,136,
139,124,138,119,122,136,141,119,118,114.
(1)你觉得怎样直观地表示出上述数据的大致分布情况(比如哪个分数段的人数比较多,哪个分数段的人数比较少)?
(2)画出频率分布直方图,看这次考试的整体分布,能说明哪些问题?
【解析】(1)数据比较多的时候,要想获得数据的大致分布情况,
最好借助我们学过的图表,比如频率分布表、频率分布直方图.
(2)列频率分布表如下:
画频率分布直方图,如图所示:
通过频率分布直方图我们可以看到,
大部分同学的成绩集中在分数段内,
说明本次考试成绩难度不大,而个别同学成绩较低,
可能学习上遇到了困难,应该引起关注.
【变式1-5】(2024·高一·全国·课后作业)考查某校高三年级男同学的身高,随机地抽取50名男同学,测得他们的身高(单位:cm)如下表所示:
(1)这组数据的极差为______,数据160的频数为______,数据171的频率为______;
(2)填写下面的频率分布表:
(3)画出该校高三年级男同学身高的频率分布直方图.
【解析】(1)因为最高身高为180,最低身高为151,所以极差为:180-151=29;
因为身高为160的人数为4,所以频数为4;
因为身高为171的人数为3,所以频率为;
(2)填表如下:
(3)由频率分布表,可得频率分布直方图,如下:
【方法技巧与总结】(绘制频率分布直方图的注意事项)
1、在列频率分布表时,极差、组距、组数有如下关系:
(1)若eq \f(极差,组距)为整数,则eq \f(极差,组距)=组数;
(2)若eq \f(极差,组距)不为整数,则eq \f(极差,组距)的整数部分+1=组数.
2、组距和组数的确定没有固定的标准,将数据分组时,组数力求合适,纵使数据的分布规律能较清楚地呈现出来,组数太多或太少,都会影响我们了解数据的分布情况,若样本容量不超过100,按照数据的多少常分为5~12组,一般样本容量越大,所分组数越多.
题型二:频率分布直方图中的相关计算问题
【典例2-1】(2024·高一·全国·课时练习)2019年1月1日,“学习强国”学习平台在全国上线,某单位组织全体党员登录学习统计学习积分得到的频率分布直方图如图所示.若学习积分在(单位:万分)的人数是32人,则该单位共有 名党员,若学习积分超过2万分的党员可获得“学习达人”称号,则该单位有 名党员能获得该称号.
【答案】 80 8
【解析】由频率分布直方图得:学习积分在(单位:万分)的频率为,
因为学习积分在(单位:万分)的人数是32人,所以该单位有(人);
因为学习积分超过2万分的党员可获得“学习达人”称号,且学习积分超过2万分的频率为,
所以该单位有名党员能获得该称号.
故答案为:80;8.
【典例2-2】(2024·高一·全国·专题练习)一个社区调查机构就某地居民的月收入(百元)调查了10000人,将所得数据分成如下六组:,,,,,,然后得到如图所示的频率分布直方图.若将这10000人按其月收入也分成相应六组,并进行分层抽样抽出200人作进一步调查,则在这一组中应抽出 人.
【答案】50
【解析】由频率分布直方图可知这一组所对应频率为,
又分层抽样人数为200人,则应抽取(人).
故答案为:.
【变式2-1】(2024·高一·天津·期末)从某校高一年级学生中随机抽取了20名学生,将他们的数学检测成绩分成六段(满分100分,成绩均为不低于40分的整数):,得到如图所示的频率分布直方图,则得分在内的人数为 .
【答案】
【解析】因为频率分布直方图中所有小矩形面积和为1,
所以,解得,
所以分数在内的人数为.
故答案为:6.
【变式2-2】(2024·高一·全国·课时练习)为了解某校高三学生联考的数学成绩情况,从该校参加联考学生的数学成绩中抽取一个样本,并分成五组,绘成如图所示的频率分布直方图.已知第一组至第五组的频率之比为,第五组的频数为6,则样本容量为 .
【答案】40
【解析】因为第一组至第五组的频率之比为,
可设第一组至第五组的频率分别为,,,,,又频率之和为1,
所以,解得,
第五组的频率为,又第五组的频数为6,
所以样本容量为.
故答案为:40.
【变式2-3】(2024·高一·江苏苏州·期末)为抗击新型冠状病毒,普及防护知识,某校开展了“疫情防护”网络知识竞赛活动,现从参加该活动的学生中随机抽取了100名学生,将他们的比赛成绩(满分为100分)分为5组:,,,,,得到如图所示的频率分布直方图,则该100名学生中成绩在80分(含80分)以上的人数为 .
【答案】40
【解析】由题可得,解得:;
该100名学生中成绩在80分(含80分)以上的人数为人,
故答案为:40.
【变式2-4】(2024·高三·湖南长沙·阶段练习)为了解某市居民用水情况,通过抽样,获得了100位居民某年的月均用水量(单位:吨),将该数据按照[0,0.5),[0.5,1),…[4.4.5]分成9组,绘制了如图所示的频率分布直方图,政府要试行居民用水定额管理,制定了一个用水量标准,使85%的居民用水量不超过(假设为整数),按平价收水费,超出的部分按议价收费,则的最小值为 .
【答案】3吨
【解析】求出,的频数为4,,的频数为8,,的频数为22,,的频数为25,,的频数为4,,的频数为4,,的频数为2,,由此能求出的最小值.,的频数为,
,的频数为,
,的频数为,
,的频数为,
,的频数为.
,的频数为,
,的频数为,
,
前6组占,为3吨.
故答案为:3吨.
【变式2-5】(2024·高一·全国·课时练习)某商场为了了解某日旅游鞋的销售情况,抽取了部分顾客所购鞋的尺寸,将所得数据整理后,画出频率分布直方图如图所示.已知从左到右前3个小组的频率之比为1∶2∶3,第4小组与第5小组的频率分布如图所示,第2小组的频数为10,则第4小组顾客的人数是 .
【答案】15
【解析】先求得第4小组与第5小组的频率,结合前3个小组的频率之比为1∶2∶3,即可求得各组的频率.结合第2小组的频数为10,可求得抽取的总人数,即可由第4组的频率求得第4组的人数.由题意得第4小组与第5小组的频率分别为和,
所以前3组的频率之和为0.6.又因为从左到右前3个小组的频率之比为1∶2∶3,
所以从左到右第2小组的频率为0.2.因为第2小组的频数为10,
所以抽取的顾客人数是.
故第4小组顾客的人数是.
故答案为:15
【变式2-6】(2024·高一·全国·课时练习)对某活动中800名志愿者的年龄抽样调查,统计后得到频率分布直方图(如图),但是年龄组的数据不慎丢失,依据此图回答以下问题.
(1)年龄组对应小矩形的高度为 ;
(2)据此估计本次活动中志愿者年龄在内的人数为 .
【答案】 0.04. 440.
【解析】(1)通过频率分布直方图中各小长方形面积之和为1,列方程计算即可;
(2)先计算出志愿者年龄在内的频率,再计算人数即可.(1)设年龄组对应小矩形的高度为,则,解得;
(2)由(l)得志愿者年龄在内的频率为,故志愿者年龄在内的人数约为.
故答案为:(l)0.04;(2)440
【方法技巧与总结】(计算规律)
1、因为小长方形的面积=组距×频率组距=频率,所以各小长方形的面积表示相应各组的频率.这样,频率分布直方图就以面积的形式反映了数据落在各个小组内的频率大小.
2、在频率分布直方图中,各小长方形的面积之和等于1.
3、频数相应的频率=样本量.
4、在频率分布直方图中,各长方形的面积之比等于频率之比,各长方形的高度之比也等于频率之比.
题型三:对折线图、扇形图、条形图的识读
【典例3-1】(2024·江西鹰潭·一模)南丁格尔玫瑰图是由近代护理学和护士教育创始人南丁格尔(Flrence Nightingale)设计的,图中每个扇形圆心角都是相等的,半径长短表示数量大小.某机构统计了近几年中国知识付费用户数量(单位:亿人次),并绘制成南丁格尔玫瑰图(如图所示),根据此图,以下说法正确的是( )
A.2015年至2022年,知识付费用户数量先增加后减少
B.2015年至2022年,知识付费用户数量逐年增加量2022年最多
C.2015年至2022年,知识付费用户数量的逐年增加量逐年递增
D.2022年知识付费用户数量超过2015年知识付费用户数量的10倍
【答案】D
【解析】对于A,由图可知,2015年至2022年,知识付费用户数量逐年增加,故A错误;
对于BC,知识付费用户数量的逐年增加量分别为:
2016年,;2017年,;
2018年,;2019年,;
2020年,;2021年,;
2022年,;
则知识付费用户数量逐年增加量2018年最多,
知识付费用户数量的逐年增加量不是逐年递增,故BC错误;
对于D,由,
则2022年知识付费用户数量超过2015年知识付费用户数量的10倍,故D正确.
故选:D.
【典例3-2】(2024·高一·全国·专题练习)王老师对本班名学生报名参与课外兴趣小组(每位学生限报一个项目)的情况进行了统计,列出如下的统计表,则本班报名参加科技小组的人数是( )
A.人B.人C.人D.人
【答案】A
【解析】参加科技小组的频率为,则本班报名参加科技小组的人数是人.
故选:A.
【变式3-1】(2024·甘肃·一模)小李一周的总开支分布如图(1)所示,其中一周的食品开支如图(2)所示,则以下判断错误的是( )
A.小李这一周用于肉蛋奶的支出高于用于娱乐的支出
B.小李这一周用于食品中其他类的支出在总支出中是最少的
C.小李这一周用于主食的支出比用于通信的支出高
D.小李这一周用于主食和蔬菜的总支出比日常支出高
【答案】D
【解析】对于A,肉蛋奶的支出占食品开支的,
从而小李这一周用于肉蛋奶的支出占比(总开支是单位1)与用于娱乐的支出占比(总开支是单位1)大小关系为,故A描述正确,不符合题意;
对于B,小李这一周用于食品中其他类的支出在总支出中占比为,
对比其他类型的支出占比可知,B描述正确,不符合题意;
对于C,小李这一周用于主食的支出占比(总开支是单位1)与通信的支出占比(总开支是单位1)的大小关系为,
,故C描述正确,不符合题意;
对于D,小李这一周用于主食和蔬菜的总支出占比(总开支是单位1)与日常支出占比(总开支是单位1)的大小关系为,
,故D描述错误,符合题意.
故选:D.
【变式3-2】(2024·高一·全国·期末)为迎接党的二十大胜利召开,某校开展了“学党史,悟初心”系列活动.学校对学生参加各项活动的人数进行了调查,并将数据绘制成如下统计图.若参加“书法”的人数为80人,则参加“大合唱”的人数为( )
A.60人B.100人C.160人D.400人
【答案】C
【解析】由题意大合唱的所占比例为,
因为参加“书法”的比例为,人数为80人,所以参加“大合唱”的人数为160人.
故选:C
【变式3-3】(多选题)(2024·高二·湖南·阶段练习)为了解各种APP的使用情况,将使用人数排名前5的数据整理得到如下的柱状图,则( )
A.APP使用人数最多的是微信
B.微信APP的使用人数超过今日头条APP的使用人数的2倍
C.微信APP的使用人数超过今日头条APP与快手APP的使用人数之和
D.抖音APP的使用人数大于快手APP的使用人数的125%
【答案】AD
【解析】对于A中,根据数据的柱状图,可得APP使用人数最多的是微信,所以A正确;
对于B中,微信APP的使用人数占7格,今日头条APP的使用人数占近4格,
所以微信APP的使用人数小于今日头条APP的使用人数的2倍,所以B错误;
对于C中,微信APP的使用人数占7格,今日头条APP的使用人数占近4格,快手APP的使用人数占4格,
所以微信APP的使用人数小于今日头条APP与快手APP的使用人数之和,所以C错误;
对于D中,抖音APP的使用人数占5格多,快手APP的使用人数占4格,
则快手APP的使用人数的等于5格,
所以抖音APP的使用人数大于快手APP的使用人数的,所以D正确.
故选:AD.
【变式3-4】(多选题)(2024·高二·福建泉州·期末)2020年1月17日,国家统计局发布了2019年全国居民人均消费支出及其构成的情况,并绘制了如图的饼图.根据饼图判断,下列说法不正确的是( )
A.2019年居民在“生活用品及服务”上人均消费支出的占比为6%
B.2019年居民人均消费支出为23350元
C.2019年居民在“教育文化娱乐”上人均消费支出小于这8项人均消费支出的平均数
D.2019年居民在“教育文化娱乐”、“生活用品及服务”、“衣着”上的人均消费支出之和大于在“食品烟酒”上的人均消费支出
【答案】BD
【解析】选项A,,故A正确;
选项B,由题意,在“生活用品及服务”上人均消费支出的占比为6%,且支出为1281元,
则2019年居民人均消费支出为元,故B错误;
选项C,2019年居民在“教育文化娱乐”上人均消费支出占比,故C正确:
选项D,2019年居民在“教育文化娱乐”、“生活用品及服务”、“衣着”上的人均消费支出占比之和为,故D错误.
故选:BD.
【方法技巧与总结】(各类统计图的特点)
条形统计图反映各组数据的频数或频率;
扇形统计图反映各组数据占总数的比例;
折线统计图反映数据随时间的变化趋势.
一、单选题
1.(2024·海南·模拟预测)某机构统计了1000名演员的学历情况,制作出如图所示的饼状图,其中本科学历的人数为630.现按比例用分层随机抽样的方法从中抽取200人,则抽取的硕士学历的人数为( )
A.11B.13C.22D.26
【答案】D
【解析】由题意硕士学历的人数与总人数1000之比为,
现按比例用分层随机抽样的方法从中抽取200人,则抽取的硕士学历的人数为.
故选:D.
2.(2024·贵州贵阳·一模)为了树立和践行绿水青山就是金山银山的理念,市某高中全体教师于2023年3月12日开展植树活动,购买柳树、银杏、梧桐、樟树四种树苗共计1200棵,比例如图所示.青年教师、中年教师、老年教师报名参加植树活动的人数之比为,若每种树苗均按各年龄段报名人数的比例进行分配,则中年教师应分得梧桐的数量为( )
A.60棵B.100棵C.144棵D.160棵
【答案】C
【解析】由题意,中年教师应分得树苗的数量为棵,
所以中年教师应分得梧桐的数量为棵,
故选:C
3.(2024·高三·全国·专题练习)在样本频率分布直方图中共有9个小矩形,若其中1个小矩形的面积等于其他8个小矩形面积和的,且样本容量为210,则该组的频数为( ).
A.28B.40C.56D.60
【答案】D
【解析】设该小矩形的面积为x,9个小矩形的总面积为1,
则其他8个小矩形的面积和为,所以,
所以,所以该组的频数为.
故选:D.
4.(2024·高三·四川成都·期末)下图是2023年1~12月份品种能源生产当月同比增长率情况变化图.下列说法错误的是( )
A.4~7月,原煤及天然气当月同比增长率呈下降趋势
B.9~12月,原煤及天然气当月同比增长率总体呈上升趋势
C.7月份品种能源生产当月同比增长率最高的是原油加工量同比增长率
D.2023年品种能源生产当月同比增长率波动最小的是发电量同比增长率
【答案】D
【解析】观察题中所给的折线图,可知:
4~7月,原煤及天然气当月同比增长率是下降的,呈下降趋势,所以A项正确;
9~12月,虽然天然气11月比10月偏低,但总体趋势仍为上升的,
所以原煤及天然气当月同比增长率总体呈上升趋势,所以B正确;
图中7月份,只有原煤加工上升,其他品种能源均比6月份低,所以C项正确;
由图易知,相比发电量,原油的曲线波动幅度更小,所以D项错误;
故选:D.
5.(2024·高三·全国·专题练习)为了解某小区户主对楼层的满意程度,用分层随机抽样的方法抽取40%的户主进行调查,已知该居民小区户主人数和户主对楼层的满意率分别如图1和图2所示,则样本容量和抽取的低层户主中满意的人数分别为( ).
A.240,32B.320,32C.240,80D.320,80
【答案】B
【解析】由图1所示,可得小区共有(人),
则样本容量为(人).
低层户主共有400人,满意率为20%,
故抽取的低层户主中满意的人数为(人).
故选:B.
6.(2024·全国·模拟预测)某校高三年级有(1),(2),(3)三个班,一次期末考试后,统计得到每班学生的数学成绩的优秀率(数学成绩在120分以上的学生人数与该班学生总人数之比)如表所示:
则下列说法错误的是( )
A.(2)班学生的数学成绩的优秀率最高
B.(3)班学生的数学成绩优秀人数不一定最少
C.该年级全体学生数学成绩的优秀率为
D.若把(1)班和(2)班的数学成绩放在一起统计,得到优秀率为,则(1)班人数少于(2)班人数
【答案】C
【解析】选项A:显然(2)班学生的数学成绩的优秀率最高,故A正确;
选项B:只根据优秀率的大小,无法比较每班学生的数学成绩优秀人数多少,故B正确;
对于C:全体学生数学成绩的优秀率为全年级数学成绩优秀的学生人数与全年级学生总人数之比,
由于各班的学生人数不知道,所以不能计算该年级全体学生数学成绩的优秀率,故C不正确;
对于D:设(1)班、(2)班数学成绩优秀的人数分别为,,(1)班、(2)班人数分别为,
则,得,
又(1)班和(2)班放在一起统计的优秀率为,
所以,即,可得,则,故D正确.
故选:C.
7.(2024·高一·河南开封·期中)汽车的“燃油效率”是指汽车每消耗1升汽油行驶的里程,如图描述了甲、乙、丙三辆汽车在不同速度下的燃油效率情况.下列叙述中正确的是( )
①某城市机动车最高限速80千米/小时,相同条件下,在该市用丙车比用乙车更省油.
②消耗1升汽油,乙车最多可行驶5千米;
③以相同速度行驶相同路程,三辆车中,甲车消耗汽油最少;
④甲车以80千米/小时的速度行驶1小时,消耗10升汽油
A.②④B.①③C.①②D.③④
【答案】B
【解析】对于①,速度在80千米小时以下时,相同条件下每消耗1升汽油,
丙车行驶路程比乙车多,所以该市用丙车比用乙车更省油,所以①正确;
对于②,从图中可以看出乙车的最高燃油效率大于5(乙车图象的最高点的纵坐标大于,所以②错误;
对于③,同样速度甲车消耗1升汽油行驶的路程比乙车、丙车的多,
所以行驶相同路程,甲车油耗最少,所以③正确;
对于④,甲车以80千米小时的速度行驶,1升汽油行驶10千米,
所以行驶1小时,即行驶80千米,消耗8升汽油,所以④错误.
故选:B.
8.(2024·高二·四川眉山·期末)对某种灯泡随机地抽取200个样品进行使用寿命调查,结果如下:
规定:使用寿命大于或等于500天的灯泡是优等品,小于300天是次品,其余的是正品.现从灯泡样品中随机地抽取个,若这n个灯泡的等级分布情况恰好与从这200个样品中按三个等级分层抽样所得的结果相同,则n的最小值为( )
A.2B.3C.4D.5
【答案】C
【解析】由频率分布表,得,
故灯泡样品中优等品有50个,正品有100个,次品有50个,
优等品、正品、次品的比为.
按分层抽样方法,抽取灯泡的个数,故的最小值为4,
故选:C.
二、多选题
9.(2024·高一·江苏·专题练习)为比较甲、乙两名学生的数学学科素养的各项能力指标值(满分为5分,分值高者为优),绘制了如图所示的六维能力雷达图,例如图中甲的数学抽象指标值为4,乙的数学抽象指标值为5,则下面叙述正确的是( )
A.甲的逻辑推理能力指标值优于乙的逻辑推理能力指标值
B.甲的数学建模能力指标值优于乙的直观想象能力指标值
C.乙的六维能力指标值整体水平优于甲的六维能力指标值整体水平
D.甲的数学运算能力指标值优于甲的直观想象能力指标值
【答案】AC
【解析】对于A,甲的逻辑推理能力指标值为4,优于乙的逻辑推理能力指标值为3,故A正确.
对于B,甲的数学建模能力指标值为3,乙的直观想象能力指标值为5,
所以乙的直观想象能力指标值优于甲的数学建模能力指标值,故B错误.
对于C,甲的六维能力指标值的平均值为,
乙的六维能力指标值的平均值为,因为,故C正确.
对于D,甲的数学运算能力指标值为4,甲的直观想象能力指标值为5,
所以甲的数学运算能力指标值不优于甲的直观想象能力指标值,故D错误.
故选:AC.
10.(2024·高一·江苏·专题练习)(多选)某报告显示:我国农民工收入持续快速增长.某地区农民工人均月收入增长率如图①,并将人均月收入绘制成如图②的不完整的条形统计图.
根据以上统计图,以下说法正确的是( )
A.2020年农民工人均月收入的增长率是10%
B.2018年农民工人均月收入是2 205元
C.小明认为“农民工2019年的人均月收入比2018年的少了”
D.2016年到2020年这五年中,2020年农民工人均月收入最高
【答案】ABD
【解析】A选项,由折线统计图,知2020年农民工人均月收入的增长率是10%,则A正确;
B选项,由条形统计图,知2018年农民工人均月收入是2205元,则B正确;
C选项,由题图,知2019年农民工人均月收入为,故C说法错误.
D选项,由条形统计图,知2016年到2020年这五年中,2020年农民工人均月收入最高,则D说法正确.
故选:ABD.
11.(2024·高一·辽宁·期末)为了了解某社区用水量情况,对该社区居民去年的月均用水量进行抽样调查,整理该社区居民去年的月均用水量的数据,得到如下频率分布直方图.根据此频率分布直方图,下列结论正确的是( )
A.该社区居民去年的月均用水量高于9吨的用户比率估计为
B.估计该社区去年有一半的居民月均用水量在5吨到9吨之间
C.若该社区有1000户居民,估计该社区去年月均用水量不足3吨的用户有100户
D.估计该社区居民去年的月均用水量的平均值大于7吨(同一组中的数据用该组区间的中点值代替)
【答案】BCD
【解析】对A:该社区居民去年的月均用水量高于吨的比率估计为,故A错误.
对B:该社区去年有一半的居民月均用水量在吨到吨之间为,故B正确.
对C:估计该社区去年月均用水量不足吨的户数为,故C正确.
对D:月均用水量的平均值为,故D正确.
故选:BCD.
12.(2024·高三·广东深圳·期末)为丰富优质旅游资源,释放旅游消费潜力,推动旅游业高质量发展,某地政府从2023年国庆期间到该地旅游的游客中,随机抽取部分游客进行调查,得到各年龄段游客的人数和对景区服务是否满意的数据,并绘制统计图如图所示,利用数据统计图估计,得到的结论正确的是( )
A.游客中,青年人是老年人的2倍多
B.老年人的满意人数是青年人的2倍
C.到该地旅游的游客中满意的中年人占总游客人数的24.5%
D.到该地旅游的游客满意人数超过一半
【答案】ACD
【解析】由扇形统计图可知青年人占比是老年人占比的2倍多,故A正确;
其中满意的青年人占总人数的,
满意的中年人占总人数的,
满意的老年人占总人数的,故B错误,C正确;
总满意率为,故D正确.
故选:.
三、填空题
13.(2024·高三·北京·期中)下表是某生活超市2021年第四季度各区域营业收入占比和净利润占比统计表:
该生活超市本季度的总营业利润率为(营业利润率是净利润占营业收入的百分比),给出下列四个结论:
①本季度此生活超市营业收入最低的是熟食区:
②本季度此生活超市的营业净利润超过一半来自生鲜区;
③本季度此生活超市营业利润率最高的是日用品区;
④本季度此生活超市生鲜区的营业利润率超过.
其中所有正确结论的序号是 .
【答案】②③④
【解析】由题中数据知,其它类营业收入占比,为最低的,故①错;
生鲜区的净利润占比,故②正确;
生鲜区的营业利润率为,故④正确;
熟食区的营业利润率为;
乳制品区的营业利润率为;
其他区的营业利润率为;
日用品区为,最高,故③正确.
故答案为:②③④.
14.(2024·高一·甘肃天水·阶段练习)如图是一个容量为200的样本的频率分布直方图,请根据图中的数据填空:
(1)样本数据落在范围的频率为 ;
(2)样本数据落在范围的频数为 .
【答案】
【解析】由频率分布直方图可得,
样本数据落在范围的频率为.
样本数据落在范围的频率为
所以样本数据落在范围的频数为.
故答案为:;.
15.(2024·高一·陕西宝鸡·阶段练习)某中学为了解高三男生的体能情况,通过随机抽样,获得了200名男生的100米体能测试成绩(单位:秒),将数据按照,,…,分成9组,制成了如图所示的频率分布直方图.由直方图估计本校高三男生100米体能测试成绩大于13.25秒的频率是 .
【答案】0.63/
【解析】由频率分布直方图中各矩形面积之和为1,
可得,
解得,
故体能测试成绩大于13.25秒的频率是,
故答案为:0.63
16.(2024·江西上饶·一模)2022年12月4日是第九个国家宪法日,主题为“学习宣传贯彻党的二十大精神,推动全面贯彻实施宪法”,某校由学生会同学制作了宪法学习问卷,收获了有效答卷2000份,先对其得分情况进行了统计,按照、、…、分成5组,并绘制了如图所示的频率分布直方图,则图中 .
【答案】0.020
【解析】由频率分布直方图的性质可得,
,
故答案为:0.020
四、解答题
17.(2024·高一·云南保山·开学考试)近几年购物的支付方式日益增多,某数学兴趣小组就此进行了抽样调查.调查结果显示,支付方式有:A微信、B支付宝、C现金、D其他,该小组对某超市一天内购买者的支付方式进行调查统计,得到如下两幅不完整的统计图.
请你根据统计图提供的信息,解答下列问题:
(1)本次一共调查了多少名购买者?
(2)请补全条形统计图;
在扇形统计图中A种支付方式所对应的圆心角为______度.
(3)若该超市这一周内有1600名购买者,请你估计使用A和B两种支付方式的购买者共有多少名?
【解析】(1),即本次一共调查了200名购买者;
(2)D方式支付的有:(人),
A方式支付的有:(人),
补全的条形统计图如图所示,
在扇形统计图中A种支付方式所对应的圆心角为:
(3)(名),
使用A和B两种支付方式的购买者共有928名.
18.(2024·高一·全国·随堂练习)下面是2003年4月21日至5月15日上午10时,北京市非典型性肺炎疫情新增数据走势图.
(1)哪一天新增确诊的人数最多?哪一天新增疑似的人数最多?
(2)哪一天新增治愈的人数最多?哪一天新增死亡的人数最少?
(3)从图中,你能预测这次北京市非典型性肺炎疫情的发展趋势吗?
【解析】(1)
由折线图得:2003年4月29日新增确诊的人数最多,2003年4月27日新增疑似的人数最多.
(2)由折线图得:
2003年5月13日一天新增治愈的人数最多,
2003年5月12日新增死亡的人数最少.
(3)从图中,预测这次北京市非典型性肺炎疫情的发展趋势为:
北京市非典型性肺炎疫情初期确诊病例和疑似病例数量快速上升,
然后确诊病例和疑似病例数量逐渐下降.
19.(2024·高一·全国·随堂练习)下面是2016年我国部分主要城市的年平均气温(单位:℃):
(1)将以上数据进行适当分组,并画出相应的频率分布直方图.
(2)以上各城市年平均气温在,,,中,哪一个范围的最多?
【解析】(1)
由题意得,频率分布表如下:
频率分布直方图如图:
(2)由图可知以上各城市年平均气温在的最多.
20.(2024·高一·全国·随堂练习)为了解一个鱼塘中养殖的鱼的生长情况,从这个鱼塘中多个不同位置捕捞出100条鱼,称得每条鱼的质量(单位:kg),并将所得数据分组(每组包含左端值,不包含右端值),画出频率分布直方图,如图所示.
(1)根据直方图作频率分布表;
(2)估计数据落在中的概率为多少;
(3)将上面捕捞的100条鱼分别做一记号后再放回鱼塘,几天后再从鱼塘的多处不同位置捕捞出120条鱼,其中带有记号的鱼有6条,请根据这一情况来估计该鱼塘中鱼的总条数.
【解析】(1)根据频率分布直方图可知,频率=组距(频率/组距),故可得下表
(2),所以数据落在中的概率约为0.47.
(3)设水库中鱼的总条数约为条,则,
即,所以水库中鱼的总条数约为2000条.
21.(2024·高一·江苏·专题练习)有一容量为50的样本,数据的分组及各组的数据如下:,4;,9;,5;,8;,10;,3;,11.
(1)列出样本频率分布表;
(2)画出频率直方图及频率折线图.
【解析】(1)由所给的数据,不难得出以下样本的频率分布表.
(2)频率直方图如图1所示,频率折线图如图2折线部分所示.
22.(2024·高一·江苏·专题练习)某校高二年级期末统一测试,随机抽取一部分学生的数学成绩,分组统计如下表.
(1)求出表中的值,并根据表中所给数据在给出的坐标系中画出频率直方图;
(2)若全校参加本次考试的学生有600人,试估计这次测试中全校成绩在90分以上的人数.
【解析】(1)由频率分布表得,
所以,,
频率直方图如图所示,
(2)由题意,知全校成绩在90分以上的学生的人数约为.
课程标准
学习目标
(1)能用总体频率分布表的频率分布直方图描述或近似描述总体的取值规律,并刻画总体各方面的统计特征.
(1)掌握频率分布表的作法以及频率直方图的画法.
(2)掌握用频率直方图估计总体.
统计图表
主要应用
扇形统计图
直观描述各类数据占总数的比例
频数直方图
反映分布状况,又可以表示变化趋势
折线统计图
描述数据随时间的变化趋势
135
98
102
110
99
121
110
96
100
103
125
97
117
113
110
92
102
109
104
112
105
124
87
131
97
102
123
104
104
128
109
123
111
103
105
92
114
108
104
102
129
126
97
100
115
111
106
117
104
109
111
89
110
121
80
120
121
104
108
118
129
99
90
99
121
123
107
111
91
100
99
101
116
97
102
108
101
95
107
101
102
108
117
99
118
106
119
97
126
108
123
119
98
121
101
113
102
103
104
108
分组
频数
频率
频率/组距
1
0.01
0.002
2
0.02
0.004
4
0.04
0.008
14
0.14
0.028
24
0.24
0.048
15
0.15
0.030
12
0.12
0.024
9
0.09
0.018
11
0.11
0.022
6
0.06
0.012
2
0.02
0.004
合计
100
1
0.2
57 46 49 54 55 58 49 61 51 49
51 60 52 54 51 55 60 56 47 47
53 51 48 53 50 52 40 45 57 53
52 51 46 48 47 53 47 53 44 47
50 52 53 47 45 48 54 52 48 46
49 52 59 53 50 43 53 46 57 49
49 44 57 52 42 49 43 47 46 48
51 59 45 45 46 52 55 47 49 50
54 47 48 44 57 47 53 58 52 48
55 53 57 49 56 56 57 53 41 48
分组
频数
频率
2
0.02
3
0.03
7
0.07
16
0.16
17
0.17
10
0.10
20
0.20
8
0.08
10
0.10
4
0.04
3
0.03
身高分段
发生次数
频率
2
2
8
11
14
9
4
总计
50
分组
频数
3
6
12
频率
0.3
分组
频数
3
6
12
21
18
频率
0.05
0.1
0.2
0.35
0.3
成绩分组(分)
频数
频率
合计
171
170
165
169
167
167
170
161
164
167
171
163
163
169
166
168
168
165
160
168
158
160
163
167
173
168
169
170
160
164
171
169
167
159
151
168
170
174
160
168
176
157
162
166
158
164
180
179
169
169
身高
频数
频率
身高
频数
频率
1
0.02
0
0
4
0.08
6
0.12
8
0.16
13
0.26
13
0.26
2
0.04
1
0.02
2
0.04
组别
数学小组
写作小组
体育小组
音乐小组
科技小组
频率
班级
(1)
(2)
(3)
优秀率
寿命/天
频数
频率
20
0.10
30
y
70
0.35
x
0.15
50
0.25
合计
200
1
生鲜区
熟食区
乳制品区
日用品区
其它区
营业收入占比
净利润占比
城市
年平均气温
城市
年平均气温
城市
年平均气温
城市
年平均气温
北京
13.8
上海
17.6
武汉
17.3
昆明
15.8
天津
13.8
南京
16.8
长沙
17.5
拉萨
9.5
石家庄
14.6
杭州
18.2
广州
21.9
西安(泾河)
15.8
太原
11.2
合肥
17.0
南宁
22.3
兰州(皋兰)
8.2
呼和浩特
7.1
福州
21.0
海口
24.6
西宁
6.6
沈阳
8.8
南昌
19.0
重庆(沙坪坝)
19.5
银川
10.7
长春
6.6
济南
15.4
成都(温江)
16.8
乌鲁木齐
8.4
哈尔滨
5.0
郑州
16.4
贵阳
15.3
温度
频数
频率
频率/组距
,
8
0.258
0.0516
5
0.161
0.0322
14
0.452
0.0904
4
0.129
0.0258
分组
频率
0.05
0.20
0.28
0.30
0.15
0.02
数据段
频数
频率
4
0.08
5
0.10
10
0.20
11
0.22
9
0.18
8
0.16
3
0.06
合计
50
1
分组
频数
频率
3
0.03
3
0.03
37
0.37
m
n
15
0.15
合计
M
N
数学必修 第二册12.1 复数的概念精品同步训练题: 这是一份数学必修 第二册<a href="/sx/tb_c4002204_t7/?tag_id=28" target="_blank">12.1 复数的概念精品同步训练题</a>,文件包含121复数的概念三大题型练习原卷高中数学苏教版必修二docx、121复数的概念三大题型练习解析卷高中数学苏教版必修二docx等2份试卷配套教学资源,其中试卷共24页, 欢迎下载使用。
高中数学苏教版 (2019)必修 第二册14.3 统计图表精品同步达标检测题: 这是一份高中数学苏教版 (2019)必修 第二册<a href="/sx/tb_c4002217_t7/?tag_id=28" target="_blank">14.3 统计图表精品同步达标检测题</a>,文件包含苏教版数学高一必修第二册143统计图表分层练习原卷版docx、苏教版数学高一必修第二册143统计图表分层练习解析版docx等2份试卷配套教学资源,其中试卷共51页, 欢迎下载使用。
苏教版 (2019)必修 第二册14.3 统计图表课后练习题: 这是一份苏教版 (2019)必修 第二册<a href="/sx/tb_c4002217_t7/?tag_id=28" target="_blank">14.3 统计图表课后练习题</a>,文件包含2023-2024学年高一数学下册同步学与练苏教版-143统计图表三大题型原卷版docx、2023-2024学年高一数学下册同步学与练苏教版-143统计图表三大题型解析版docx等2份试卷配套教学资源,其中试卷共62页, 欢迎下载使用。













