





还剩35页未读,
继续阅读
所属成套资源:全套华东师大版初中数学九年级上册素养测试+综合测试课件
成套系列资料,整套一键下载
华东师大版初中数学九年级上册第23章素养提优测试卷课件
展开
这是一份华东师大版初中数学九年级上册第23章素养提优测试卷课件,共43页。
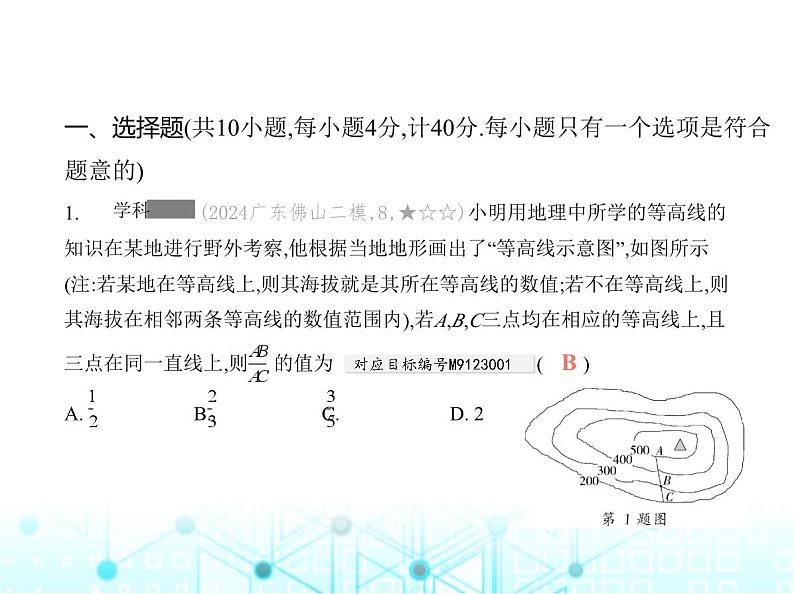
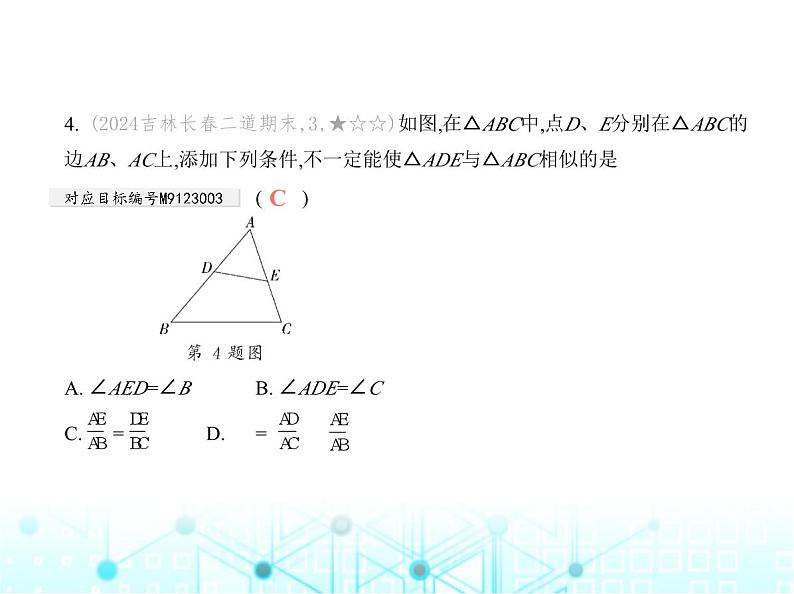
九年级 上册 第23章 素养提优测试卷(时间:90分钟 满分:120分)一、选择题(共10小题,每小题4分,计40分.每小题只有一个选项是符合题意的)1. (2024广东佛山二模,8,★☆☆)小明用地理中所学的等高线的 知识在某地进行野外考察,他根据当地地形画出了“等高线示意图”,如图所示 (注:若某地在等高线上,则其海拔就是其所在等高线的数值;若不在等高线上,则 其海拔在相邻两条等高线的数值范围内),若A,B,C三点均在相应的等高线上,且 三点在同一直线上,则 的值为 对应目标编号M9123001 ( )A. B. C. D. 2B解析 B ∵点A,B,C三点均在相应的等高线上,且三点在同一直线上,∴ = = = .2. (2022江苏常州中考,7,★☆☆)在平面直角坐标系xOy中,点A与点A1关于x轴对 称,点A与点A2关于y轴对称.已知点A1(1,2),则点A2的坐标是 对应目标编号M9123007 ( )A. (-2,1) B. (-2,-1) C. (-1,2) D. (-1,-2)D解析 D ∵点A与点A1关于x轴对称,点A1(1,2),∴点A的坐标为(1,-2),∵点A与点A2关于y轴对称,∴点A2的坐标为(-1,-2).3. (2024四川达州渠县期末,4,★☆☆)若 = = =-5,且a+c+e=20,则b+d+f值为 对应目标编号M9123001 ( )A. 10 B. 4 C. -4 D. -5C4. (2024吉林长春二道期末,3,★☆☆)如图,在△ABC中,点D、E分别在△ABC的 边AB、AC上,添加下列条件,不一定能使△ADE与△ABC相似的是 对应目标编号M9123003 ( ) A. ∠AED=∠B B. ∠ADE=∠CC. = D. = C解析 C 由题意可知∠A=∠A,当添加∠AED=∠B或∠ADE=∠C或 = 时,均可得到△ADE与△ABC相似,但当添加 = 时,不能判定△ADE与△ABC相似.5. (2023四川遂宁中考,6,★☆☆)在方格图中,以格点为顶点的三角形叫做格点三 角形.在如图所示的平面直角坐标系中,格点△ABC、△DEF成位似关系,则位似 中心的坐标为 对应目标编号M9123007 ( ) A. (-1,0) B. (0,0) C. (0,1) D. (1,0)A解析 A 如图,△ABC与△DEF的对应顶点的连线相交于点(-1,0),则位似中心 的坐标为(-1,0). 6. (2024安徽滁州定远期末,4,★☆☆)如图,在菱形ABCD中,E为CD上一点,连结 AE、BD交于点F,S△DEF∶S△ABF=4∶25,则DE∶AD= ( ) A. 3∶2 B. 2∶3 C. 2∶5 D. 3∶5C解析 C ∵四边形ABCD是菱形,∴AB∥CD,AB=AD,∴∠FAB=∠DEF,∠ABF= ∠EDF,∴△DEF∽△BAF,∵S△DEF∶S△ABF=4∶25,∴DE∶AB=2∶5,∴DE∶AD= 2∶5.7. (2024吉林长春东北师大附中月考,7,★☆☆)如图,在△ABC中,点D,E分别是边 AB,AC的中点,连结DE,BE,CD,BE与CD交于点F,则下列结论不正确的是 ( ) A. BC=2DE B. BE=3EFC. S△ABC=4S△ADE D. AB=2AED解析 D ∵点D,E分别是边AB,AC的中点,∴BC=2DE,故选项A正确;∵点D,E分 别是边AB,AC的中点,∴BC=2DE,DE∥BC,∴△BCF∽△EDF,∴ = =2,∴BE=3EF,故选项B正确;∵DE∥BC,∴△ABC∽△ADE,∴ = =4,∴S△ABC=4S△ADE,故选项C正确;∵E是AC的中点,∴AC=2AE,当AB≠AC时,AB≠2AE,故选 项D错误.8. (2023山东济南历下期中,9,★★☆)图①是小玉制作的简易投石机的示意图, GP是杠杆,点A为支点,AD=AC,支架AH垂直于地面BC,且AH=CD=2.如图②,当投 石机准备时,点G恰好与点B重合,此时AG和AC垂直,则线段AG= ( ) A. 4 B. 2 C. 6 D. 2 B解析 B ∵AD=AC,AH⊥CD,AH=CD=2,∴CH= CD= ×2=1,∠AHC=90°,∴AC= = = ,在题图②中,∵∠BAC=90°,∴∠BAC=∠AHC,∵∠ACB=∠ACH,∴△ACH∽△BCA,∴ = ,即 = ,∴AB=2 ,∴AG=2 ,故选B.9. [教材变式P98T21](2023山东威海中考,9,★★☆)如图,四边形ABCD是一张矩 形纸片.将其按如图所示的方式折叠:使DA边落在DC边上,点A落在点H处,折痕 为DE;使CB边落在CD边上,点B落在点G处,折痕为CF.若矩形HEFG与原矩形 ABCD相似,AD=1,则CD的长为 ( ) A. -1 B. -1 C. +1 D. +1C解析 C 设HG=x,∵四边形ABCD是矩形,∴∠A=∠ADH=90°,BC=AD=1,由折 叠得∠DHE=∠A=90°,DH=AD=1,CG=BC=1,∴四边形ADHE是正方形,∴HE= AD=1,∵矩形HEFG与原矩形ABCD相似,∴ = ,∴ = ,解得x= -1或x=- -1,经检验,x= -1,x=- -1都是原方程的根,∵GH>0,∴GH= -1,∴CD=2+x= +1.10. (2022四川乐山中考,10,★★☆)如图,等腰△ABC的面积为2 ,AB=AC,BC=2.作AE∥BC且AE= BC.点P是线段AB上一动点,连结PE,过点E作PE的垂线交BC的延长线于点F,M是线段EF的中点.那么,当点P从A点运动到B点时,点M的运 动路径长为 对应目标编号M9123003 ( ) A. B. 3 C. 2 D. 4B解析 B 如图,过点A作AH⊥BC于点H.当点P与A重合时,点F与C重合,当点P与 B重合时,点F的对应点为F″,易知点M的运动轨迹是线段M'M″,且M'M″= CF″.∵AB=AC,AH⊥BC,∴BH=CH,∵AE∥BC,AE= BC,∴AE=CH,∴四边形AHCE是平行四边形,∵∠AHC=90°,∴四边形AHCE是矩形,∴EC⊥BF″,AH=EC,∵BC=2,S△ABC=2 ,∴ ×2×AH=2 ,∴AH=EC=2 ,∵∠BEF″=∠ECB=∠ECF″=90°,∴∠BEC+∠CEF″=90°,∠CEF″+∠F″=90°,∴∠BEC=∠F″,∴△ECB∽△F″CE,∴ = ,即EC2=CB·CF″,∴CF″= = =6,∴M'M″= CF″=3. 二、填空题(共6小题,每小题4分,计24分)11. (2024江苏南京玄武期末,8,★☆☆)若两个相似三角形的面积之比为16∶9,则 它们对应边上的中线之比为 .4∶3解析 ∵两个相似三角形的面积之比为16∶9,∴它们对应边上的中线之比为 4∶3.12. (2023四川成都天府七中执诚学部月考,11,★☆☆)在小提琴 的设计中,经常会引入黄金分割的概念.如图,AC、BC、AB的长度满足 = ,则 = . 对应目标编号M9123001 解析 ∵点C把线段AB分成两部分且 = ,∴点C是线段AB的黄金分割点,又BC>AC,∴BC= AB,∴AC=AB-BC= AB,∴ = .13.(新独家原创,★☆☆)矩形钢板ABCD的长AD=8 cm,宽AB=6 cm,裁掉两个角 得到如图所示的五边形零件,已知AE=2 cm,EF=5 cm,FG=6.25 cm,则∠AEF+∠FGD= 度. 270解析 ∵四边形ABCD是矩形,AD=8 cm,∴∠B=∠C=90°,BC=AD=8 cm.∵AB=6cm,AE=2 cm,∴BE=4 cm.在Rt△BEF中,EF=5 cm,∴BF= = =3(cm),∴CF=BC-BF=8-3=5(cm).在△BEF和△CFG中, = , = = ,∴ = ,又∵∠B=∠C=90°,∴Rt△BEF∽Rt△CFG,∴∠BEF=∠CFG.∵∠AEF=180°-∠BEF,∠FGD=∠C+∠CFG=90°+∠BEF,∴∠AEF+∠FGD=180°-∠BEF+90°+ ∠BEF=270°.14. (2024江苏泰州二附中期中,16,★★☆)早在西汉时期, 我国天文学家就提出了一种测量日高的公式——“重差术”.如图,用长度为a的 杆子(“表”)在间距为d的两个地点测日影,测得影长分别为s1,s2,用这种方式计 算出的日高公式H= .(用含a、d、s1、s2的代数式表示) 对应目标编号M9123005 解析 如图, ∵AB⊥BG,CD⊥BG,EF⊥BG,∴AB∥CD∥EF,∴△EFG∽△ABG,△CDO∽△ABO,∴ = , = ,∴ = , = ,∴H= .15. (2024河南南阳十七中期末,16,★★☆)如图,已知点P是边长为5的正方形 ABCD内一点,且PB=2,BF⊥BP于B,若在射线BF上找一点M,使以点B,M,C为顶 点的三角形与△ABP相似,则BM的值为 . 解析 ∵四边形ABCD是边长为5的正方形,∴∠ABC=90°,AB=BC=5.∵∠PBF= 90°,∴∠ABP=∠CBF.若以点B,M,C为顶点的三角形与△ABP相似,分情况求解 如下:①当 = ,即 = 时,解得BM= ;②当 = ,即 = 时,解得BM=2.综上所述,满足条件的BM的值为2或 .16. (2023辽宁抚顺中考,17,★★☆)如图,平行四边形ABCD的对角线AC,BD相交 于点O,过点B作BE∥AC,交DA的延长线于点E,连结OE,交AB于点F,则四边形 BCOF的面积与△AEF的面积的比值为 . 对应目标编号M9123003 解析 ∵四边形ABCD是平行四边形,AD∥BC,OA=OC,∵BE∥AC,∴△OAF∽ △EBF,四边形AEBC是平行四边形,∴ = ,AC=BE,∴BE=2OA,∴ = = , =2,∴S△EBF=4S△OAF, = =2,∴S△AEF=2S△AOF,同理S△EBF=2S△OBF,S△OBC=S△OAB,设S△OAF=x,则S△EBF=4x,S△AEF=2x,∴S△OBF=2x,∴S△BOC=S△AOB=S△AOF+S△BOF=x +2x=3x,∴S四边形BCOF=S△BOC+S△BOF=3x+2x=5x,∴ = = .模型解读 相似三角形常见模型——8字模型此模型中的两个三角形有一组“对顶角”,只需再找一对等角或夹这组对顶角 的两边成比例,就可说明这两个三角形相似.三、解答题(共5小题,计56分)17. (2024吉林长春宽城期中,21,★☆☆)(8分)如图,在△ABC中,M、N分别是 AB、AC的中点,连结MN,点E是线段CN的中点,连结ME并延长交BC的延长线 于点D,若BC=10,求CD的长. 对应目标编号M9123005 解析 ∵M、N分别是AB、AC的中点,∴MN是△ABC的中位线,∴MN∥BC, MN= BC= ×10=5,∴△MEN∽△DEC,∴ = ,又∵点E是CN的中点,∴CD=MN=5.18. (2024江西宜春宣化期末,15,★☆☆)(12分)如图,已知Rt△ABC,∠ABC=90°, 点A在y轴上,点B在x轴上,AB=10,BC=5,点C(m,3). 对应目标编号M9123006(1)求点A、B的坐标及m的值.(2)在第一象限内,画出以原点O为位似中心,将△ABC缩小后所得的△DEF,使△DEF与△ABC的对应边之比为1∶2. 解析 (1)如图,过点C作CM⊥x轴于点M,∵∠ABC=90°,∴∠ABO+∠CBM=90°,∵∠CBM+∠BCM=90°,∴∠ABO=∠BCM,∵∠AOB=∠CMB,∴△AOB∽△BMC,∴ = = =2,∴BO=6,∴AO= =8,∴BM= AO=4,故m=4+6=10.综上,A(0,8),B(6,0),m的值为10. (2)如图所示,△DEF即为所求.19. (2022陕西咸阳兴平模拟,22,★★☆)(10分)一个阳光明媚的午后,小丽和小明 准备测量千金塔的高度(塔的顶部A不易到达,底部B可以到达),他们所带的测量 工具有:①可调节高度的标杆,②皮尺,③自制三角板(角度未知).请你用学过的知 识设计一种测量塔高的方案.(1)你所选用的测量工具是 .(填序号)(2)画出测量示意图,并用a、b、c等字母表示出测量数据.(不要求写操作步骤)(3)结合测量数据,用含a、b、c等字母的式子表示出千金塔的高度. 解析 (1)①②.(2)测量示意图如下.(3)如图,设AB=x米,测得标杆DE=a米,千金塔和标杆的影长分别为b米,c米,∵△DEF∽△ABC,∴ = ,20. (2024吉林长春双阳期末,20,★★☆)(12分)图①、图②、图③均是6×5的正方 形网格,每个小正方形的顶点称为格点,且每个小正方形的边长均为1,点A、B、 C、D、F、G、K、M、H、N均在格点上.在给定的网格中画图或填空,要求只 用无刻度的直尺,保留作图痕迹,不要求写出画法. 对应目标编号M9123003(1)图①中, 的值为 .(2)如图②,在FG上找一点P,使FP=3.(3)如图③,在KM上找一点Q,连结HQ、NQ,使△HKQ∽△NMQ. 解析 (1)∵DC∥AB,DC=3,AB=2,∴△DEC∽△AEB,∴ = = ,∴ 的值为 .(2)如图1,取格点L、J,连结LJ交FG于点P,点P即为所求.详解:连结LF、JG,∵FG= =5,LF∥JG,∴△LFP∽△JGP,∴ = = ,∴FP= FG= ×5=3,∴点P即为所求. (3)如图2,取格点Q,连结QH、QN,点Q及△HKQ、△NMQ即为所求.(答案不唯一)详解:∵KH=KQ=3,MN=MQ=2,∴ = = ,∵∠HKQ=∠NMQ=90°,∴△HKQ∽△NMQ,∴点Q及△HKQ、△NMQ即为所 求.21. (2024福建漳州龙文二模,26,★★★)(14分)如图①,在△ABC中,∠ACB=90°, 以AB为斜边作等腰直角△ABD,点E在BC上,且BE=AC,连结DC、DE.(1)求证:△ACD≌△BED.(2)如图②,延长DC、BA交于点G,求证:DB2=DE·DG.(3)如图③,过点E作CG的平行线交BG于点H,若BE=1,CG=2,求EH的长. 解析 (1)证明:∵△ABD是等腰直角三角形,∴∠DAB=∠DBA=45°,∴∠DBE= ∠ABD-∠ABC=45°-∠ABC,∵∠ACB=90°,∴∠CAD=90°-∠DAB-∠ABC=90°-45°-∠ABC=45°-∠ABC,∴∠CAD=∠EBD,∵AD=BD,AC=BE,∴△ACD≌△BED.(2)证明:由(1)知△ACD≌△BED,∴CD=ED,∠ADC=∠BDE,∴∠CDA+∠ADE= ∠ADE+∠BDE=90°,∴∠CDE=90°,∴△CDE是等腰直角三角形,∴∠DCE=∠DEC=45°,∵∠DCE=∠G+∠CBG=45°,∠ABD=∠ABC+∠DBE=45°,∴∠G=∠DBE,∴△AGD∽△EBD,∴ = .∵BD=AD,∴DB2=DE·DG.(3)∵EH∥DG,∴ = ,∴ = ,∴EH= .设DC=DE=x,则CE= x,BC= x+1,∵AD2=DB2=DE·DG=x(2+x),∴AB2=2DB2=2x(2+x),∵∠ACB=90°,∴AB2=AC2+BC2,∵△ACD≌△BED,∴AC=BE=1,∴2x(2+x)=12+( x+1)2,解得x= ,∴BC= +1= +2,∴EH= = =2- .
九年级 上册 第23章 素养提优测试卷(时间:90分钟 满分:120分)一、选择题(共10小题,每小题4分,计40分.每小题只有一个选项是符合题意的)1. (2024广东佛山二模,8,★☆☆)小明用地理中所学的等高线的 知识在某地进行野外考察,他根据当地地形画出了“等高线示意图”,如图所示 (注:若某地在等高线上,则其海拔就是其所在等高线的数值;若不在等高线上,则 其海拔在相邻两条等高线的数值范围内),若A,B,C三点均在相应的等高线上,且 三点在同一直线上,则 的值为 对应目标编号M9123001 ( )A. B. C. D. 2B解析 B ∵点A,B,C三点均在相应的等高线上,且三点在同一直线上,∴ = = = .2. (2022江苏常州中考,7,★☆☆)在平面直角坐标系xOy中,点A与点A1关于x轴对 称,点A与点A2关于y轴对称.已知点A1(1,2),则点A2的坐标是 对应目标编号M9123007 ( )A. (-2,1) B. (-2,-1) C. (-1,2) D. (-1,-2)D解析 D ∵点A与点A1关于x轴对称,点A1(1,2),∴点A的坐标为(1,-2),∵点A与点A2关于y轴对称,∴点A2的坐标为(-1,-2).3. (2024四川达州渠县期末,4,★☆☆)若 = = =-5,且a+c+e=20,则b+d+f值为 对应目标编号M9123001 ( )A. 10 B. 4 C. -4 D. -5C4. (2024吉林长春二道期末,3,★☆☆)如图,在△ABC中,点D、E分别在△ABC的 边AB、AC上,添加下列条件,不一定能使△ADE与△ABC相似的是 对应目标编号M9123003 ( ) A. ∠AED=∠B B. ∠ADE=∠CC. = D. = C解析 C 由题意可知∠A=∠A,当添加∠AED=∠B或∠ADE=∠C或 = 时,均可得到△ADE与△ABC相似,但当添加 = 时,不能判定△ADE与△ABC相似.5. (2023四川遂宁中考,6,★☆☆)在方格图中,以格点为顶点的三角形叫做格点三 角形.在如图所示的平面直角坐标系中,格点△ABC、△DEF成位似关系,则位似 中心的坐标为 对应目标编号M9123007 ( ) A. (-1,0) B. (0,0) C. (0,1) D. (1,0)A解析 A 如图,△ABC与△DEF的对应顶点的连线相交于点(-1,0),则位似中心 的坐标为(-1,0). 6. (2024安徽滁州定远期末,4,★☆☆)如图,在菱形ABCD中,E为CD上一点,连结 AE、BD交于点F,S△DEF∶S△ABF=4∶25,则DE∶AD= ( ) A. 3∶2 B. 2∶3 C. 2∶5 D. 3∶5C解析 C ∵四边形ABCD是菱形,∴AB∥CD,AB=AD,∴∠FAB=∠DEF,∠ABF= ∠EDF,∴△DEF∽△BAF,∵S△DEF∶S△ABF=4∶25,∴DE∶AB=2∶5,∴DE∶AD= 2∶5.7. (2024吉林长春东北师大附中月考,7,★☆☆)如图,在△ABC中,点D,E分别是边 AB,AC的中点,连结DE,BE,CD,BE与CD交于点F,则下列结论不正确的是 ( ) A. BC=2DE B. BE=3EFC. S△ABC=4S△ADE D. AB=2AED解析 D ∵点D,E分别是边AB,AC的中点,∴BC=2DE,故选项A正确;∵点D,E分 别是边AB,AC的中点,∴BC=2DE,DE∥BC,∴△BCF∽△EDF,∴ = =2,∴BE=3EF,故选项B正确;∵DE∥BC,∴△ABC∽△ADE,∴ = =4,∴S△ABC=4S△ADE,故选项C正确;∵E是AC的中点,∴AC=2AE,当AB≠AC时,AB≠2AE,故选 项D错误.8. (2023山东济南历下期中,9,★★☆)图①是小玉制作的简易投石机的示意图, GP是杠杆,点A为支点,AD=AC,支架AH垂直于地面BC,且AH=CD=2.如图②,当投 石机准备时,点G恰好与点B重合,此时AG和AC垂直,则线段AG= ( ) A. 4 B. 2 C. 6 D. 2 B解析 B ∵AD=AC,AH⊥CD,AH=CD=2,∴CH= CD= ×2=1,∠AHC=90°,∴AC= = = ,在题图②中,∵∠BAC=90°,∴∠BAC=∠AHC,∵∠ACB=∠ACH,∴△ACH∽△BCA,∴ = ,即 = ,∴AB=2 ,∴AG=2 ,故选B.9. [教材变式P98T21](2023山东威海中考,9,★★☆)如图,四边形ABCD是一张矩 形纸片.将其按如图所示的方式折叠:使DA边落在DC边上,点A落在点H处,折痕 为DE;使CB边落在CD边上,点B落在点G处,折痕为CF.若矩形HEFG与原矩形 ABCD相似,AD=1,则CD的长为 ( ) A. -1 B. -1 C. +1 D. +1C解析 C 设HG=x,∵四边形ABCD是矩形,∴∠A=∠ADH=90°,BC=AD=1,由折 叠得∠DHE=∠A=90°,DH=AD=1,CG=BC=1,∴四边形ADHE是正方形,∴HE= AD=1,∵矩形HEFG与原矩形ABCD相似,∴ = ,∴ = ,解得x= -1或x=- -1,经检验,x= -1,x=- -1都是原方程的根,∵GH>0,∴GH= -1,∴CD=2+x= +1.10. (2022四川乐山中考,10,★★☆)如图,等腰△ABC的面积为2 ,AB=AC,BC=2.作AE∥BC且AE= BC.点P是线段AB上一动点,连结PE,过点E作PE的垂线交BC的延长线于点F,M是线段EF的中点.那么,当点P从A点运动到B点时,点M的运 动路径长为 对应目标编号M9123003 ( ) A. B. 3 C. 2 D. 4B解析 B 如图,过点A作AH⊥BC于点H.当点P与A重合时,点F与C重合,当点P与 B重合时,点F的对应点为F″,易知点M的运动轨迹是线段M'M″,且M'M″= CF″.∵AB=AC,AH⊥BC,∴BH=CH,∵AE∥BC,AE= BC,∴AE=CH,∴四边形AHCE是平行四边形,∵∠AHC=90°,∴四边形AHCE是矩形,∴EC⊥BF″,AH=EC,∵BC=2,S△ABC=2 ,∴ ×2×AH=2 ,∴AH=EC=2 ,∵∠BEF″=∠ECB=∠ECF″=90°,∴∠BEC+∠CEF″=90°,∠CEF″+∠F″=90°,∴∠BEC=∠F″,∴△ECB∽△F″CE,∴ = ,即EC2=CB·CF″,∴CF″= = =6,∴M'M″= CF″=3. 二、填空题(共6小题,每小题4分,计24分)11. (2024江苏南京玄武期末,8,★☆☆)若两个相似三角形的面积之比为16∶9,则 它们对应边上的中线之比为 .4∶3解析 ∵两个相似三角形的面积之比为16∶9,∴它们对应边上的中线之比为 4∶3.12. (2023四川成都天府七中执诚学部月考,11,★☆☆)在小提琴 的设计中,经常会引入黄金分割的概念.如图,AC、BC、AB的长度满足 = ,则 = . 对应目标编号M9123001 解析 ∵点C把线段AB分成两部分且 = ,∴点C是线段AB的黄金分割点,又BC>AC,∴BC= AB,∴AC=AB-BC= AB,∴ = .13.(新独家原创,★☆☆)矩形钢板ABCD的长AD=8 cm,宽AB=6 cm,裁掉两个角 得到如图所示的五边形零件,已知AE=2 cm,EF=5 cm,FG=6.25 cm,则∠AEF+∠FGD= 度. 270解析 ∵四边形ABCD是矩形,AD=8 cm,∴∠B=∠C=90°,BC=AD=8 cm.∵AB=6cm,AE=2 cm,∴BE=4 cm.在Rt△BEF中,EF=5 cm,∴BF= = =3(cm),∴CF=BC-BF=8-3=5(cm).在△BEF和△CFG中, = , = = ,∴ = ,又∵∠B=∠C=90°,∴Rt△BEF∽Rt△CFG,∴∠BEF=∠CFG.∵∠AEF=180°-∠BEF,∠FGD=∠C+∠CFG=90°+∠BEF,∴∠AEF+∠FGD=180°-∠BEF+90°+ ∠BEF=270°.14. (2024江苏泰州二附中期中,16,★★☆)早在西汉时期, 我国天文学家就提出了一种测量日高的公式——“重差术”.如图,用长度为a的 杆子(“表”)在间距为d的两个地点测日影,测得影长分别为s1,s2,用这种方式计 算出的日高公式H= .(用含a、d、s1、s2的代数式表示) 对应目标编号M9123005 解析 如图, ∵AB⊥BG,CD⊥BG,EF⊥BG,∴AB∥CD∥EF,∴△EFG∽△ABG,△CDO∽△ABO,∴ = , = ,∴ = , = ,∴H= .15. (2024河南南阳十七中期末,16,★★☆)如图,已知点P是边长为5的正方形 ABCD内一点,且PB=2,BF⊥BP于B,若在射线BF上找一点M,使以点B,M,C为顶 点的三角形与△ABP相似,则BM的值为 . 解析 ∵四边形ABCD是边长为5的正方形,∴∠ABC=90°,AB=BC=5.∵∠PBF= 90°,∴∠ABP=∠CBF.若以点B,M,C为顶点的三角形与△ABP相似,分情况求解 如下:①当 = ,即 = 时,解得BM= ;②当 = ,即 = 时,解得BM=2.综上所述,满足条件的BM的值为2或 .16. (2023辽宁抚顺中考,17,★★☆)如图,平行四边形ABCD的对角线AC,BD相交 于点O,过点B作BE∥AC,交DA的延长线于点E,连结OE,交AB于点F,则四边形 BCOF的面积与△AEF的面积的比值为 . 对应目标编号M9123003 解析 ∵四边形ABCD是平行四边形,AD∥BC,OA=OC,∵BE∥AC,∴△OAF∽ △EBF,四边形AEBC是平行四边形,∴ = ,AC=BE,∴BE=2OA,∴ = = , =2,∴S△EBF=4S△OAF, = =2,∴S△AEF=2S△AOF,同理S△EBF=2S△OBF,S△OBC=S△OAB,设S△OAF=x,则S△EBF=4x,S△AEF=2x,∴S△OBF=2x,∴S△BOC=S△AOB=S△AOF+S△BOF=x +2x=3x,∴S四边形BCOF=S△BOC+S△BOF=3x+2x=5x,∴ = = .模型解读 相似三角形常见模型——8字模型此模型中的两个三角形有一组“对顶角”,只需再找一对等角或夹这组对顶角 的两边成比例,就可说明这两个三角形相似.三、解答题(共5小题,计56分)17. (2024吉林长春宽城期中,21,★☆☆)(8分)如图,在△ABC中,M、N分别是 AB、AC的中点,连结MN,点E是线段CN的中点,连结ME并延长交BC的延长线 于点D,若BC=10,求CD的长. 对应目标编号M9123005 解析 ∵M、N分别是AB、AC的中点,∴MN是△ABC的中位线,∴MN∥BC, MN= BC= ×10=5,∴△MEN∽△DEC,∴ = ,又∵点E是CN的中点,∴CD=MN=5.18. (2024江西宜春宣化期末,15,★☆☆)(12分)如图,已知Rt△ABC,∠ABC=90°, 点A在y轴上,点B在x轴上,AB=10,BC=5,点C(m,3). 对应目标编号M9123006(1)求点A、B的坐标及m的值.(2)在第一象限内,画出以原点O为位似中心,将△ABC缩小后所得的△DEF,使△DEF与△ABC的对应边之比为1∶2. 解析 (1)如图,过点C作CM⊥x轴于点M,∵∠ABC=90°,∴∠ABO+∠CBM=90°,∵∠CBM+∠BCM=90°,∴∠ABO=∠BCM,∵∠AOB=∠CMB,∴△AOB∽△BMC,∴ = = =2,∴BO=6,∴AO= =8,∴BM= AO=4,故m=4+6=10.综上,A(0,8),B(6,0),m的值为10. (2)如图所示,△DEF即为所求.19. (2022陕西咸阳兴平模拟,22,★★☆)(10分)一个阳光明媚的午后,小丽和小明 准备测量千金塔的高度(塔的顶部A不易到达,底部B可以到达),他们所带的测量 工具有:①可调节高度的标杆,②皮尺,③自制三角板(角度未知).请你用学过的知 识设计一种测量塔高的方案.(1)你所选用的测量工具是 .(填序号)(2)画出测量示意图,并用a、b、c等字母表示出测量数据.(不要求写操作步骤)(3)结合测量数据,用含a、b、c等字母的式子表示出千金塔的高度. 解析 (1)①②.(2)测量示意图如下.(3)如图,设AB=x米,测得标杆DE=a米,千金塔和标杆的影长分别为b米,c米,∵△DEF∽△ABC,∴ = ,20. (2024吉林长春双阳期末,20,★★☆)(12分)图①、图②、图③均是6×5的正方 形网格,每个小正方形的顶点称为格点,且每个小正方形的边长均为1,点A、B、 C、D、F、G、K、M、H、N均在格点上.在给定的网格中画图或填空,要求只 用无刻度的直尺,保留作图痕迹,不要求写出画法. 对应目标编号M9123003(1)图①中, 的值为 .(2)如图②,在FG上找一点P,使FP=3.(3)如图③,在KM上找一点Q,连结HQ、NQ,使△HKQ∽△NMQ. 解析 (1)∵DC∥AB,DC=3,AB=2,∴△DEC∽△AEB,∴ = = ,∴ 的值为 .(2)如图1,取格点L、J,连结LJ交FG于点P,点P即为所求.详解:连结LF、JG,∵FG= =5,LF∥JG,∴△LFP∽△JGP,∴ = = ,∴FP= FG= ×5=3,∴点P即为所求. (3)如图2,取格点Q,连结QH、QN,点Q及△HKQ、△NMQ即为所求.(答案不唯一)详解:∵KH=KQ=3,MN=MQ=2,∴ = = ,∵∠HKQ=∠NMQ=90°,∴△HKQ∽△NMQ,∴点Q及△HKQ、△NMQ即为所 求.21. (2024福建漳州龙文二模,26,★★★)(14分)如图①,在△ABC中,∠ACB=90°, 以AB为斜边作等腰直角△ABD,点E在BC上,且BE=AC,连结DC、DE.(1)求证:△ACD≌△BED.(2)如图②,延长DC、BA交于点G,求证:DB2=DE·DG.(3)如图③,过点E作CG的平行线交BG于点H,若BE=1,CG=2,求EH的长. 解析 (1)证明:∵△ABD是等腰直角三角形,∴∠DAB=∠DBA=45°,∴∠DBE= ∠ABD-∠ABC=45°-∠ABC,∵∠ACB=90°,∴∠CAD=90°-∠DAB-∠ABC=90°-45°-∠ABC=45°-∠ABC,∴∠CAD=∠EBD,∵AD=BD,AC=BE,∴△ACD≌△BED.(2)证明:由(1)知△ACD≌△BED,∴CD=ED,∠ADC=∠BDE,∴∠CDA+∠ADE= ∠ADE+∠BDE=90°,∴∠CDE=90°,∴△CDE是等腰直角三角形,∴∠DCE=∠DEC=45°,∵∠DCE=∠G+∠CBG=45°,∠ABD=∠ABC+∠DBE=45°,∴∠G=∠DBE,∴△AGD∽△EBD,∴ = .∵BD=AD,∴DB2=DE·DG.(3)∵EH∥DG,∴ = ,∴ = ,∴EH= .设DC=DE=x,则CE= x,BC= x+1,∵AD2=DB2=DE·DG=x(2+x),∴AB2=2DB2=2x(2+x),∵∠ACB=90°,∴AB2=AC2+BC2,∵△ACD≌△BED,∴AC=BE=1,∴2x(2+x)=12+( x+1)2,解得x= ,∴BC= +1= +2,∴EH= = =2- .
相关资料
更多









