




人教A版 (2019)必修 第一册4.2 指数函数优秀习题
展开TOC \ "1-3" \h \z \t "正文,1"
\l "_Tc118317572" 【考点1:指数函数的概念】 PAGEREF _Tc118317572 \h 1
\l "_Tc118317573" 【考点2:指数函数的图象】 PAGEREF _Tc118317573 \h 3
\l "_Tc118317574" 【考点3:指数函数的定义域与值域】 PAGEREF _Tc118317574 \h 9
\l "_Tc118317575" 【考点4:指数函数的单调性与最值】 PAGEREF _Tc118317575 \h 14
\l "_Tc118317576" 【考点5:指数函数的应用】 PAGEREF _Tc118317576 \h 15
【考点1:指数函数的概念】
【知识点:指数函数的概念】
形如y=ax(a>0,且a≠1)的函数为指数函数.
1.(2023·全国·高一专题练习)若指数函数的图象过点,则的解析式为( )
A.B.C.D.
【答案】D
【分析】设出解析式,将点代入,求出解析式.
【详解】设(且),则,
解得,故.
故选:D
2.(2023·上海·高一专题练习)若函数是指数函数,则等于( )
A.或B.C.D.
【答案】C
【分析】根据指数函数的定义求解即可.
【详解】因为函数是指数函数,
所以.
故选:C
3.(多选题)(2023·全国·高一专题练习)下列函数中,不是指数函数的为( )
A.B.C.D.
【答案】BCD
【分析】根据指数函数的定义即可判断.
【详解】对于A,中底数,指数是自变量,指数式的系数为,所以是指数函数,故A不合题意;
对于B,中指数不是自变量,所以不是指数函数,故B符合题意;
对于C,中底数必须满足且时,才是指数函数,故C符合题意;
对于D,中指数式的系数不为1,所以不是指数函数,故D符合题意,
故选:BCD.
4.(2023秋·新疆阿克苏·高一校考阶段练习)若指数函数的图像经过点,则的值为 .
【答案】/
【分析】根据已知求出指数函数的解析式,从而代入即可得解.
【详解】依题意,设,
因为的图像经过点,所以,即,
所以,
所以.
故答案为:.
5.(2023·全国·高一专题练习)若指数函数的图象经过点,则 .
【答案】/
【分析】采用待定系数法,结合指数函数所过点可求得函数解析式,代入即可.
【详解】设指数函数且,
过点,,解得:,,
.
故答案为:.
6.(2023·全国·高一专题练习)若函数,且是指数函数,则 , .
【答案】
【分析】根据指数函数的定义,指数式的系数为1,常数项为0,即可求出参数的值.
【详解】因为是指数函数,
所以,解得,
故答案为:4,4.
7.(2023·全国·高一课堂例题)已知指数函数的图象经过点,求和.
【答案】,.
【分析】将代入指数函数表达式中可得,进入代入即可求解.
【详解】因为且的图象经过点,所以,
解得(负根舍去),于是.
所以,.
8.(2023·全国·高一专题练习)已知函数的图像经过点,其中且,求a的值;
【答案】
【分析】将点代入函数解析式即可求出.
【详解】由题意得,所以.
【考点2:指数函数的图象】
【知识点:指数函数的图象】
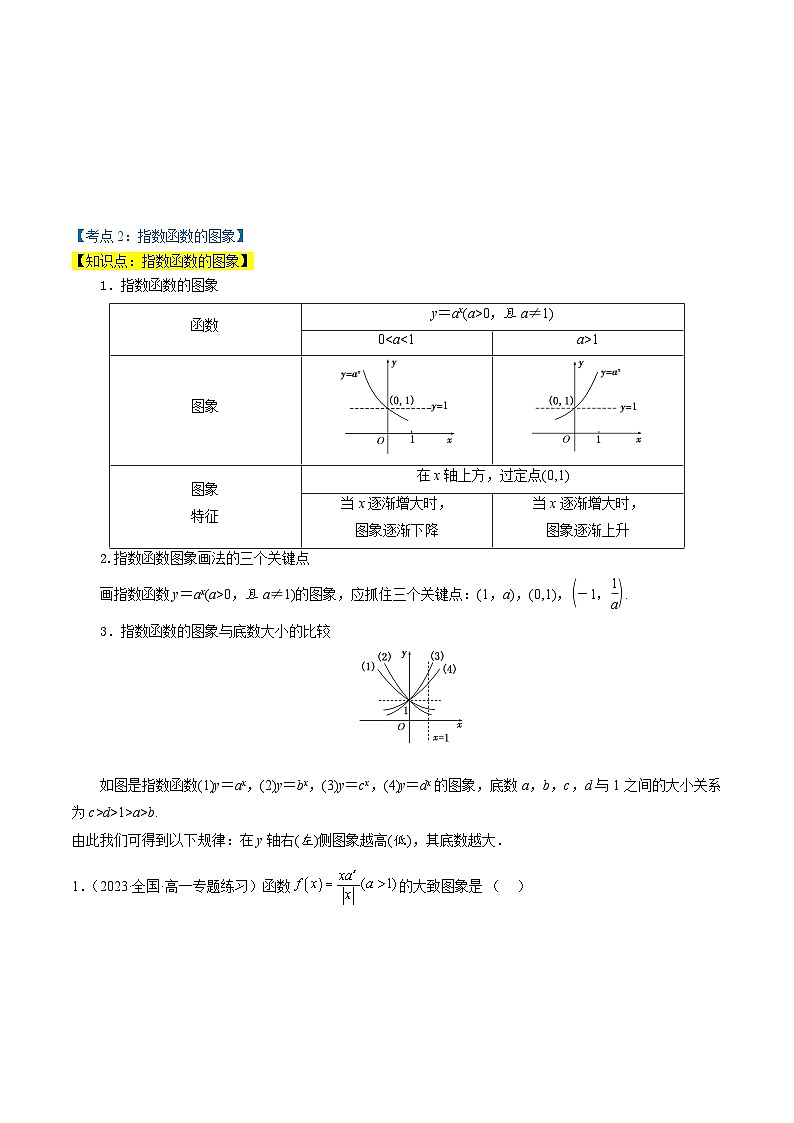
1.指数函数的图象
2.指数函数图象画法的三个关键点
画指数函数y=ax(a>0,且a≠1)的图象,应抓住三个关键点:(1,a),(0,1),eq \b\lc\(\rc\)(\a\vs4\al\c1(-1,\f(1,a))).
3.指数函数的图象与底数大小的比较
如图是指数函数(1)y=ax,(2)y=bx,(3)y=cx,(4)y=dx的图象,底数a,b,c,d与1之间的大小关系为c>d>1>a>b.
由此我们可得到以下规律:在y轴右(左)侧图象越高(低),其底数越大.
1.(2023·全国·高一专题练习)函数的大致图象是( )
A. B.
C. D.
【答案】C
【分析】先分类讨论化简函数式,然后根据指数函数的单调性排除错误选项.
【详解】因为
又,
根据指数函数的性质知,时,函数为增函数,排除B、D;
时,函数为减函数,排除A.
故选:C.
2.(2023·福建·高考模拟)函数的图象如图所示,其中a,b为常数,则下列结论正确的是( )
A.B.
C.D.
【答案】D
【分析】由函数单调性判断与的大小,再由图象与轴的交点位置判断的正负.
【详解】由图象可知,函数为减函数,
从而有;
法一:由图象,函数与轴的交点纵坐标,
令,得,
由,即,解得 .
法二:函数图象可看作是由向左平移得到的,
则,即.
故选:D.
3.(2023秋·重庆渝中·高三重庆巴蜀中学校考阶段练习)已知函数(,)恒过定点,则函数的图象不经过( )
A.第一象限B.第二象限C.第三象限D.第四象限
【答案】D
【分析】利用指数函数的性质求解.
【详解】∵,∴恒过定点,
∴,,∴,其图象不经过第四象限,
故选:D.
4.(多选)(2023秋·河北石家庄·高三石家庄市第二十五中学校考阶段练习)已知,则函数的图象可能是( )
A. B.
C. D.
【答案】AD
【分析】通过特值法,排除错误选项,通过的取值,判断函数的图象的形状,推出结果即可.
【详解】由于当时,,排除B,C,
当时,,此时函数图象对应的图形可能为A,
当时,,此时函数图象对应的的图形可能为D.
故选:AD.
5.(多选)(2023·全国·高一专题练习)已知函数,且,则下列式子可能成立的是( )
A.B.
C.D.
【答案】BCD
【分析】在同一直角坐标系中作出和的图象,然后根据图象即可完成判断.
【详解】在同一直角坐标系中作出和的图象以及平行于x轴的直线如下:
则时,的关系有三种可能,分别是:,,.
故选:BCD
6.(多选)(2023·全国·高一专题练习)(多选)已知函数(且)的图象如图所示,则下列结论正确的是( )
A.B.C.D.
【答案】ABD
【分析】根据函数图象可得出、的取值范围,利用指数函数的基本性质可判断ACD选项,利用不等式的基本性质可判断B选项.
【详解】由图象可知,函数(且)在上单调递增,则,
且当时,,可得.
对于A选项,,A对;
对于B选项,,B对;
对于C选项,,C错;
对于D选项,由题意可知,,则,所以,,D对.
故选:ABD.
7.(2023·上海·高一专题练习)函数且的图象必经过点 .
【答案】
【分析】根据指数运算的性质进行求解即可.
【详解】因为当时,,
所以函数且的图象必经过点,
故答案为:
8.(2023·全国·高一课堂例题)作出指数函数和的图象.
【答案】答案见解析
【分析】通过列表、描点连线(也可借助信息技术在计算机上作图)作图即可.
【详解】过列表、描点连线(也可借助信息技术在计算机上作图),得图4.2-3.
9.(2023·全国·高一专题练习)设a,b为实数,,.已知函数的图象如图所示,求a,b的取值范围.
【答案】a,b的取值范围分别为
【分析】从图象获取关键信息即可求解.
【详解】由题图可知函数单调递增,即,
所以的取值范围为;
由图可知当时,有,解得,
所以的取值范围为.
【考点3:指数函数的定义域与值域】
【知识点:指数函数的定义域与值域】
1.(2022秋·高一单元测试)y=2x-1的定义域是( )
A.(-∞,+∞)B.(1,+∞)
C.[1,+∞)D.(0,1)∪(1,+∞)
【答案】A
【分析】根据实数指数幂的意义可得解.
【详解】因为,
所以,
故选:A
2.(2023秋·陕西咸阳·高三校考阶段练习)若函数(且)在区间上的值域为,则实数的值为( )
A.B.2C.3D.
【答案】B
【分析】分与两种情况,结合函数单调性得到方程组,求出答案.
【详解】①当时,单调递增,
故,解得;
②当时,单调递减,
,无解,
综上可知.
故选:B
3.(2023·全国·高一专题练习)已知的值域为,则x的取值范围可以为( )
A.B.C.D.
【答案】D
【分析】令,根据值域解不等式组可得t的范围,然后解指数不等式可得.
【详解】令,则,
由题知,,解得或,
即或,解得或.
故选:D
4.(2023·全国·高一专题练习)已知函数的值域为R,则实数a的取值范围是( )
A.B.C.D.
【答案】D
【分析】由于当时,,所以当时,求出的最小值,使其最小值小于等于1即可.
【详解】当时,,
当时, ,
因为函数的值域为,
所以,得,
所以实数的取值范围是,
故选:D.
5.(2023秋·上海普陀·高一曹杨二中校考阶段练习)函数的定义域为 .
【答案】
【分析】根据二次根式的定义进行求解即可.
【详解】由,可得,所以函数的定义域为,
故答案为:
6.(2023·全国·高三专题练习)若时,指数函数的值总大于1,则实数的取值范围是 .
【答案】或
【分析】根据指数函数的性质以及单调性,即可得到关于的不等式,求解不等式即可得到结果.
【详解】由已知可得,且.
又时,,
即 ,
所以有,即,
解得或.
故答案为:或.
7.(2023秋·河北石家庄·高三石家庄市第二十五中学校考阶段练习)已知函数,求的值域 .
【答案】
【分析】根据函数的解析式,分段求每部分的值域,再求并集.
【详解】由,,则, 当时,即时,等号成立,
当时,,
综上可知,所以函数的值域是.
故答案为:
8.(2023·全国·高一专题练习)已知函数的值域为,则实数的取值范围是 .
【答案】
【分析】分别讨论当时,的值域和当时,的值域,根据分段函数的值域取二者的并集,结合集合的并集运算即可求解.
【详解】当时,在上单调递增,
所以时,;
当时,,
①若,则在上单调递增,在上单调递减,
则时,,即时,,
又时,,
此时,函数的值域为,不满足题意,舍去;
②当时,函数此时值域为,不满足题意,舍去;
③当时,在上单调递减,
则时,,即时,,
因为函数的值域为,
又时,;
则时,且,
不等式解得:,
不等式等价于时,,
设(),
因为在上单调递增,在上是增函数,
所以在上单调递增,又,
所以时,等价于,即,
则不等式解得:,
所以时,的解集为,
综上:实数的取值范围是,
故答案为:.
9.(2023·全国·高一专题练习)求下列函数的定义域和值域:
(1);
(2).
【答案】(1)定义域为;值域为
(2)定义域为;值域为
【分析】(1)根据二次根式和指数函数的性质进行求解即可;
(2)根据指数函数的性质进行求解即可.
【详解】(1)要使函数式有意义,则,即.
因为函数在上是增函数,所以.
故函数的定义域为,
因为,所以,所以,
所以,即函数的值域为;
(2)定义域为,
因为,
所以,
又,所以函数的值域为.
10.(2023秋·高一课时练习)已知函数的图象经过点,其中且.
(1)求a的值;
(2)求函数的值域.
【答案】(1)
(2).
【分析】(1)把给定的点代入函数式求出a值作答.
(2)由(1)求出函数式,再借助单调性求出值域作答.
【详解】(1)由函数的图象经过点,得,而且,
所以.
(2)由(1)知,,显然函数在上单调递减,
则当时,,且恒成立,
因此当时,函数,
所以函数的值域是.
【考点4:指数函数的单调性与最值】
【知识点:指数函数的单调性与最值】
(1)比较大小问题:常化为同底或同指,利用指数函数的单调性,图象或1,0等中间量进行比较.
(2)简单的指数方程或不等式的求解问题:解决此类问题应利用指数函数的单调性,要特别注意底数a的取值范围,并在必要时进行分类讨论.
1.(2023秋·河北唐山·高一唐山市第二中学校考阶段练习)下列函数中,在区间上单调递减的是( )
A.B.
C.D.
【答案】C
【分析】根据指数函数、幂函数等的性质判断区间单调性即可.
【详解】A:由幂函数性质知:在上单调递增,不符合;
B:由,在上单调递增,不符合;
C:由指数函数单调性知:在上单调递减,符合;
D:由,在上不单调,不符合;
故选:C
2.(2023·全国·高一专题练习)设函数在区间上单调递减,则a的取值范围是( )
A.B.C.D.
【答案】A
【分析】设,则是上的增函数,再利用复合函数的单调性求解.
【详解】解:设,对称轴为,
∵是上的增函数,
∴要使在区间单调递减,
则在区间单调递减,
即,
故实数a的取值范围是.
故选:A.
3.(2023·上海·高一专题练习)已知函数在区间上单调递减,则的取值范围是( )
A.B.
C.D.
【答案】A
【分析】由复合函数的单调性分析可知,内层函数在上为增函数,结合二次函数的单调性可得出关于实数的不等式,解之即可.
【详解】令,则二次函数的图象开口向上,对称轴为直线,
因为外层函数为上的减函数,函数在区间上单调递减,
所以,函数在上为增函数,所以,,解得.
故选:A.
4.(多选)(2023·全国·高一专题练习)已知函数,则( )
A.函数的定义域为R
B.函数的值域为
C.函数在上单调递增
D.函数在上单调递减
【答案】ABD
【分析】由函数的表达式可得函数的定义域可判断A;令,则,,结合指数函数的单调性得到函数的值域,可判断B;根据复合函数单调性的判断方法可得函数的单调性可判断C、D.
【详解】令,则,
对于选项A:的定义域与的定义域相同,均为R,故A正确;
对于选项B:因为,的值域为,
所以函数的值域为,故B正确;
对于选项C、D:因为在上单调递增,且,在定义域上单调递减,
所以根据复合函数单调性法则,得函数在上单调递减,
所以C不正确,D正确.
故选:ABD.
5.(2023春·河北石家庄·高一校考期中)已知函数在区间上的最大值比最小值大,则a=
【答案】或
【分析】分与两种情况,求出最值,列出方程,得到答案.
【详解】当时,在上的最大值为,最小值为,
故,解得或(舍去);
当时,在上的最大值为,最小值为,
故,解得或(舍去),
综上或.
故答案为:或
6.(2023·全国·高三专题练习)不等式对任意都成立,则实数的取值范围 .
【答案】.
【分析】分离参数,换元法求最值,可得实数的取值范围.
【详解】原不等式可化为对恒成立,
令,则,所以,
当时,,所以.
故答案为: .
7.(2023秋·江西宜春·高三校考阶段练习)已知函数,若对, ,则实数的取值范围是 .
【答案】
【分析】由题设在对应区间上有,结合幂、指数函数性质求对应区间内、的最值,即可求参数范围.
【详解】由题意,在各对应区间上有,
而在的最小值为,在上的最小值为;
所以.
故答案为:
8.(2023·全国·高一课堂例题)讨论函数的单调性,并求最值.
【答案】在上单调递增,在上单调递减;最小值为2,无最大值
【分析】利用换元法,结合二次函数的性质以及复合函数单调性可直接求解.
【详解】,其中.
设,则,此时有,
当时,单调递增,由得.
又在上单调递增,
所以由复合函数的单调性的判定方法知,原函数在上单调递增.
同理,原函数在上单调递减.
故原函数有最小值,最小值为2,无最大值.
9.(2023春·四川达州·高一四川省万源中学校考阶段练习)已知函数且在上的最大值与最小值之差为.
(1)求实数a的值;
(2),若,求不等式的解集.
【答案】(1)或
(2)
【分析】(1)分和两种情况,结合指数函数单调性运算求解;
(2)根据题意可得:是奇函数且为增函数,利用函数的单调性和奇偶性解不等式.
【详解】(1)①当时,上单调递增,
则,
所以,解得或(舍去);
②当时,上单调递减
则,
所以,解得或(舍去);
综上所述:或.
(2)因为,由(1)可知:,则,
可知:的定义域为,
因为,则为奇函数,
又因为在上单调递增,则在上单调递增,
综上所述:在R上是奇函数且为增函数,
因为,可得,
则,解得或,
所以不等式的解集为.
【考点5:指数函数的应用】
【知识点:指数函数的应用】
1.(多选)(2023秋·山东枣庄·高一枣庄市第三中学校考期中)如图,在不对某种病毒采取任何防疫措施的情况下,从疫情发生开始某地区感染人数(千人)与时间(周)的关系式为(且),则下列说法中正确的有( )
A.疫情开始后,该地区每周新增加的感染人数都相等
B.随着时间推移,该地区后一周新增加的感染人数会是前一周的2倍
C.估计该地区感染人数翻一番所需时间只需1周
D.根据图象,估计疫情发生一个月后该地区感染人数会超过8000人
【答案】BCD
【分析】首先求函数的解析式,再结合选项,即可判断选项.
【详解】由图象可知,,即,得,
所以,
A.第三周,即时,感染人数为千人,
所以第一周到第二周增加1千人,第二周到第三周增加千人,故A错误;
B.由可知,第周的感染人数为,则第周的感染人数为,第周的感染人数为,
则第周新增感染人数为,第周新增感染人数为,,故B正确.
C.第一周是1千人,第二周是2千人,该地区感染人数翻一番所需时间只需1周,故C正确;
D.第四周,即时,感染人数千人,
所以估计疫情发生一个月后该地区感染人数会超过8000人,故D正确.
故选:BCD
2.(多选)(2023秋·广东惠州·高三校考阶段练习)某食品的保鲜时间(单位:小时)与储存温度(单位:℃)满足函数关系(,、为常数).若该食品在0℃的保鲜时间是120小时,在20℃的保鲜时间是30小时,则( )
A.
B.储存温度越高保鲜时间越长
C.在10℃的保鲜时间是60小时
D.在30℃的保鲜时间是15小时
【答案】ACD
【分析】由题意可知,,求得,进而可得,可判断A;利用单调性可判断B;计算可判断C;计算可判断D.
【详解】对于A,由题可知,,则,故,
所以,则,A正确;
对于B,由A可知,在上是减函数,且在上是增函数,
所以在上是减函数,则储存温度越高保鲜时间越短,B错误;
对于C,由A可知,小时,C正确;
对于D,由A可知,小时,D正确.
故选:ACD.
3.(2023·全国·高一课堂例题)某种放射性物质不断变化为其他物质,每经过1年,这种物质剩留的质量是原来的84%.写出这种物质的剩留量关于时间的函数关系式.
【答案】(,)
【分析】根据指数的运算性质即可求解.
【详解】设该物质最初的质量是1,经过x年剩留量是y.
经过1年,剩留量;
经过2年,剩留量;
……
一般地,经过x年,剩留量(,).函数
y=ax(a>0,且a≠1)
0
图象
图象
特征
在x轴上方,过定点(0,1)
当x逐渐增大时,
图象逐渐下降
当x逐渐增大时,
图象逐渐上升
…
0
1
2
…
…
0.25
0.5
1
2
4
…
…
0
0.5
1
…
…
0.1
0.32
1
3.16
10
…
函数
y=ax(a>0,且a≠1)
0
性
质
定义域
R
值域
(0,+∞)
函数
y=ax(a>0,且a≠1)
0
性质
单调性
在R上是减函数
在R上是增函数
函数值变
化规律
当x=0时,y=1
当x<0时,y>1;
当x>0时,0
高中第五章 三角函数5.3 诱导公式精品同步训练题: 这是一份高中<a href="/sx/tb_c4000282_t7/?tag_id=28" target="_blank">第五章 三角函数5.3 诱导公式精品同步训练题</a>,文件包含专题53诱导公式7类必考点人教A版2019必修第一册原卷版docx、专题53诱导公式7类必考点人教A版2019必修第一册解析版docx等2份试卷配套教学资源,其中试卷共24页, 欢迎下载使用。
高中数学人教A版 (2019)必修 第一册4.4 对数函数优秀一课一练: 这是一份高中数学人教A版 (2019)必修 第一册<a href="/sx/tb_c4000276_t7/?tag_id=28" target="_blank">4.4 对数函数优秀一课一练</a>,文件包含专题44对数函数5类必考点人教A版2019必修第一册原卷版docx、专题44对数函数5类必考点人教A版2019必修第一册解析版docx等2份试卷配套教学资源,其中试卷共33页, 欢迎下载使用。
人教A版 (2019)必修 第一册4.3 对数优秀随堂练习题: 这是一份人教A版 (2019)必修 第一册<a href="/sx/tb_c4000275_t7/?tag_id=28" target="_blank">4.3 对数优秀随堂练习题</a>,文件包含专题43对数4类必考点人教A版2019必修第一册原卷版docx、专题43对数4类必考点人教A版2019必修第一册解析版docx等2份试卷配套教学资源,其中试卷共16页, 欢迎下载使用。













