人教版八年级上册13.3.1 等腰三角形教学演示课件ppt

这是一份人教版八年级上册13.3.1 等腰三角形教学演示课件ppt，共26页。PPT课件主要包含了知识点1，等腰三角形的判定，方法一，方法二，知识点2，等腰三角形判定的应用，BECD，解是等腰三角形等内容，欢迎下载使用。

掌握等腰三角形的判定方法。(重点) 掌握等腰三角形的判定定理，并运用其进行证明和计算。(难点)
1.等腰三角形的性质有哪些？
等腰三角形的两个底角相等(简写成“等边对等角”)；
等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合(简写成“三线合一”)．
2.应用这些性质的前提是什么？
前提是这个三角形的等腰三角形.
3.如何判定一个三角形是等腰三角形？
定义：有两条边相等的三角形是等腰三角形.
如图，位于海上 B,C两处的两艘救生船接到A 处遇险船只的报警，当时测得∠B=∠C.如果这两艘救生船以同样的速度同时出发，能不能同时赶到出事地点 (不考虑风浪因素) ？
猜想：若∠B=∠C，则AB=AC
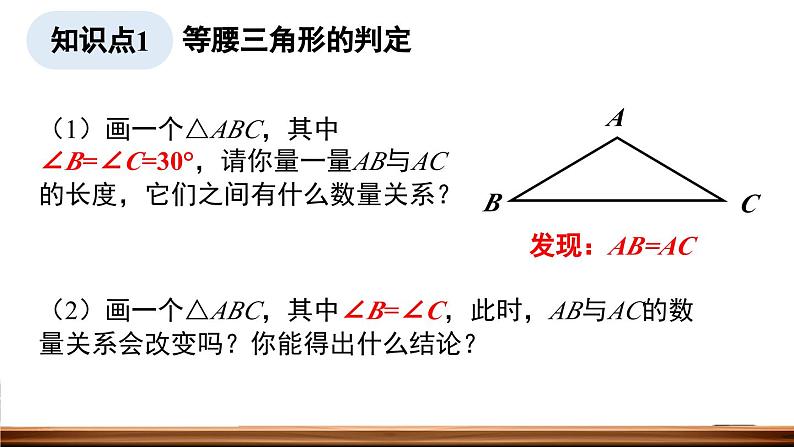
（1）画一个△ABC，其中∠B=∠C=30°，请你量一量AB与AC的长度，它们之间有什么数量关系？
（2）画一个△ABC，其中∠B=∠C，此时，AB与AC的数量关系会改变吗？你能得出什么结论？
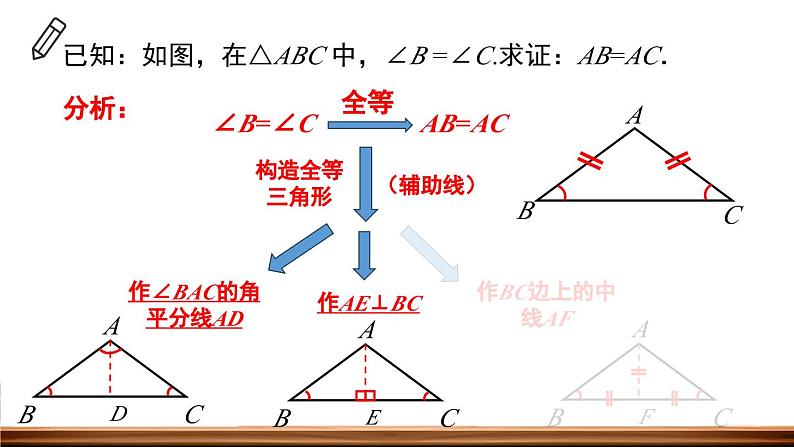
已知：如图，在△ABC 中，∠B =∠C.求证：AB=AC．
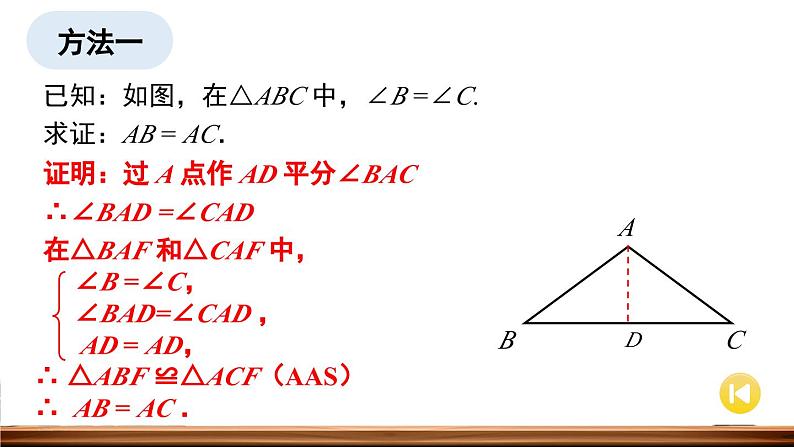
证明：过 A 点作 AD 平分∠BAC ∴∠BAD =∠CAD在△BAF 和△CAF 中，
∴ △ABF ≌△ACF（AAS） ∴ AB = AC ．
已知：如图，在△ABC 中，∠B =∠C.求证：AB = AC．
证明：过 A 点作 AF⊥BC，垂足为 F.在△BAF 和△CAF 中，
　　等腰三角形的判定方法：
符号语言：在△ABC 中，∵∠B =∠C（已知），∴AB =AC（等角对等边）．即△ABC为等腰三角形
如果一个三角形有两个角相等，那么这两个角所对的边也相等（简写成“等角对等边”）.
与等腰三角形性质进行比较,两者有什么区别？
比较等腰三角形的性质和等腰三角形的判定
1.已知△ABC的三边长分别是a，b，c，则下列条件中，不能判定△ABC是等腰三角形的是（ ）
A. a∶b ∶ c=2∶3∶4B. a=3，b=4，c=3C.∠B=50°，∠C＝80°D.∠A∶∠B∶∠C=1∶1∶2
2.如图，在△ABC中，∠A=36°，AB=AC，BD平分∠ABC，则图中等腰三角形的个数是（ ）
A.0 B.1C.2 D.3
求证：如果三角形一个外角的平分线平行于三角形的一边，那么这个三角形是等腰三角形.
已知：∠CAE 是△ABC 的外角，∠1 =∠2，AD∥BC．求证：AB =AC.
证明：∵　AD∥BC ，∴　∠1 =（ 　　 ）， ∠2 =∠C（ 　 　）．
两直线平行，同位角相等
两直线平行，内错角相等
∵　∠1 =∠2，∴　∠B =∠C．∴　AB =AC
已知等腰三角形底边长为a ，底边上的高的长为h ，求作这个等腰三角形.
(1) 作线段 AB =a；(2) 作线段 AB 的垂直平分线 MN，与 AB 相交于点 D；(3) 在 MN上取一点 C，使 DC =h； (4) 连接 AC，BC，则△ABC 就是所求作的等腰三角形.
1. 如图所示，已知 OC 平分∠AOB，CD∥OB. 若 OD = 3，则 CD 等于（ ）
A.3cm D.2cm
2. 如图所示，在△ABC中，已知AB=AC，要使AD = AE，需要添加的一个条件是 __________. （答案不唯一）
【课本P79 练习 第1题】
3. 如图，∠A=36°，∠ DBC=36°， ∠C=72°.分别计算∠1，∠2的度数，并说明图中有哪些等腰三角形.
解：∵∠ DBC=36°， ∠C=72°，∴∠1=180°－∠DBC－∠C=180°－36°－72°=72°.又∠1是△ABD的一个外角，∴∠1=∠A＋∠2.∴∠2=∠1－∠A=72°－36°＝36°又∠2=∠A=36°，∠1=∠C=72°，∴∠ABC=∠C=72°∴AD=BD，BC=BD，AB=AC.图中共有三个等腰三角形，即△ABD，△BDC，△ABC.
4.如图，把一张长方形的纸沿着对角线折叠，重合部分是一个等腰三角形吗？为什么？
∵ △ABD≌ △CDB，∴∠ADB=∠CBD，∴ △EBD是等腰三角形.
【课本P79 练习 第2题】
【课本P79 练习 第3题】
5.求证：如果三角形一条边上的中线等于这条边的一半，那么这个三角形是直角三角形.
6.如图，AC 和 BD 相交于 O点，且 AB∥DC，OA =OB. 求证 OC= OD.
证明：∵OA=OB， ∴∠A=∠B， 又∵AB∥DC， ∴∠C=∠A=∠D=∠B， ∴OC=OD.
【课本P79 练习 第4题】
7. 已知：CE、CF分别平分∠ACB和它的外角∠ACM，EF∥BC，EF交AC于点D，E是CE与AB的交点. 求证：DE=DF.
证明：∵CF平分∠ACM， CE平分∠ACB， ∴∠ACF=∠MCF.∴∠ACE=∠BCE.∵EF∥BC，∴∠F=∠MCF=∠ACF，∠FEC=∠BCE=∠ACE，∴DF=DC，DE=DC，∴DE=DF.
8.（1）如图，在△ABC中，AB=AC，∠ABC、∠ACB的平分线相交于点F，过F作DE∥BC，交AB于点D，交AC于E．问图中哪些三角形是等腰三角形？（2）上题中，若去掉条件AB=AC，其他条件不变，图中还有等腰三角形吗？
（2）△BDF和△CEF是等腰三角形.∵BF平分∠ABC，CF平分∠ACB，∴∠ABF=∠CBF，∠ACF=∠BCF.又DE∥BC，∴∠DFB=∠CBF=∠ABF，∠EFC=∠BCF=∠ACF，∴DF=DB，EF=EC.∴△BDF和△CEF是等腰三角形.
解：（1）△ABC，△ADE，△BDF，△CEF，△BCF 都是等腰三角形.