2024年中考数学二轮复习 二次函数压轴题 专项提升练习四（含答案）

这是一份2024年中考数学二轮复习 二次函数压轴题 专项提升练习四（含答案），共14页。试卷主要包含了﹣2eq \r)代入，得，2．等内容，欢迎下载使用。
定义：若一个函数的图象上存在横、纵坐标之和为零的点，则称该点为这个函数图象的“好点”．例如，点(﹣1，1)是函数y＝x＋2的图象的“好点”．
(1)在函数①y＝﹣x＋3，②y＝③y＝x2＋2x＋1的图象上，存在“好点”的函数是 ；(填序号)
(2)设函数y＝﹣eq \f(4,x)(x＜0)与y＝kx＋3的图象的“好点”分别为点A、B，过点A作AC⊥y轴，垂足为C．当△ABC为等腰三角形时，求k的值；
(3)若将函数y＝x2＋2x的图象在直线y＝m下方的部分沿直线y＝m翻折，翻折后的部分与图象的其余部分组成了一个新的图象．当该图象上恰有3个“好点”时，求m的值．
如图，点A在x轴上，OA＝4，将线段OA绕点O顺时针旋转120°至OB的位置.
(1)求点B的坐标；
(2)求经过点A、O、B的抛物线的解析式；
(3)在此抛物线的对称轴上，是否存在点P，使得以点P、O、B为顶点的三角形是等腰三角形？若存在，求点P的坐标；若不存在，说明理由.
如图，在平面直角坐标系xOy中，直线y＝﹣eq \f(4,3)x＋4与x轴、y轴分别交于A、C两点，抛物线y＝﹣eq \f(1,3)x2＋bx＋c经过A、C两点．
(1)求抛物线的解析式；
(2)点B为y轴上一点，点P为直线AB上一点，过P作PQ∥BC交x轴于点Q，当四边形BCPQ为菱形时，请直接写出B点坐标；
(3)在(2)的条件下，且点B在线段OC上时，将抛物线y＝﹣eq \f(1,3)x2＋bx＋c向上平移m个单位，平移后的抛物线与直线AB交于点D(点D在第二象限)，点N为x轴上一点，若∠DNB＝90°，且符合条件的点N恰好有2个，求m的取值范围．
如图，在平面直角坐标系中，抛物线y=ax2+bx+c与x轴交于点A(﹣2，0)，点B(4，0)，与y轴交于点C(0，8)，连接BC，又已知位于y轴右侧且垂直于x轴的动直线l，沿x轴正方向从O运动到B(不含O点和B点)，且分别交抛物线、线段BC以及x轴于点P，D，E．
(1)求抛物线的表达式；
(2)连接AC，AP，当直线l运动时，求使得△PEA和△AOC相似的点P的坐标；
(3)作PF⊥BC，垂足为F，当直线l运动时，求Rt△PFD面积的最大值．
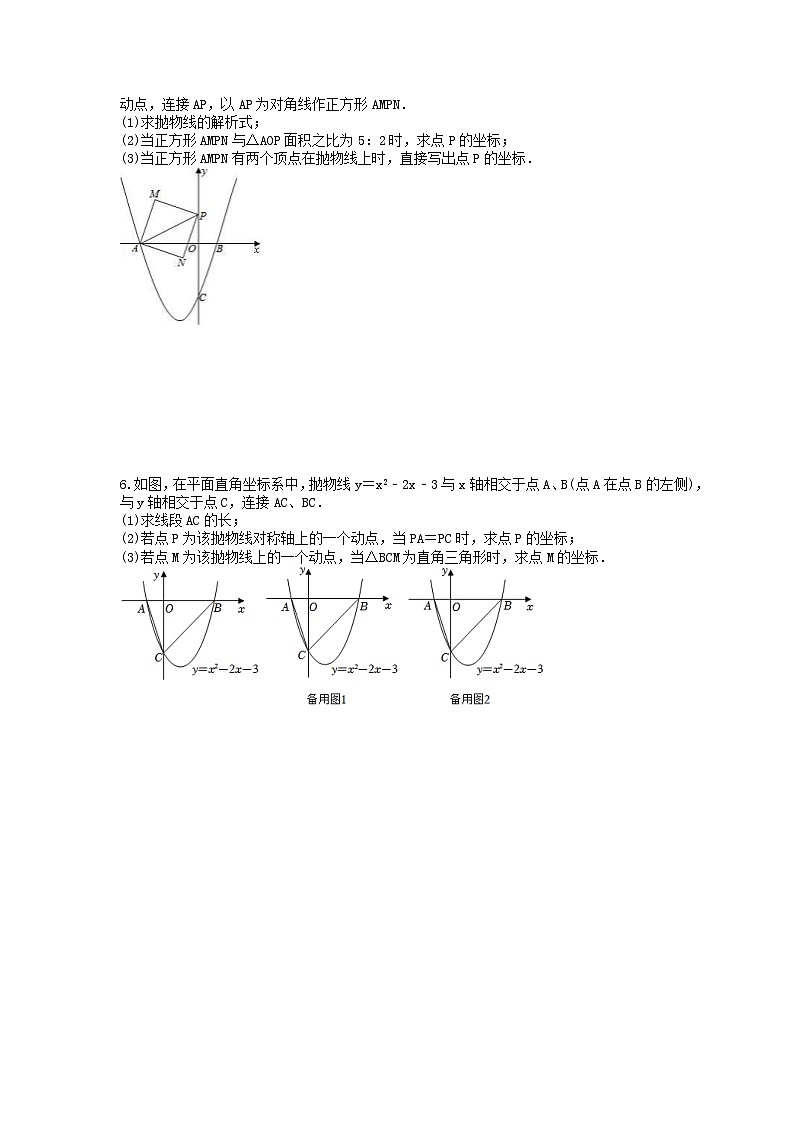
如图，抛物线y＝x2＋bx＋c经过A(﹣3，0)，B(1，0)两点，与y轴交于点C，P为y轴上的动点，连接AP，以AP为对角线作正方形AMPN．
(1)求抛物线的解析式；
(2)当正方形AMPN与△AOP面积之比为5：2时，求点P的坐标；
(3)当正方形AMPN有两个顶点在抛物线上时，直接写出点P的坐标．
如图，在平面直角坐标系中，抛物线y＝x2﹣2x﹣3与x轴相交于点A、B(点A在点B的左侧)，与y轴相交于点C，连接AC、BC．
(1)求线段AC的长；
(2)若点P为该抛物线对称轴上的一个动点，当PA＝PC时，求点P的坐标；
(3)若点M为该抛物线上的一个动点，当△BCM为直角三角形时，求点M的坐标．
如图1，已知抛物线L：y＝ax2＋bx﹣eq \f(3,2)(a＞0)与x轴交于点A(-1,0)和点B，顶点为M，对称轴为直线l：x＝1.
(1)直接写出点B的坐标及一元二次方程ax2＋bx﹣eq \f(3,2)＝0的解.
(2)求抛物线L的解析式及顶点M的坐标.
(3)如图2，设点P是抛物线L上的一个动点，将抛物线L平移.使它的頂点移至点P，得到新抛物线L′，L′与直线l相交于点N.设点P的横坐标为m
①当m＝5时，PM与PN有怎样的数量关系？请说明理由.
②当m为大于1的任意实数时，①中的关系式还成立吗？为什么？
③是否存在这样的点P，使△PMN为等边三角形？若存在.请求出点P的坐标；若不存在，请说明理由.
如图，在平面直角坐标系中，已知抛物线y=ax2＋bx﹣2(a≠0)与x轴交于A(1，0)、B(3，0)两点，与y轴交于点C，其顶点为点D，点E的坐标为(0，﹣1)，该抛物线与BE交于另一点F，连接BC．
(1)求该抛物线的解析式，并用配方法把解析式化为y=a(x﹣h)2＋k的形式；
(2)若点H(1，y)在BC上，连接FH，求△FHB的面积；
(3)一动点M从点D出发，以每秒1个单位的速度平沿行与y轴方向向上运动，连接OM，BM，设运动时间为t秒(t＞0)，在点M的运动过程中，当t为何值时，∠OMB=90°？
(4)在x轴上方的抛物线上，是否存在点P，使得∠PBF被BA平分？若存在，请直接写出点P的坐标；若不存在，请说明理由．
\s 0 答案
解：(1)∵y＝﹣x＋3，
∴y＋x＝3，
∴①不是“好点”的函数，
∵y＝，x＞0，
∴xy＝3＞0
∴x＋y≠0，
∴②不是“好点”的函数，
∵，
∴x2＋3x＋1＝0，
∴Δ＝32﹣4×1×1＞0，
∴方程组有解，
∴③是“好点”的函数，故答案为：③；
(2)∵，x＜0，∴，∴A(﹣2，2)，如图，
当△ABC为等腰三角形时，AB＝AC＝2或BA＝BC，当AB＝AC时，
∵y＝﹣x，
∴B(x，﹣x)，
∴(x＋2)2＋(﹣x﹣2)2＝22，
∴x1＝eq \r(2)﹣2，x2＝﹣eq \r(2)﹣2，
当x＝eq \r(2)﹣2时，y＝﹣eq \r(2)＋2，
∴(eq \r(2)﹣2)k＋3＝﹣eq \r(2)＋2，
∴k＝eq \f(3\r(2),2)﹣2，
当x＝﹣eq \r(2)﹣2时，y＝eq \r(2)＋2，
∴(﹣eq \r(2)﹣2)k＋3＝eq \r(2)＋2，
∴k＝﹣eq \f(3\r(2),2)﹣2，
当AB＝BC时，点B(﹣1，1)，
∴﹣k＋3＝1，
∴k＝2，
综上所述：k＝±(eq \f(3\r(2),2)﹣2)或k＝2；
(3)设翻折后的抛物线解析式为y＝﹣x2﹣2x＋k，
∵y＝x2＋2x的图像上有两个“好点”：(0，0)和(﹣3，0)，
当y＝﹣x2﹣2x＋k上有一个“好点”时，
把y＝﹣x代入得，﹣x＝﹣x2﹣2x＋k，
化简整理得，x2＋x﹣k＝0，
∵Δ＝1＋4k＝0，
∴k＝﹣eq \f(1,4)，∴y＝﹣x2﹣2x﹣eq \f(1,4)，
由得，
2y＝﹣eq \f(1,4)，∴y＝﹣eq \f(1,8)，∴m＝﹣eq \f(1,8)．
当(0，0)在y＝﹣x2﹣2x＋k上时，此时﹣x2﹣2x＝﹣x，x＝0或x＝﹣1，
这时也有三个“好点”：(﹣3，﹣3)，(0，0)，(﹣1﹣1)，
∴m＝﹣eq \f(1,8)或0．
解：(1)如图，过B点作BC⊥x轴，垂足为C，则∠BCO＝90°，
∵∠AOB＝120°，
∴∠BOC＝60°，
又∵OA＝OB＝4，
∴OC＝eq \f(1,2)OB＝eq \f(1,2)×4＝2，BC＝OB•sin60°＝4×eq \f(\r(3),2)＝2eq \r(3)，
∴点B的坐标为(﹣2，﹣2eq \r(3))；
(2)∵抛物线过原点O和点A、B，
∴可设抛物线解析式为y＝ax2＋bx，
将A(4，0)，B(﹣2.﹣2eq \r(3))代入，得：
，解得，
∴此抛物线的解析式为y＝﹣eq \f(\r(3),6)x2＋eq \f(2\r(3),3)x；
(3)存在；如图，抛物线的对称轴是直线x＝2，直线x＝2与x轴的交点为D，设点P的坐标为(2，y)，
①若OB＝OP，则22＋|y|2＝42，解得y＝±2eq \r(3)，
当y＝2eq \r(3)时，在Rt△P′OD中，∠P′DO＝90°，sin∠P′OD＝eq \f(\r(3),2)，
∴∠P′OD＝60°，
∴∠P′OB＝∠P′OD＋∠AOB＝60°＋120°＝180°，
即P′、O、B三点在同一直线上，
∴y＝2eq \r(3)不符合题意，舍去，
∴点P的坐标为(2，﹣2eq \r(3))
②若OB＝PB，则42＋|y＋2eq \r(3)|2＝42，解得y＝﹣2eq \r(3)，
故点P的坐标为(2，﹣2eq \r(3))，
③若OP＝BP，则22＋|y|2＝42＋|y＋2eq \r(3)|2，解得y＝﹣2eq \r(3)，
故点P的坐标为(2，﹣2eq \r(3))，
综上所述，符合条件的点P只有一个，其坐标为(2，﹣2eq \r(3)).
方法二：
(3)设P(2，t)，O(0，0)，B(﹣2，﹣2eq \r(3))，
∵△POB为等腰三角形，
∴PO＝PB，PO＝OB，PB＝OB，
(2﹣0)2＋(t﹣0)2＝(2＋2)2＋(t＋2eq \r(3))2，∴t＝﹣2eq \r(3)，
(2﹣0)2＋(t﹣0)2＝(0＋2)2＋(0＋2eq \r(3))2，∴t＝2eq \r(3)或﹣2eq \r(3)，
当t＝2eq \r(3)时，P(2，2eq \r(3))，O(0，0)B(﹣2，﹣2eq \r(3))三点共线故舍去，
(2＋2)2＋(t＋2eq \r(3))2＝(0＋2)2＋(0＋2eq \r(3))2，∴t＝﹣2eq \r(3)，
∴符合条件的点P只有一个，∴P(2，﹣2eq \r(3)).
方法二追加第(4)问：在(3)的条件下，⊙M为△OBP的外接圆，求出圆心M的坐标.
(4)∵点B，点P关于y轴对称，
∴点M在y轴上，设M(0，m)，
∵⊙M为△OBF的外接圆，
∴MO＝MB，
∴(0﹣0)2＋(m﹣0)2＝(0＋2)2＋(m＋2eq \r(3))2，
∴m＝﹣eq \f(4\r(3),3)，M(0，﹣eq \f(4\r(3),3)).
解：(1)由题意得，
A(3，0)，C(0，4)，
∴，∴，
∴抛物线解析式为；
(2)如图1，
设B(0，a)，
∴PQ＝BC＝BQ＝4﹣a，
∵A(3，0)，
∴直线AB的解析式是：y＝﹣，
由﹣＝4﹣a得，x＝，
∴OQ＝，
∵四边形BCPQ是菱形，
∴PB⊥CQ，
∵∠ABO＝∠PBC，
∴∠OCQ＝∠BAO，
∴△AOB∽△COQ，
∴＝，
∴＝，
∴a1＝eq \f(3,2)，a2＝﹣6，
∴B1(0,eq \f(3,2))，B2(0，﹣6)；
(3)如图2，
由(2)知，B(0，eq \f(3,2))，
∴直线AB的解析式是：y＝﹣eq \f(1,2)x+eq \f(3,2)，
∴设D(a，﹣﹣eq \f(1,2)a+eq \f(3,2))，
∴BD2＝(a2＋eq \f(1,4)a2)＝eq \f(5,4)a2，
∵∠DNB＝90°，且符合条件的点N恰好有2个，
以BD为直径的圆与x轴相交，设圆心为I，则I(，﹣)，
作IJ⊥OA于J，∴IJ＜BD，∴(﹣)2＜，
∴a1＜，a2＞ (舍去)，
当a＝时，y＝﹣×＝，
设平移后的抛物线为：
将D点坐标代入平移后解析式得，
﹣×()2＋4＋m＝解得：m＝，
∴m＞．
解：(1)将点A、B、C的坐标代入二次函数表达式得：
，解得：，
故抛物线的表达式为：y=﹣x2+2x+8；
(2)∵点A(﹣2，0)、C(0，8)，∴OA=2，OC=8，
∵l⊥x轴，∴∠PEA=∠AOC=90°，
∵∠PAE≠∠CAO，
∴只有当∠PEA=∠AOC时，PEA△∽AOC，
此时，即：，∴AE=4PE，
设点P的纵坐标为k，则PE=k，AE=4k，∴OE=4k﹣2，
将点P坐标(4k﹣2，k)代入二次函数表达式并解得：
k=0或 (舍去0)，则点P(，)；
(3)在Rt△PFD中，∠PFD=∠COB=90°，
∵l∥y轴，∴∠PDF=∠COB，∴Rt△PFD∽Rt△BOC，
∴，∴S△PDF=×S△BOC，
而S△BOC=eq \f(1,2)OB×OC16，BC==4，
∴S△PDF=×S△BOC=eq \f(1,5)PD2，即当PD取得最大值时，S△PDF最大，
将B、C坐标代入一次函数表达式并解得：直线BC的表达式为：y=﹣2x+8，
设点P(m，﹣m2+2m+8)，则点D(m，﹣2m+8)，
则PD=﹣m2+2m+8+2m﹣8=﹣(m﹣2)2+4，
当m=2时，PD的最大值为4，
故当PD=4时，∴S△PDF=eq \f(1,5)PD2=3.2．
解：(1)把A(﹣3，0)，B(1，0)代入y＝x2＋bx＋c得，
，解得，
∴抛物线的关系式为y＝x2＋2x﹣3．
(2)设P的纵坐标为y．∵正方形AMPN与△AOP面积之比为5：2．
∴eq \f(1,2)(32＋y2)＝eq \f(5,2)×eq \f(1,2)×3×|y|．解得：y＝±eq \f(3,2)或＝±6．
∴点P的坐标为：P1(0，eq \f(3,2))或P2(0，﹣eq \f(3,2))或P3(0，6)或P4(0，﹣6)．
(3)设P(0，m)，连接MN交AP于T，过点T作TJ⊥OA于J，过点P作PE⊥TJ于E，过点N作NF⊥TJ于F，过点M作MG⊥TJ于G．
∵四边形AMPN是正方形，
∴TA＝TP＝TM＝TN，AP⊥MN，
∵A(﹣3，0)，P(0，m)，
∴T(﹣eq \f(3,2)，eq \f(1,2)m)，
∵∠PET＝∠F＝∠PTN＝90°，
∴∠PTE＋∠NTF＝90°，∠NTF＋∠TNF＝90°，
∴∠PTE＝∠TNF，
∴△PET≌△TFN(AAS)，
∴ET＝FN，PE＝TF，
同法可证△PET≌△TGM，
∴MG＝ET＝FN，GT＝PE＝TF，
∴M(﹣eq \f(3,2)﹣eq \f(1,2)m，eq \f(1,2)m＋eq \f(3,2))，N(﹣eq \f(3,2)＋eq \f(1,2)m，eq \f(1,2)m﹣eq \f(3,2))，
当点M在抛物线上时，eq \f(1,2)m＋eq \f(3,2)＝(﹣eq \f(3,2)﹣eq \f(1,2)m)2＋2(﹣eq \f(3,2)﹣eq \f(1,2)m)﹣3，解得m＝±eq \r(21)，
当点N在抛物线上时，eq \f(1,2)m﹣eq \f(3,2)＝(﹣eq \f(3,2)＋eq \f(1,2)m)2＋2(﹣eq \f(3,2)＋eq \f(1,2)m)﹣3，解得m＝2±eq \r(13)
∴满足条件的点P的坐标是：(0，eq \r(21))或(0，﹣eq \r(21))或(0，2﹣eq \r(13))或(0，2＋eq \r(13))．
解：(1)针对于抛物线y＝x2﹣2x﹣3，令x＝0，则y＝﹣3，
∴C(0，﹣3)；
令y＝0，则x2﹣2x﹣3＝0，
∴x＝3或x＝﹣1，
∵点A在点B的左侧，
∴A(﹣1，0)，B(3，0)，
∴AC＝eq \r(10)；
(2)∵抛物线y＝x2﹣2x﹣3的对称轴为直线x＝1，
∵点P为该抛物线对称轴上，
∴设P(1，p)，
∴PA＝，PC＝，
∵PA＝PC，
∴＝，
∴p＝﹣1，
∴P(1，﹣1)；
(3)由(1)知，B(3，0)，C(0，﹣3)，
∴OB＝OC＝3，
设M(m，m2﹣2m﹣3)，
∵△BCM为直角三角形，
∴①当∠BCM＝90°时，
如图1，过点M作MH⊥y轴于H，则HM＝m，
∵OB＝OC，
∴∠OCB＝∠OBC＝45°，
∴∠HCM＝90°﹣∠OCB＝45°，
∴∠HMC＝45°＝∠HCM，
∴CH＝MH，
∵CH＝﹣3﹣(m2﹣2m﹣3)＝﹣m2＋2m，
∴﹣m2＋2m＝m，
∴m＝0(不符合题意，舍去)或m＝1，
∴M(1，﹣4)；
②当∠CBM＝90°时，
过点M作M'H'⊥x轴，
同①的方法得，M'(﹣2，5)；
③当∠BMC＝90°时，如图2，
Ⅰ、当点M在第四象限时，
过点M作MD⊥y轴于D，过点B作BE⊥DM，交DM的延长线于E，

∴∠CDM＝∠E＝90°，
∴∠DCM＋∠DMC＝90°，
∵∠DMC＋∠EMB＝90°，
∴∠DCM＝∠EMB，
∴△CDM∽△MEB，
∴，
∵M(m，m2﹣2m﹣3)，B(3，0)，C(0，﹣3)，
∴DM＝m，CD＝﹣3﹣(m2﹣2m﹣3)＝﹣m2＋2m，ME＝3﹣m，
BE＝﹣(m2﹣2m﹣3)＝﹣m2＋2m＋3，
∴，
∴m＝0(舍去)或m＝3(点B的横坐标，不符合题意，舍去)
或m＝eq \f(1－\r(5),2)(不符合题意，舍去)或m＝eq \f(1＋\r(5),2)，
∴M(，﹣)，
Ⅱ、当点M在第三象限时，M(，﹣)，
即满足条件的M的坐标为(1，﹣4)或(﹣2，5)
或(，﹣)，或(，﹣)．
解：(1)如图1，∵y＝ax2＋bx﹣eq \f(3,2)(a＞0)与x轴交于点A(﹣1，0)和点B，
对称轴为直线l：x＝1，
∴点A和点B关于直线l：x＝1对称，
∴点B(3，0)，
∴一元二次方程ax2＋bx﹣eq \f(3,2)＝0的解为x1＝﹣1，x2＝3；
(2)把A(﹣1，0)，B(3，0)代入y＝ax2＋bx﹣eq \f(3,2)，
得，解得，
抛物线L的解析式为y＝eq \f(1,2)x2﹣x﹣eq \f(3,2)，
配方得，y＝eq \f(1,2)(x﹣1)2﹣2，所以顶点M的坐标为(1，﹣2)；
(3)如图2，作PC⊥l于点C.
①∵y＝eq \f(1,2)(x﹣1)2﹣2，
∴当m＝5，即x＝5时，y＝6，
∴P(5，6)，
∴此时L′的解析式为y＝eq \f(1,2)(x﹣5)2＋6，点C的坐标是(1，6).
∵当x＝1时，y＝14，
∴点N的坐标是(1，14).
∵CM＝6﹣(﹣2)＝8，CN＝14﹣6＝8，
∴CM＝CN.
∵PC垂直平分线段MN，
∴PM＝PN；
②PM＝PN仍然成立.由题意有点P的坐标为(m，eq \f(1,2)m2﹣m﹣eq \f(3,2)).
∵L′的解析式为y＝eq \f(1,2)(x﹣m)2＋eq \f(1,2)m2﹣m﹣1.5，
∴点C的坐标是(1，eq \f(1,2)m2﹣m﹣eq \f(3,2))，
∴CM＝eq \f(1,2)m2﹣m﹣1.5＋2＝eq \f(1,2)m2﹣m＋eq \f(1,2).
∵在L′的解析式y＝eq \f(1,2)(x﹣m)2＋eq \f(1,2)m2﹣m﹣eq \f(3,2)中，
∴当x＝1时，y＝m2﹣2m﹣1，
∴点N的坐标是(1，m2﹣2m﹣1)，
∴CN＝(m2﹣2m﹣1)﹣(eq \f(1,2)m2﹣m﹣1.5)＝eq \f(1,2)m2﹣m＋eq \f(1,2)，
∴CM＝CN.
∵PC垂直平分线段MN，
∴PM＝PN；
③存在这样的点P，使△PMN为等边三角形.若CN:PC＝tan30°，则eq \f(1,2)m2﹣m＋eq \f(1,2)＝eq \f(\r(3),3)(m﹣1)，
解得m＝eq \f(2\r(3),3)＋1，所以点P的坐标为(eq \f(2\r(3),3)＋1，﹣eq \f(4,3)).
解：(1)∵抛物线y=ax2＋bx﹣2(a≠0)与x轴交于A(1，0)、B(3，0)两点，
∴∴，
∴抛物线解析式为y=﹣eq \f(2,3)x2＋eq \f(8,3)x﹣2=﹣eq \f(2,3)(x﹣2)2＋eq \f(4,3)；
(2)如图1，
过点A作AH∥y轴交BC于H，BE于G，由(1)有，C(0，﹣2)，
∵B(0，3)，∴直线BC解析式为y=eq \f(2,3)x﹣2，
∵H(1，y)在直线BC上，∴y=﹣eq \f(4,3)，∴H(1，﹣eq \f(4,3))，
∵B(3，0)，E(0，﹣1)，∴直线BE解析式为y=﹣eq \f(1,3)x﹣1，∴G(1，﹣eq \f(2,3))，∴GH=eq \f(2,3)，
∵直线BE：y=﹣eq \f(1,3)x﹣1与抛物线y=﹣eq \f(2,3)x2＋eq \f(8,3)x﹣2相较于F，B，∴F(eq \f(1,2)，﹣eq \f(5,6))，
∴S△FHB=eq \f(1,2)GH×|xG﹣xF|＋eq \f(1,2)GH×|xB﹣xG|=eq \f(1,2)GH×|xB﹣xF|=eq \f(1,2)×eq \f(2,3)×(3﹣eq \f(1,2))=eq \f(5,6)．
(3)如图2，由(1)有y=﹣eq \f(2,3)x2＋eq \f(8,3)x﹣2，∵D为抛物线的顶点，∴D(2，eq \f(4,3))，
∵一动点M从点D出发，以每秒1个单位的速度平沿行与y轴方向向上运动，
∴设M(2，m)，(m＞eq \f(4,3))，∴OM2=m2＋4，BM2=m2＋1，AB2=9，
∵∠OMB=90°，∴OM2＋BM2=AB2，∴m2＋4＋m2＋1=9，
∴m=eq \r(2)或m=﹣eq \r(2)(舍)，∴M(0，eq \r(2))，∴MD=eq \r(2)﹣eq \f(4,3)，
∵一动点M从点D出发，以每秒1个单位的速度平沿行与y轴方向向上运动，∴t=eq \r(2)﹣eq \f(4,3)；
(4)存在点P，使∠PBF被BA平分，∴∠PBO=∠EBO，∵E(0，﹣1)，
∴在y轴上取一点N(0，1)，∵B(3，0)，∴直线BN的解析式为y=﹣eq \f(1,3)x＋1①，
∵点P在抛物线y=﹣eq \f(2,3)x2＋eq \f(8,3)x﹣2②上，联立①②得，
或(舍)，∴P(eq \f(3,2)，eq \f(1,2))，
即：在x轴上方的抛物线上，存在点P，使得∠PBF被BA平分，P(eq \f(3,2)，eq \f(1,2))．