2024年中考数学二轮复习 二次函数压轴题 专项提升练习五（含答案）

这是一份2024年中考数学二轮复习 二次函数压轴题 专项提升练习五（含答案），共14页。
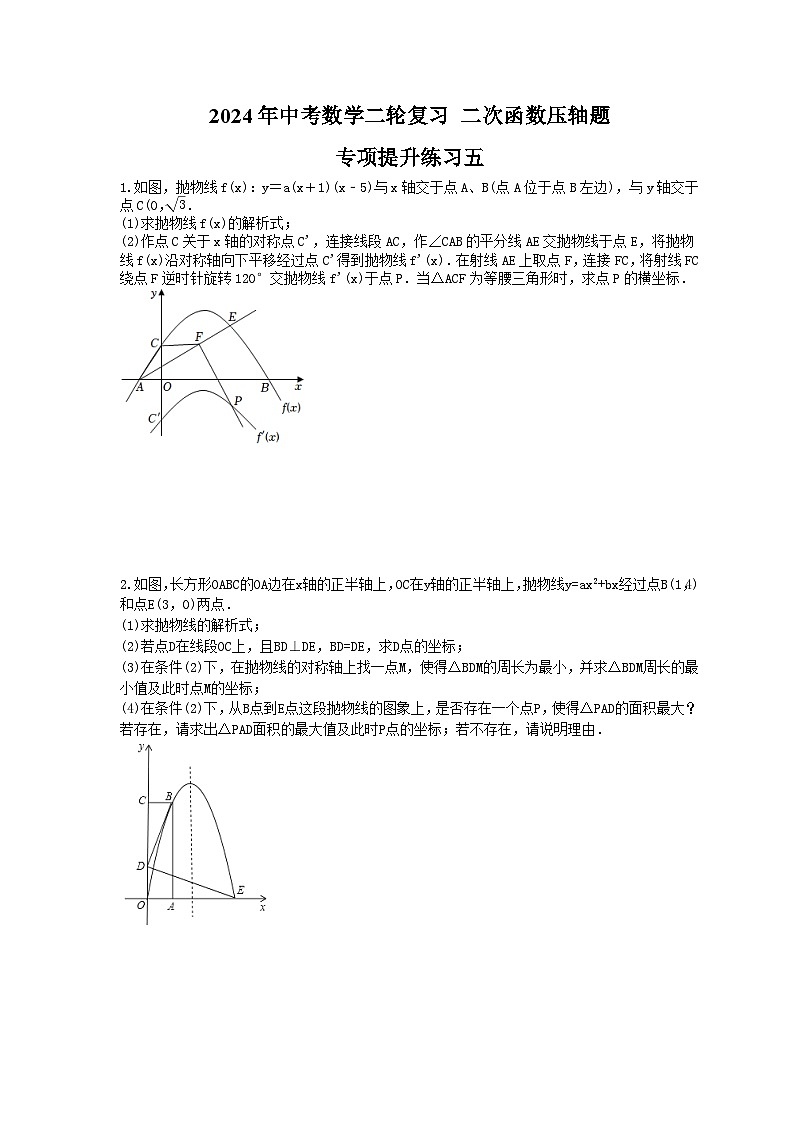
如图，抛物线f(x)：y＝a(x＋1)(x﹣5)与x轴交于点A、B(点A位于点B左边)，与y轴交于点C(0，eq \r(3)．
(1)求抛物线f(x)的解析式；
(2)作点C关于x轴的对称点C'，连接线段AC，作∠CAB的平分线AE交抛物线于点E，将抛物线f(x)沿对称轴向下平移经过点C'得到抛物线f'(x)．在射线AE上取点F，连接FC，将射线FC绕点F逆时针旋转120°交抛物线f'(x)于点P．当△ACF为等腰三角形时，求点P的横坐标．
如图，长方形OABC的OA边在x轴的正半轴上，OC在y轴的正半轴上，抛物线y=ax2+bx经过点B(1，4)和点E(3，0)两点．
(1)求抛物线的解析式；
(2)若点D在线段OC上，且BD⊥DE，BD=DE，求D点的坐标；
(3)在条件(2)下，在抛物线的对称轴上找一点M，使得△BDM的周长为最小，并求△BDM周长的最小值及此时点M的坐标；
(4)在条件(2)下，从B点到E点这段抛物线的图象上，是否存在一个点P，使得△PAD的面积最大？若存在，请求出△PAD面积的最大值及此时P点的坐标；若不存在，请说明理由．
已知抛物线y＝ax2﹣mx＋2m﹣3经过点A(2，﹣4)．
(1)求a的值；
(2)若抛物线与y轴的公共点为(0，﹣1)，抛物线与x轴是否有公共点，若有，求出公共点的坐标；若没有，请说明理由；
(3)当2≤x≤4时，设二次函数y＝ax2﹣mx＋2m﹣3的最大值为M，最小值为N，若＝，求m的值．
如图，已知抛物线经过原点O，顶点为A(1，1)，且与直线y=x﹣2交于B，C两点．
(1)求抛物线的解析式及点C的坐标；
(2)求证：△ABC是直角三角形；
(3)若点N为x轴上的一个动点，过点N作MN⊥x轴与抛物线交于点M，则是否存在以O，M，N为顶点的三角形与△ABC相似？若存在，请求出点N的坐标；若不存在，请说明理由．
如图，顶点为C的抛物线y＝ax2＋bx(a＞0)经过点A和x轴正半轴上的点B，连接OC、OA、AB，已知OA＝OB＝2，∠AOB＝120°.
(1)求这条抛物线的表达式；
(2)过点C作CE⊥OB，垂足为E，点P为y轴上的动点，若以O、C、P为顶点的三角形与△AOE相似，求点P的坐标；
(3)若将(2)的线段OE绕点O逆时针旋转得到OE′，旋转角为α(0°＜α＜120°)，连接E′A、E′B，求E′A＋eq \f(1,2)E′B的最小值.
如图，已知抛物线y=﹣x2＋bx＋c与x轴正半轴交于点A(3，0)，与y轴交于点B(0，3)，点P是x轴上一动点，过点P作x轴的垂线交抛物线于点C，交直线AB于点D，设P(x，0)．
(1)求抛物线的函数表达式；
(2)当0＜x＜3时，求线段CD的最大值；
(3)在△PDB和△CDB中，当其中一个三角形的面积是另一个三角形面积的2倍时，求相应x的值；
(4)过点B，C，P的外接圆恰好经过点A时，x的值为 ．(直接写出答案)
如图，在平面直角坐标系中，直线y=eq \f(1,2)x＋2与x轴交于点A，与y轴交于点C．抛物线y=ax2＋bx＋c的对称轴是x=﹣eq \f(3,2)且经过A、C两点，与x轴的另一交点为点B．
(1)①直接写出点B的坐标；②求抛物线解析式．
(2)若点P为直线AC上方的抛物线上的一点，连接PA，PC．求△PAC的面积的最大值，并求出此时点P的坐标．
(3)抛物线上是否存在点M，过点M作MN垂直x轴于点N，使得以点A、M、N为顶点的三角形与△ABC相似？若存在，求出点M的坐标；若不存在，请说明理由．
如图1，在平面直角坐标系中，抛物线C：y＝﹣eq \f(1,4)x2＋bx＋c与x轴相交于A，B两点，顶点为D，其中A(﹣4eq \r(2)，0)，B(4eq \r(2)，0)，设点F(m，0)是x轴的正半轴上一点，将抛物线C绕点F旋转180°，得到新的抛物线C'．
(1)求抛物线C的函数解析式；
(2)若抛物线C'与抛物线C在y轴的右侧有两个不同的公共点，求m的取值范围；
(3)如图2，P是第一象限内抛物线C上一点，它到两坐标轴的距离相等，点P在抛物线C'上的对应点P'，设M是C上的动点，N是C'上的动点，试探究四边形PMP'N能否成为正方形？若能，求出m的值；若不能，请说明理由．
\s 0 答案
解：(1)把点C(0，eq \r(3))代入抛物线f(x)：y＝a(x＋1)(x﹣5)中得：
﹣5a＝eq \r(3)，解得：a＝﹣eq \f(1,5)eq \r(3)，
∴y＝﹣eq \f(1,5)eq \r(3) (x＋1)(x﹣5)＝﹣eq \f(1,5)eq \r(3) (x2﹣4x﹣5)＝﹣eq \f(1,5)eq \r(3)x2＋x＋eq \r(3)，
∴抛物线f(x)的表达式为y＝﹣eq \f(1,5)eq \r(3)x2＋x＋eq \r(3)；
(2)∵点C关于x轴的对称点C′，∴C'(0，﹣eq \r(3))，
∵原抛物线沿对称轴向下平移经过点C′得到抛物线f'(x)，
∴抛物线f'(x)的解析式为：y＝﹣eq \f(1,5)eq \r(3)x2＋eq \f(4,5)eq \r(3)x﹣eq \r(3)，
∵y＝﹣eq \f(1,5)eq \r(3)x2＋eq \f(4,5)eq \r(3)x＋eq \r(3)与x轴交于点A、B(点A位于点B左边)，
令y＝0，则﹣eq \f(1,5)eq \r(3)x2＋eq \f(4,5)eq \r(3)x﹣eq \r(3)＝0，解得x1＝﹣1，x2＝5，
∴A(﹣1，0)，B(5，0)，
∵C(0，eq \r(3))，
∴OA＝1，OC＝eq \r(3)，
∴AC＝2，
∴∠ACO＝30°，∠CAO＝60°，
∵AE平分∠CAO，
∴∠CAF＝30°，
分三种情况：
①当AC＝AF＝2时，如图，设FP交y轴于G，过点F作FL⊥y轴于L，FH⊥x轴于H，过点G作GK⊥CF，交CF的延长线于K，
∴∠ACF＝∠AFC＝75°，∴∠OCF＝45°，
Rt△AFH中，FH＝eq \f(1,2)AF＝1，AH＝eq \r(3)，
∴F(eq \r(3)﹣1，1)，
∵CL＝FL＝eq \r(3)﹣1，
∴CF＝eq \r(2)FL＝eq \r(2)(eq \r(3)﹣1)，
Rt△CGK中，∠GFK＝180°﹣∠CFP＝180°﹣120°＝60°，设FK＝m，GK＝eq \r(3)m，
∵∠OCF＝45°，
∴△GCK是等腰直角三角形，
∴CK＝GK，
∴eq \r(2)(eq \r(3)﹣1)＋m＝eq \r(3)m，
∴m＝eq \r(2)，
∴CG＝eq \r(2)KG＝eq \r(6)m＝2eq \r(3)，
∴G(0，﹣eq \r(3))
可得直线PF的解析式为：y＝(2＋eq \r(3))x﹣eq \r(3)，
则，解得：，，
∴P(0，﹣eq \r(3))或(，﹣12﹣)；
②当AC＝CF时，如图，∠CAF＝∠CFA＝30°，
∴∠ACQ＝120°，
∴∠OCF＝90°，
∴F(2，eq \r(3))，
∵y＝﹣eq \f(1,5)eq \r(3)x2＋eq \f(4,5)eq \r(3)x＋eq \r(3)＝﹣eq \f(1,5)eq \r(3)(x﹣2)2＋eq \f(9,5)eq \r(3)，
∴抛物线f(x)的对称轴是：x＝2，
∴F在DF上，延长PF交y轴于G，
∵∠CFP＝120°，
∴∠GFC＝60°，
Rt△GCF中，∠CGF＝30°，
∵CF＝2，
∴CG＝2eq \r(3)，
∴OG＝3eq \r(3)，
∴G(0，3eq \r(3))，
∴GF的解析式为：y＝﹣eq \r(3)x＋3eq \r(3)，
∴，解得，，
∴P(4，﹣eq \r(3))或(5，﹣2eq \r(3))；
③当CF＝AF时，如图，∠CFA＝120°，此种情况不符合题意；
综上，当△CAQ为等腰三角形时，点P的横坐标是0或4或5或﹣eq \f(10,3)eq \r(3)﹣1．
解：(1)将点B(1，4)，E(3，0)的坐标代入抛物线的解析式得：
，解得：，
抛物线的解析式为y=﹣2x2+6x．
(2)如图1所示；
∵BD⊥DE，∴∠BDE=90°．
∴∠BDC+∠EDO=90°．
又∵∠ODE+∠DEO=90°，
∴∠BDC=∠DE0．
在△BDC和△DOE中，
，
∴△BDC≌△DEO．
∴OD=AO=1．
∴D(0，1)．
(3)如图2所示：作点B关于抛物线的对称轴的对称点B′，
连接B′D交抛物线的对称轴与点M．
∵x=﹣=eq \f(3,2)，∴点B′的坐标为(2，4)．
∵点B与点B′关于x=eq \f(3,2)对称，
∴MB=B′M．
∴DM+MB=DM+MB′．
∴当点D、M、B′在一条直线上时，MD+MB有最小值(即△BMD的周长有最小值)．
∵由两点间的距离公式可知：BD=eq \r(10)，DB′=eq \r(13)，
∴△BDM的最小值=eq \r(10)+eq \r(13)．设直线B′D的解析式为y=kx+b．
将点D、B′的坐标代入得：
，解得：k=eq \f(3,2)，b=1．
∴直线DB′的解析式为y=eq \f(3,2)x+1．
将x=eq \f(3,2)代入得：y=3eq \f(1,4)．∴M(eq \f(3,2)，3eq \f(1,4))．
(4)如图3所示：过点F作FG⊥x轴，垂足为G．
设点F(a，﹣2a2+6a)，则OG=a，FG=﹣2a2+6a．
∵S梯形DOGF=eq \f(1,2)(OD+FG)×OG=eq \f(1,2)(﹣2a2+6a+1)×a=﹣a3+3a2+eq \f(1,2)a，
S△ODA=eq \f(1,2)OD×OA=eq \f(1,2)×1×1=eq \f(1,2)，S△AGF=eq \f(1,2)AG×FG=﹣a3+4a2﹣3a，
∴S△FDA=S梯形DOGF﹣S△ODA﹣S△AGF=﹣a2+eq \f(7,2)a﹣eq \f(1,2)．
∴当a=eq \f(7,4)时，S△FDA的最大值为．
∴点P的坐标为(eq \f(7,4)，4)eq \f(3,8)．
解：(1)∵抛物线y＝ax2﹣mx＋2m﹣3经过点A(2，﹣4)，
∴4a﹣2m＋2m﹣3＝﹣4，解得：a＝﹣eq \f(1,4)；
(2)由(1)知a＝﹣eq \f(1,4)，
∴抛物线解析式为y＝﹣eq \f(1,4)x2﹣mx＋2m﹣3，
∵抛物线与y轴的公共点为(0，﹣1)，
∴2m﹣3＝﹣1，解得m＝1，
∴y＝﹣eq \f(1,4)x2﹣x﹣1，
∴Δ＝b2﹣4ac＝(﹣1)2﹣4×(﹣eq \f(1,4))×(﹣1)＝1﹣1＝0，
∴抛物线与x轴是有一个公共点，
令y＝0，则﹣eq \f(1,4)x2﹣x﹣1＝0，解得：x1＝x2＝﹣2，
∴公共点的坐标为(﹣2，0)；
(3)由(1)知，抛物线解析式为y＝﹣eq \f(1,4)x2﹣mx＋2m﹣3，
∴对称轴为直线x＝﹣2m，
①当﹣2m＜2，即m＞﹣1时，
∵a＜0，抛物线开口向下，
∴当2≤x≤4时，y随x的增大而减小，
∴当x＝2时，M＝ymax＝﹣eq \f(1,4)×22﹣2m＋2m﹣3＝﹣4，
当x＝4时，N＝ymin＝﹣eq \f(1,4)×16﹣4m＋2m﹣3＝﹣2m﹣7，
∵＝，∴＝，解得：m＝﹣，不符合题意；
②当2≤﹣2m≤4即﹣2≤m≤﹣1时，
若直线x＝2与直线x＝﹣2m接近时，
则当x＝﹣2m时y取得最大值，即M＝﹣eq \f(1,4)×(﹣2m)2﹣m×(﹣2m)＋2m﹣3＝m2＋2m﹣3，
当x＝4时，y取得最小值，即N＝﹣eq \f(1,4)×42﹣4m＋2m﹣3＝﹣2m﹣7，
∵＝，∴＝，解得：m1＝﹣eq \f(5,4)，m2＝﹣eq \f(5,2)(不合题意，舍去)；
若直线x＝4与直线x＝﹣2m接近时，
则当x＝﹣2m时y取得最大值，即M＝﹣eq \f(1,4)×(﹣2m)2﹣m×(﹣2m)＋2m﹣3＝m2＋2m﹣3，
当x＝2时，y取得最小值，即N＝﹣eq \f(1,4)×22﹣2m＋2m﹣3＝﹣4，
∵＝，∴＝，解得：m1＝，m2＝(不符合题意，舍去)；
③当﹣2m＞4即m＜﹣2时，
∵a＜0，抛物线开口向下，
∴当2≤x≤4时，y随x的增大而增大，
∴当x＝2时，N＝﹣eq \f(1,4)×22﹣2m＋2m﹣3＝﹣4，
当x＝4时，M＝﹣eq \f(1,4)×16﹣4m＋2m﹣3＝﹣2m﹣7，
∵＝，∴＝，解得：m＝﹣eq \f(7,4)(不符合题意，舍去)，
综上所述，m的值为﹣eq \f(5,4)或．
解：(1)∵顶点坐标为(1，1)，∴设抛物线解析式为y=a(x﹣1)2+1，
又抛物线过原点，∴0=a(0﹣1)2+1，解得a=﹣1，
∴抛物线解析式为y=﹣(x﹣1)2+1，
即y=﹣x2+2x，
联立抛物线和直线解析式可得
，解得或，
∴B(2，0)，C(﹣1，﹣3)；
(2)如图，分别过A、C两点作x轴的垂线，交x轴于点D、E两点，
则AD=OD=BD=1，BE=OB+OE=2+1=3，EC=3，
∴∠ABO=∠CBO=45°，即∠ABC=90°，
∴△ABC是直角三角形；
(3)假设存在满足条件的点N，
设N(x，0)，则M(x，﹣x2+2x)，∴ON=|x|，MN=|﹣x2+2x|，
由(2)在Rt△ABD和Rt△CEB中，可分别求得AB=eq \r(2)，BC=3eq \r(2)，
∵MN⊥x轴于点N∴∠ABC=∠MNO=90°，
∴当△ABC和△MNO相似时有=或=，
①当=时，则有=，即|x||﹣x+2|=eq \f(1,3)|x|，
∵当x=0时M、O、N不能构成三角形，∴x≠0，
∴|﹣x+2|=eq \f(1,3)，即﹣x+2=±eq \f(1,3)，解得x=eq \f(5,3)或x=eq \f(7,3)，
此时N点坐标为(eq \f(5,3)，0)或(eq \f(7,3)，0)；
②当=时，则有=，即|x||﹣x+2|=3|x|，
∴|﹣x+2|=3，即﹣x+2=±3，解得x=5或x=﹣1，
此时N点坐标为(﹣1，0)或(5，0)，
综上可知存在满足条件的N点，其坐标为(eq \f(5,3)，0)或(eq \f(7,3)，0)或(﹣1，0)或(5，0)．
解：(1)过点A作AH⊥x轴于点H，
∵AO＝OB＝2，∠AOB＝120°，
∴∠AOH＝60°，
∴OH＝1，AH＝eq \r(3)，
∴A点坐标为：(﹣1，eq \r(3))，B点坐标为：(2，0)，
将两点代入y＝ax2＋bx得：
，解得：a＝，
∴抛物线的表达式为：y＝eq \f(\r(3),3)x2﹣eq \f(2\r(3),3)x；
(2)如图，∵C(1，﹣eq \f(\r(3),3))，∴tan∠EOC＝eq \f(\r(3),3)，
∴∠EOC＝30°，
∴∠POC＝90°＋30°＝120°，
∵∠AOE＝120°，
∴∠AOE＝∠POC＝120°，
∵OA＝2OE，OC＝eq \f(2\r(3),3)，
∴当OP＝eq \f(1,2)OC或OP′＝2OC时，△POC与△AOE相似，
∴OP＝eq \f(\r(3),3)，OP′＝eq \f(4\r(3),3)，
∴点P坐标为(0，eq \f(\r(3),3))或(0，eq \f(4\r(3),3)).
(3)如图，取Q(eq \f(1,2)，0).连接AQ，QE′.
∵＝＝，∠QOE′＝∠BOE′，
∴△OE′Q∽△OBE′，
∴＝＝，
∴E′Q＝eq \f(1,2)BE′，
∴AE′＋eq \f(1,2)BE′＝AE′＋QE′，
∵AE′＋E′Q≥AQ，
∴E′A＋eq \f(1,2)E′B的最小值就是线段AQ的长，最小值为＝.

解：(1)∵抛物线y=﹣x2＋bx＋c与x轴正半轴交于点A(3，0)，与y轴交于点B(0，3)，
∴﹣9＋3b＋c=0，c=3，
∴b=2，
∴抛物线解析式为y=﹣x2＋2x＋3；
(2)∵A(3，0)，B(0，3)，
∴直线AB解析式为y=﹣x＋3，
∵P(x，0)．
∴D(x，﹣x＋3)，C(x，﹣x2＋2x＋3)，
∵0＜x＜3，
∴CD=﹣x2＋2x＋3﹣(﹣x＋3)=﹣x2＋3x=﹣(x﹣eq \f(3,2))2＋eq \f(9,4)，
当x=eq \f(3,2)时，CD最大=eq \f(9,4)；
(3)由(2)知，CD=|﹣x2＋3x|，DP=|﹣x＋3|
①当S△PDB=2S△CDB时，
∴PD=2CD，即：2|﹣x2＋3x|=|﹣x＋3|，
∴x=±eq \f(1,2)或x=3(舍)，
②当2S△PDB=S△CDB时，
∴2PD=CD，即：|﹣x2＋3x|=2|﹣x＋3|，
∴x=±2或x=3(舍)，
即：综上所述，x=±eq \f(1,2)或x=±2；
(4)直线AB解析式为y=﹣x＋3，
∴线段AB的垂直平分线l的解析式为y=x，
∵过点B，C，P的外接圆恰好经过点A，
∴过点B，C，P的外接圆的圆心既是线段AB的垂直平分线上，
也在线段PC的垂直平分线上，
∴，
∴x=±eq \r(3)，故答案为：±eq \r(3)
解：(1)①y=eq \f(1,2)x＋2当x=0时，y=2，当y=0时，x=﹣4，
∴C(0，2)，A(﹣4，0)，
由抛物线的对称性可知：点A与点B关于x=﹣eq \f(3,2)对称，
∴点B的坐标为1，0)．
②∵抛物线y=ax2＋bx＋c过A(﹣4，0)，B(1，0)，
∴可设抛物线解析式为y=a(x＋4)(x﹣1)，
又∵抛物线过点C(0，2)，
∴2=﹣4a∴a=﹣eq \f(1,2)∴y=﹣eq \f(1,2)x2﹣eq \f(3,2)x＋2．
(2)设P(m，﹣eq \f(1,2)m2﹣eq \f(3,2)m＋2)．过点P作PQ⊥x轴交AC于点Q，
∴Q(m，eq \f(1,2)m＋2)，
∴PQ=﹣eq \f(1,2)m2﹣eq \f(3,2)m＋2﹣(eq \f(1,2)m＋2)=﹣eq \f(1,2)m2﹣2m，
∵S△PAC=eq \f(1,2)×PQ×4=2PQ=﹣m2﹣4m=﹣(m＋2)2＋4，
∴当m=﹣2时，△PAC的面积有最大值是4，此时P(﹣2，3)．
(3)在Rt△AOC中，tan∠CAO=eq \f(1,2)在Rt△BOC中，tan∠BCO=eq \f(1,2)，
∴∠CAO=∠BCO，
∵∠BCO＋∠OBC=90°，
∴∠CAO＋∠OBC=90°，
∴∠ACB=90°，
∴△ABC∽△ACO∽△CBO，
如下图：
①当M点与C点重合，即M(0，2)时，△MAN∽△BAC；
②根据抛物线的对称性，当M(﹣3，2)时，△MAN∽△ABC；
③当点M在第四象限时，设M(n，﹣eq \f(1,2)n2﹣eq \f(3,2)n＋2)，则N(n，0)
∴MN=eq \f(1,2)n2＋eq \f(3,2)n﹣2，AN=n＋4
当AN=2MN时，MN=eq \f(1,2)AN，即eq \f(1,2)n2＋eq \f(3,2)n﹣2=eq \f(1,2)(n＋4)
整理得：n2＋2n﹣8=0解得：n1=﹣4(舍)，n2=2∴M(2，﹣3)；
当MN=2AN时，MN=2AN，即eq \f(1,2)n2＋eq \f(3,2)n﹣2=2(n＋4)，
整理得：n2﹣n﹣20=0解得：n1=﹣4(舍)，n2=5，∴M(5，﹣18)．
综上所述：存在M1(0，2)，M2(﹣3，2)，M3(2，﹣3)，M4(5，﹣18)，使得以点A、M、N为顶点的三角形与△ABC相似．
解：(1)由题意把点A(﹣4eq \r(2)，0)，B(4eq \r(2)，0)，代入y＝﹣eq \f(1,4)x2＋bx＋c中，
得：，解得：，
∴抛物线C的函数解析式为：y＝﹣eq \f(1,4)x2＋8；
(2)如图1，由题意抛物线C′的顶点坐标为(2m，﹣8)，
设抛物线C′的解析式为：y＝eq \f(1,4)(x﹣2m)2﹣8，
由，消去y得到：，
∵抛物线C′与抛物线C在y轴的右侧有两个不同的公共点，
∴，解得：4＜m＜4eq \r(2)，
∴满足条件的m的取值范围为：4＜m＜4eq \r(2)；
(3)结论：四边形PMP'N能成为正方形．
理由：情形1，如图2，作PE⊥x轴于E，MH⊥x轴于H．
由题意易知P(4，4)，
当△PFM是等腰直角三角形时，四边形PMP'N是正方形，
∴PF＝FM，∠PFM＝90°，
∵∠PEF＝∠FHM＝90°，
∴∠PFE＋∠FPE＝90°，∠PFE＋∠MFH＝90°，
在△PFE和△FMH中，
∴，
∴△PFE≌△FMH(AAS)，
∴PE＝FH＝4，EF＝HM＝4﹣m，
∴M(m＋4，m﹣4)，
∵点M在y＝﹣eq \f(1,4)x2＋8上，
∴m﹣4＝﹣eq \f(1,4)(m＋4)2＋8，解得m=﹣6+2eq \r(17)或m=﹣eq \r(17)﹣2eq \r(17)(舍)，
∴m＝﹣6＋2eq \r(17)时，四边形PMP'N是正方形．
情形2，如图，四边形PMP′N是正方形，同法可得M(m﹣4，4﹣m)，
把M(m﹣4，4﹣m)代入y＝﹣eq \f(1,4)x2＋8中，
4﹣m＝﹣eq \f(1,4)(m﹣4)2＋8，解得m＝12或m＝0(舍去)，
∴m＝12时，四边形PMP′N是正方形．
综上，四边形PMP′N能成为正方形，m＝﹣6＋2eq \r(17)或12．