2024年中考数学二轮复习 二次函数压轴题 专项提升练习六（含答案）

这是一份2024年中考数学二轮复习 二次函数压轴题 专项提升练习六（含答案），共15页。试卷主要包含了﹣3)或)或)或)等内容，欢迎下载使用。
在平面直角坐标系xOy中，已知抛物线：y＝ax2＋bx＋c交x轴于A(﹣1，0)，B(3，0)两点，与y轴交于点C(0，﹣eq \f(3,2))．
(1)求抛物线的函数解析式；
(2)如图1，点D为第四象限抛物线上一点，连接OD，过点B作BE⊥OD，垂足为E，若BE＝2OE，求点D的坐标；
(3)如图2，点M为第四象限抛物线上一动点，连接AM，交BC于点N，连接BM，记△BMN的面积为S1，△ABN的面积为S2，求的最大值．
如图，已知抛物线y＝ax2＋bx＋c(a≠0)的顶点坐标为Q(－2，－1)，且与y轴交于点C(0，3)，与x轴交于A，B两点(点A在点B的左侧)，点P是该抛物线上一动点，从点C沿抛物线向点A运动(点P与A不重合)，过点P作PD∥y轴，交直线AC于点D.
(1)求该抛物线的函数关系式；
(2)当△ADP是直角三角形时，求点P的坐标；
(3)在问题(2)的结论下，若点E在x轴上，点F在抛物线上，问是否存在以A，P，E，F为顶点的平行四边形？若存在，请直接写出点F的坐标；若不存在，请简单说明理由．
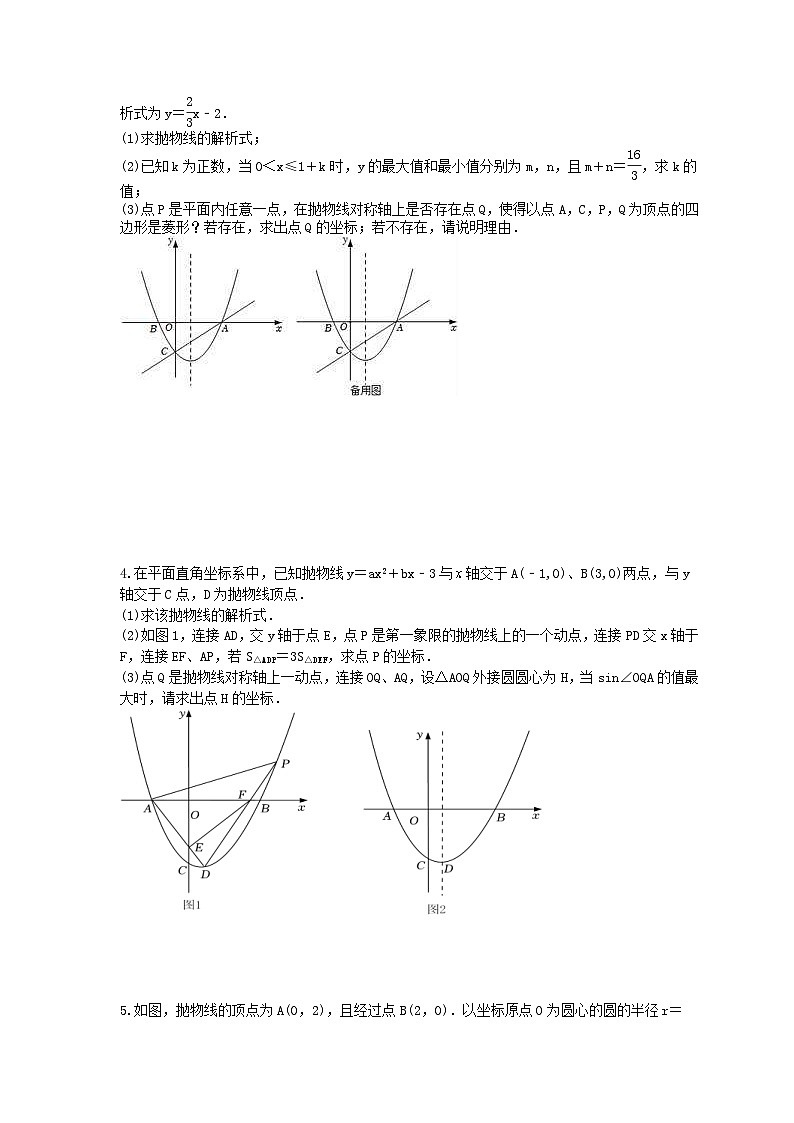
如图，抛物线y＝ax2＋bx＋c与x轴交于A，B(﹣1，0)两点，与y轴交于点C，直线AC的解析式为y＝eq \f(2,3)x﹣2．
(1)求抛物线的解析式；
(2)已知k为正数，当0＜x≤1＋k时，y的最大值和最小值分别为m，n，且m＋n＝eq \f(16,3)，求k的值；
(3)点P是平面内任意一点，在抛物线对称轴上是否存在点Q，使得以点A，C，P，Q为顶点的四边形是菱形？若存在，求出点Q的坐标；若不存在，请说明理由．
在平面直角坐标系中，已知抛物线y＝ax2＋bx﹣3与 SKIPIF 1 < 0 轴交于A(﹣1,0)、B(3,0)两点，与y轴交于C点，D为抛物线顶点．
(1)求该抛物线的解析式．
(2)如图1，连接AD，交y轴于点E，点P是第一象限的抛物线上的一个动点，连接PD交x轴于F，连接EF、AP，若S△ADP＝3S△DEF，求点P的坐标．
(3)点Q是抛物线对称轴上一动点，连接OQ、AQ，设△AOQ外接圆圆心为H，当sin∠OQA的值最大时，请求出点H的坐标．
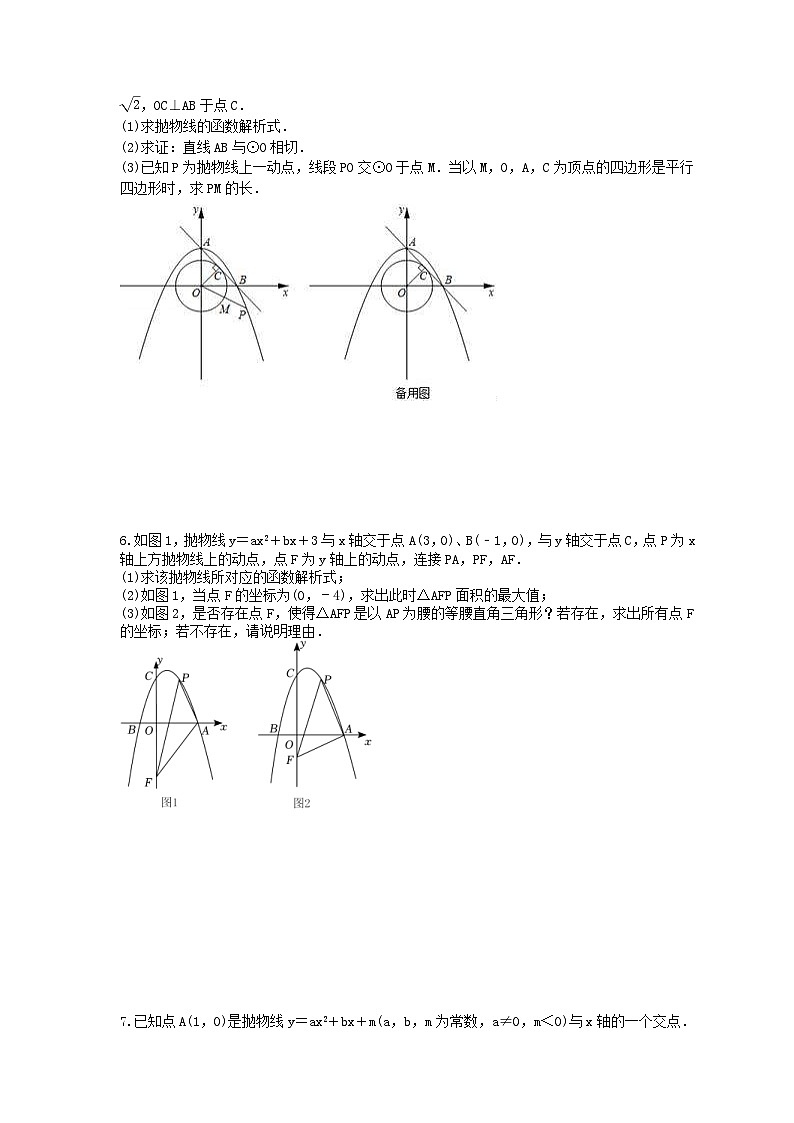
如图，抛物线的顶点为A(0，2)，且经过点B(2，0)．以坐标原点O为圆心的圆的半径r＝eq \r(2)，OC⊥AB于点C．
(1)求抛物线的函数解析式．
(2)求证：直线AB与⊙O相切．
(3)已知P为抛物线上一动点，线段PO交⊙O于点M．当以M，O，A，C为顶点的四边形是平行四边形时，求PM的长．
如图1，抛物线y＝ax2＋bx＋3与x轴交于点A(3，0)、B(﹣1，0)，与y轴交于点C，点P为x轴上方抛物线上的动点，点F为y轴上的动点，连接PA，PF，AF．
(1)求该抛物线所对应的函数解析式；
(2)如图1，当点F的坐标为(0，﹣4)，求出此时△AFP面积的最大值；
(3)如图2，是否存在点F，使得△AFP是以AP为腰的等腰直角三角形？若存在，求出所有点F的坐标；若不存在，请说明理由．
已知点A(1，0)是抛物线y＝ax2＋bx＋m(a，b，m为常数，a≠0，m＜0)与x轴的一个交点．
(Ⅰ)当a＝1，m＝﹣3时，求该抛物线的顶点坐标；
(Ⅱ)若抛物线与x轴的另一个交点为M(m，0)，与y轴的交点为C，过点C作直线l平行于x轴，E是直线l上的动点，F是y轴上的动点，EF＝2eq \r(2)．
①当点E落在抛物线上(不与点C重合)，且AE＝EF时，求点F的坐标；
②取EF的中点N，当m为何值时，MN的最小值是eq \f(\r(2),2)？
如图，已知在平面直角坐标系中，直线y=﹣eq \f(3,4)x＋6与x轴、y轴的交点分别为A、B两点，将∠OBA对折，使点O的对应点H落在直线AB上，折痕交x轴于点C．
(1)直接写出点C的坐标，并求过A、B、C三点的抛物线的解析式；
(2)若(1)中抛物线的顶点为D，在直线BC上是否存在点P，使得四边形ODAP为平行四边形？若存在，求出点P的坐标；若不存在，说明理由；
(3)若把(1)中的抛物线向左平移eq \f(7,2)个单位，则图象与x轴交于F、N(点F在点N的左侧)两点，交y轴于E点，则在此抛物线的对称轴上是否存在一点Q，使点Q到E、N两点的距离之差最大？若存在，请求出点Q的坐标；若不存在，请说明理由．
\s 0 答案
解：(1)依题意，设y＝a(x＋1)(x﹣3)，
代入C(0，﹣eq \f(3,2))得：a•1•(﹣3)＝﹣eq \f(3,2)，解得：a＝eq \f(1,2)，
∴y＝eq \f(1,2)(x＋1)(x﹣3)＝eq \f(1,2)x2﹣x﹣eq \f(3,2)；
(2)∵BE＝2OE，
设OE为x，BE＝2x，
由勾股定理得：OE2＋BE2＝OB2，
x2＋4x2＝9，解得：x1＝eq \f(3\r(5),5)，x2＝﹣eq \f(3\r(5),5)(舍)，
∴OE＝eq \f(3\r(5),5)，BE＝eq \f(6\r(5),5)，
过点E作TG平行于OB，T在y轴上，过B作BG⊥TG于G，
∴△ETO∽△OEB，
∴＝＝，
∴OE2＝OB•TE，
∴TE＝＝，
∴OT＝＝，
∴E(eq \f(3,5)，﹣eq \f(6,5))，
∴直线OE的解析式为y＝﹣2x，
∵OE的延长线交抛物线于点D，
∴，解得：x1＝1，x2＝﹣3(舍)，
当x＝1时，y＝﹣2，
∴D(1，﹣2)；
(3)如图所示，延长BC于点F，AF∥y轴，过A点作AH⊥BF于点H，作MT∥y轴交BF于点T，过M点作MG⊥BF于点J，
∵AF∥MT，
∴∠AFH＝∠MTJ，
∵AH⊥BF，MJ⊥BF，
∴∠AHF＝∠MJT＝90°，
∴△AFH∽△MJT，
∴＝，
∵S1＝eq \f(1,2)NB•MJ，S2＝eq \f(1,2)NB•AH，
∴＝＝，
设直线BC的解析式为y＝kx＋b，将B，C两点代入得，
，解得：，
∴直线BC的解析式为y＝eq \f(1,2)x﹣eq \f(3,2)，
当x＝﹣1时，y＝eq \f(1,2)•(﹣1)﹣eq \f(3,2)＝﹣2，
∴F(﹣1，﹣2)，
∴AF＝2，
设M(x，eq \f(1,2)x2﹣x﹣eq \f(3,2))，
∴MT＝eq \f(1,2)x﹣eq \f(3,2)﹣(eq \f(1,2)x2﹣x﹣eq \f(3,2))＝﹣eq \f(1,2)(x﹣eq \f(3,2))2＋eq \f(9,8)，
∴a＝﹣eq \f(1,2)＜0，
∴MTmax＝eq \f(9,8)，
∴＝＝＝＝．
解：(1)∵抛物线的顶点为Q(－2，－1)，
∴设抛物线的函数关系式为y＝a(x＋2)2－1，
将C(0，3)代入上式，得a＝1，
∴y＝(x＋2)2－1，
即y＝x2＋4x＋3.
(2)由x2＋4x＋3＝0得，x1＝－3，x2＝－1，
∴A(－3，0)，B(－1，0)．如图：
①当点A为直角顶点时，过点A作直线AC的垂线交抛物线于点P1，
∵A(－3，0)，C(0，3)，
∴直线AC的表达式为y＝x＋3.
∵AP1⊥AC，点A(－3，0)在直线AP1上，
∴直线AP1的表达式为y＝－x－3.
由eq \b\lc\{(\a\vs4\al\c1(y＝－x－3，,y＝x2＋4x＋3))得eq \b\lc\{(\a\vs4\al\c1(x＝－2，,y＝－1))
或eq \b\lc\{(\a\vs4\al\c1(x＝－3，,y＝0.))(舍去)，
∴P1(－2，－1)(即为点Q)．
②当点P2为直角顶点时，AP2⊥D2P2.
∵D2P2∥y轴，
∴AP2⊥y轴，
∴点P2与点B重合，
即P2(－1，0)．
③当点D为直角顶点时，不符合题意．
综上得，点P坐标为(－2，－1)或(－1，0)．
(3)存在，
点F的坐标为(－2－eq \r(2)，1)或(－2＋eq \r(2)，1)．
解：(1)当x＝0时，y＝﹣2，
∴点C(0，﹣2)，
当y＝0时，eq \f(2,3)x﹣2＝0，
∴x＝3，
∴点A(3，0)，
∴设y＝a(x＋1)(x﹣3)，
将点C(0，﹣2)代入得，
﹣3a＝﹣2，
∴a＝eq \f(2,3)，
∴y＝eq \f(2,3)(x＋1)(x﹣3)＝eq \f(2,3)x2﹣eq \f(4,3)x﹣2；
(2)∵抛物线的对称轴为直线：x＝1，
∵k＞0，
∴k＋1＞1，
∴当0＜x＜1＋k时，
∴当x＝1时，
n＝eq \f(2,3)(1＋1)×(1﹣3)＝﹣eq \f(8,3)，
∵m＋n＝eq \f(16,3)，
∴m＝8，
当m＝8时，eq \f(2,3)x2﹣eq \f(4,3)x﹣2＝8，
∴x1＝5，x2＝﹣3(舍去)，
∴1＋k＝5，
∴k＝4；
(3)设点Q(1，a)，
∵A(3，0)，C(0，﹣2)，
∴AQ2＝(3﹣1)2＋a2＝a2＋4，
AC2＝32＋22＝13，
CQ2＝1＋(a＋2)2＝a2＋4a＋5，
①当AQ＝AC时，
a2＋4＝13，
∴a＝±3，
∴Q1(1，3)，Q2(1，﹣3)，
当AQ＝CQ时，
a2＋4a＋5＝a2＋4，
∴a＝﹣eq \f(1,4)，
∴Q3(1，﹣eq \f(1,4))，
当AC＝CQ时，a2＋4a＋5＝13，
∴a＝﹣2±2eq \r(3)，
∴Q4(1，﹣2＋2eq \r(3))，Q5(1，﹣2﹣2eq \r(3))，
综上所述：Q(1，3)或(1．﹣3)或(1,﹣eq \f(1,4))或(1，﹣2＋2eq \r(3))或(1，﹣2﹣2eq \r(3))．
解：(1)把 SKIPIF 1 < 0 ， SKIPIF 1 < 0 代入 SKIPIF 1 < 0 中，得：
SKIPIF 1 < 0 ，解得： SKIPIF 1 < 0 ，
SKIPIF 1 < 0 抛物线解析式为 SKIPIF 1 < 0 ；
(2) SKIPIF 1 < 0 抛物线 SKIPIF 1 < 0 与 SKIPIF 1 < 0 轴交于 SKIPIF 1 < 0 、 SKIPIF 1 < 0 两点，与 SKIPIF 1 < 0 轴交于 SKIPIF 1 < 0 点， SKIPIF 1 < 0 为抛物线顶点．
SKIPIF 1 < 0 令 SKIPIF 1 < 0 ，得： SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ．
设直线 SKIPIF 1 < 0 的解析式为 SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，
SKIPIF 1 < 0 SKIPIF 1 < 0 ，解得： SKIPIF 1 < 0 ，
SKIPIF 1 < 0 直线 SKIPIF 1 < 0 的解析式为 SKIPIF 1 < 0 ，令 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ，
SKIPIF 1 < 0 SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ，
依题意，设 SKIPIF 1 < 0 ，其中 SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ，解得： SKIPIF 1 < 0 ， SKIPIF 1 < 0 (舍去)，
SKIPIF 1 < 0 ， SKIPIF 1 < 0 ；
(3)如图，作 SKIPIF 1 < 0 的外心 SKIPIF 1 < 0 ，作 SKIPIF 1 < 0 轴，则 SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ，
SKIPIF 1 < 0 在 SKIPIF 1 < 0 的垂直平分线上运动，依题意，当 SKIPIF 1 < 0 最大时，即 SKIPIF 1 < 0 最大时，
SKIPIF 1 < 0 是 SKIPIF 1 < 0 的外心，
SKIPIF 1 < 0 ，即当 SKIPIF 1 < 0 最大时， SKIPIF 1 < 0 最大，
SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，
则当 SKIPIF 1 < 0 取得最小值时， SKIPIF 1 < 0 最大，
SKIPIF 1 < 0 ，即当 SKIPIF 1 < 0 直线 SKIPIF 1 < 0 时， SKIPIF 1 < 0 取得最小值，此时 SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ，
在 SKIPIF 1 < 0 中， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，
根据对称性，则存在 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，
综上所述， SKIPIF 1 < 0 ， SKIPIF 1 < 0 或 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ．
解：(1)∵抛物线的顶点为A(0，2)，
∴可设抛物线的解析式为：y＝ax2＋2，
∵抛物线经过点B(2，0)，
∴4a＋2＝0，解得：a＝﹣eq \f(1,2)，
∴抛物线的解析式为：y＝﹣eq \f(1,2)x2＋2；
(2)证明：∵A(0，2)，B(2，0)，
∴OA＝OB＝2，
∴AB＝2eq \r(2)，
∵OC⊥AB，
∴eq \f(1,2)OAOB＝eq \f(1,2)ABOC，
∴eq \f(1,2)×2×2＝eq \f(1,2)×2eq \r(2)OC，解得：OC＝eq \r(2)，
∵⊙O的半径r＝eq \r(2)，
∴OC是⊙O的半径，
∴直线AB与⊙O相切；
(3)∵点P在抛物线y＝﹣eq \f(1,2)x2＋2上，
∴可设P(x，﹣eq \f(1,2)x2＋2)，
以M，O，A，C为顶点的四边形是平行四边形时，
可得：AC＝OM＝eq \r(2)，CM＝OA＝2，
∵点C是AB的中点，
∴C(1，1)，M(1，﹣1)，
设直线OM的解析式为y＝kx，将点M(1，﹣1)代入，得：k＝﹣1，
∴直线OM的解析式为y＝﹣x，
∵点P在OM上，
∴﹣eq \f(1,2)x2＋2＝﹣x，解得：x1＝1＋eq \r(5)，x2＝1﹣eq \r(5)，
∴y1＝﹣1﹣eq \r(5)，y2＝﹣1＋eq \r(5)，
∴P1(1＋eq \r(5)，﹣1﹣eq \r(5))，P2(1﹣eq \r(5)，﹣1＋eq \r(5))，
如图，当点P位于P1位置时，OP1＝eq \r(2)＋eq \r(10)，
∴P1M＝OP1﹣OM＝eq \r(2)＋eq \r(10)﹣eq \r(2)＝eq \r(10)，
当点P位于P2位置时，同理可得：OP2＝eq \r(10)﹣eq \r(2)，
∴P2M＝OP2﹣OM＝eq \r(10)﹣eq \r(2)﹣eq \r(2)＝eq \r(10)﹣2eq \r(2)；
综上所述，PM的长是eq \r(10)或eq \r(10)﹣2eq \r(2)．
解：(1)∵抛物线y＝ax2＋bx＋3与x轴交于点A(3，0)、B(﹣1，0)，
∴，解得：，
∴该抛物线所对应的函数解析式为y＝﹣x2＋2x＋3；
(2)如图1，过点P作PQ∥y轴交直线AF于点Q，
设直线AF的解析式为y＝kx＋d，
∵A(3，0)，F(0，﹣4)，
∴，解得：，
∴直线AF的解析式为y＝x﹣4，
设P(t，﹣t2＋2t＋3)(﹣1＜t＜3)，则Q(t，eq \f(4,3)t﹣4)，
∴PQ＝﹣t2＋2t＋3﹣(eq \f(4,3)t﹣4)＝﹣t2＋eq \f(2,3)t＋7，
∴S△AFP＝eq \f(1,2)PQ•OA＝eq \f(1,2)(﹣t2＋eq \f(2,3)t＋7)×3＝﹣eq \f(3,2)(t﹣eq \f(1,3))2＋eq \f(32,3)，
∵﹣eq \f(3,2)＜0，﹣1＜t＜3，
∴当t＝eq \f(1,3)时，△AFP面积的最大值为eq \f(32,3)；
(3)设P(m，﹣m2＋2m＋3)(﹣1＜m＜3)，F(0，n)，
∵A(3，0)，
∴OA＝3，OF＝|n|，
①当AP＝AF，∠PAF＝90°时，如图2，过点P作PD⊥x轴于点D，
则∠ADP＝90°＝∠AOF，
∴∠PAD＋∠APD＝90°，
∵∠PAD＋∠FAO＝90°，
∴∠APD＝∠FAO，
在△APD和△FAO中，
，
∴△APD≌△FAO(AAS)，
∴PD＝OA，AD＝OF，
∵PD＝﹣m2＋2m＋3，AD＝3﹣m，
∴﹣m2＋2m＋3＝3，解得：m＝0或2，
当m＝0时，P(0，3)，AD＝3，
∴OF＝3，即|n|＝3，
∵点F在y的负半轴上，
∴n＝﹣3，
∴F(0，﹣3)；
当m＝2时，P(2，3)，AD＝1，
∴OF＝1，即|n|＝1，
∵点F在y的负半轴上，
∴n＝﹣1，
∴F(0，﹣1)；
②当AP＝PF，∠APF＝90°时，如图3，过点P作PD⊥x轴于点D，PG⊥y轴于点G，
则∠PDA＝∠PDO＝∠PGF＝90°，
∵∠PDO＝∠PGF＝∠DOG＝90°，
∴四边形PDOG是矩形，
∴∠FPG＋∠FPD＝90°，
∵∠APD＋∠FPD＝∠APF＝90°，
∴∠FPG＝∠APD，
在△FPG和△APD中，
，
∴△FPG≌△APD(AAS)，
∴PG＝PD，FG＝AD，
∵PD＝﹣m2＋2m＋3，AD＝3﹣m，PG＝m，
∴﹣m2＋2m＋3＝m，
解得：m＝(舍去)或m＝，
当m＝时，P(，)，
∴FG＝AD＝3﹣m＝3﹣＝，
∴F(0，eq \r(13)﹣2)；
综上所述，点F的坐标为(0，﹣3)或(0，﹣1)或(0，eq \r(13)﹣2)．
解：(Ⅰ)当a＝1，m＝﹣3时，抛物线的解析式为y＝x2＋bx﹣3．
∵抛物线经过点A(1，0)，
∴0＝1＋b﹣3，解得b＝2，
∴抛物线的解析式为y＝x2＋2x﹣3．
∵y＝x2＋2x﹣3＝(x＋1)2﹣4，
∴抛物线的顶点坐标为(﹣1，﹣4)．
(Ⅱ)①∵抛物线y＝ax2＋bx＋m经过点A(1，0)和M(m，0)，m＜0，
∴0＝a＋b＋m，0＝am2＋bm＋m，即am＋b＋1＝0．
∴a＝1，b＝﹣m﹣1．
∴抛物线的解析式为y＝x2﹣(m＋1)x＋m．
根据题意得，点C(0，m)，点E(m＋1，m)，
过点A作AH⊥l于点H，由点A(1，0)，得点H(1，m)．
在Rt△EAH中，EH＝1﹣(m＋1)＝﹣m，HA＝0﹣m＝﹣m，∴AE＝﹣eq \r(2)m，
∵AE＝EF＝2eq \r(2)，
∴﹣eq \r(2)m＝2eq \r(2)，解得m＝﹣2．
此时，点E(﹣1，﹣2)，点C(0，﹣2)，有EC＝1．
∵点F在y轴上，
∴在Rt△EFC中，CF＝eq \r(7)．
∴点F的坐标为(0，﹣2﹣eq \r(7))或(0，﹣2＋eq \r(7))．
②由N是EF的中点，连接CN，CM，得CN＝eq \f(1,2)EF＝eq \r(2)．
根据题意，点N在以点C为圆心、eq \r(2)为半径的圆上，
由点M(m，0)，点C(0，m)，得MO＝﹣m，CO＝﹣m，
∴在Rt△MCO中，MC＝﹣eq \r(2)m．
当MC≥eq \r(2)，即m≤﹣1时，满足条件的点N在线段MC上．
MN的最小值为MC﹣NC＝﹣eq \r(2)m﹣eq \r(2)＝eq \f(\r(2),2)，解得m＝﹣eq \f(3,2)；
当MC＜eq \r(2)，即﹣1＜m＜0时，满足条件的点N落在线段CM的延长线上，MN的最小值为NC﹣MC＝eq \r(2)﹣(﹣eq \r(2)m)＝eq \f(\r(2),2)，解得m＝﹣eq \f(1,2)．
∴当m的值为﹣eq \f(3,2)或﹣eq \f(1,2)时，MN的最小值是eq \f(\r(2),2)．
解：(1)连接CH 由轴对称得CH⊥AB，BH=BO，CH=CO
∴在△CHA中由勾股定理，得AC2=CH2＋AH2
∵直线y=﹣eq \f(3,4)x＋6与x轴、y轴的交点分别为A、B两点
∴当x=0时，y=6，当y=0时，x=8
∴B(0，6)，A(8，0)
∴OB=6，OA=8，
在Rt△AOB中，由勾股定理，得AB=10
设C(a，0)，∴OC=a
∴CH=a，AH=4，AC=8﹣a，
在Rt△AHC中，由勾股定理，得
(8﹣a)2=a2＋42解得a=3
C(3，0)
设抛物线的解析式为：y=ax2＋bx＋c，由题意，
得解得：
∴抛物线的解析式为：y=eq \f(1,4)x2﹣eq \f(11,4)x＋6
∴y=eq \f(1,4)(x﹣eq \f(11,2))2﹣eq \f(25,16)
(2)由(1)的结论，得D(eq \f(11,2)，﹣eq \f(25,16))∴DF=eq \f(25,16)
设BC的解析式为：y=kx＋b，则有
解得
直线BC的解析式为：y=﹣2x＋6
设存在点P使四边形ODAP是平行四边形，P(m，n)作PE⊥OA于E，HD交OA于F．
∴∠PEO=∠AFD=90°，PO=DA，PO∥DA
∴∠POE=∠DAF
∴△OPE≌△ADF
∴PE=DF=eq \f(25,16)
∴P(eq \f(5,2)，eq \f(25,16))
当x=eq \f(5,2)时，y=﹣2×eq \f(5,2)＋6=1≠eq \f(25,16)
∴点P不再直线BC上，即直线BC上不存在满足条件的点P．
(3)由题意得，平移后的解析式为：y=eq \f(1,4)(x﹣2)2﹣eq \f(25,16)∴对称轴为：x=2，
当x=0时，y=﹣当y=0时，0=eq \f(1,4)(x﹣2)2﹣eq \f(25,16)
解得：x1=﹣eq \f(1,2)，x2=eq \f(9,2).
∵F在N的左边F(﹣eq \f(1,2)，0)，E(0，﹣)，N(eq \f(9,2)，0)
连接EF交x=2于Q，设EF的解析式为：y=kx＋b，则有
解得：∴EF的解析式为：y=﹣x﹣
∴解得：∴Q(2，)．