

所属成套资源:2024年中考数学二轮复习 二次函数压轴题 专项提升练习 (含答案)
2024年中考数学二轮复习 二次函数压轴题 专项提升练习06(含答案)
展开
这是一份2024年中考数学二轮复习 二次函数压轴题 专项提升练习06(含答案),共15页。试卷主要包含了如图2,连接BE,等内容,欢迎下载使用。
如图,抛物线y=ax2+eq \f(3,2)x+c与x轴交于点A,B,与y轴交于点C,已知A,C两点坐标分别是A(1,0),C(0,﹣2),连接AC,BC.
(1)求抛物线的表达式和AC所在直线的表达式;
(2)将△ABC沿BC所在直线折叠,得到△DBC,点A的对应点D是否落在抛物线的对称轴上?若点D在对称轴上,请求出点D的坐标;若点D不在对称轴上,请说明理由;
(3)若点P是抛物线位于第三象限图象上的一动点,连接AP交BC于点Q,连接BP,△BPQ的面积记为S1,△ABQ的面积记为S2,求的值最大时点P的坐标.
如图,抛物线y=x2+bx+c经过点A(﹣1,0),B(0,﹣2),并与x轴交于点C,点M是抛物线对称轴l上任意一点(点M,B,C三点不在同一直线上).
(1)求该抛物线所表示的二次函数的表达式;
(2)在抛物线上找出两点P1,P2,使得△MP1P2与△MCB全等,并求出点P1,P2的坐标;
(3)在对称轴上是否存在点Q,使得∠BQC为直角,若存在,作出点Q(用尺规作图,保留作图痕迹),并求出点Q的坐标.
如图,抛物线y=ax2+bx+4经过点A(﹣2,0),点B(4,0),与y轴交于点C,过点C作直线CD∥x轴,与抛物线交于点D,作直线BC,连接AC.
(1)求抛物线的函数表达式,并用配方法求抛物线的顶点坐标;
(2)E是抛物线上的点,求满足∠ECD=∠ACO的点E的坐标;
(3)点M在y轴上,且位于点C的上方,点N在直线BC上,点P为直线BC上方抛物线上一点,若以点C,M,N,P为顶点的四边形是菱形,求菱形的边长.
如图,在平面直角坐标系中,抛物线y=ax2+bx+c与x轴交于点A(﹣2,0),B(4,0),与直线y=eq \f(3,2)x+3交于y轴上的点C,直线y=﹣eq \f(3,2)x+3与x轴交于点D.
(1)求该抛物线的解析式;
(2)点P是抛物线上第一象限内的一一个动点,连接PC、PD,当△PCD的面积最大时,求点P的坐标;
(3)将抛物线的对称轴向左平移3个长度单位得到直线l,点E是直线 SKIPIF 1 < 0 上一点,连接OE、BE,若直线l上存在使sin∠BEO最大的点E,请直接写出满足条件的点E的坐标;若不存在,请说明理由.
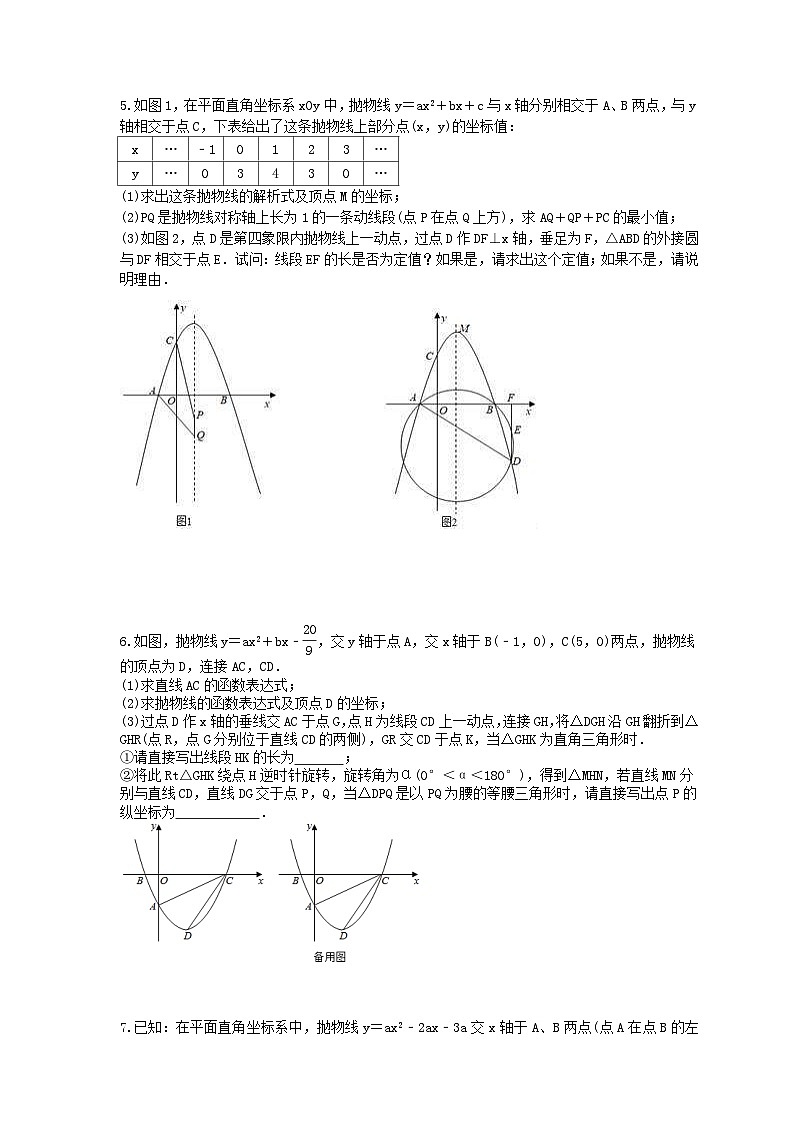
如图1,在平面直角坐标系xOy中,抛物线y=ax2+bx+c与x轴分别相交于A、B两点,与y轴相交于点C,下表给出了这条抛物线上部分点(x,y)的坐标值:
(1)求出这条抛物线的解析式及顶点M的坐标;
(2)PQ是抛物线对称轴上长为1的一条动线段(点P在点Q上方),求AQ+QP+PC的最小值;
(3)如图2,点D是第四象限内抛物线上一动点,过点D作DF⊥x轴,垂足为F,△ABD的外接圆与DF相交于点E.试问:线段EF的长是否为定值?如果是,请求出这个定值;如果不是,请说明理由.
如图,抛物线y=ax2+bx﹣eq \f(20,9),交y轴于点A,交x轴于B(﹣1,0),C(5,0)两点,抛物线的顶点为D,连接AC,CD.
(1)求直线AC的函数表达式;
(2)求抛物线的函数表达式及顶点D的坐标;
(3)过点D作x轴的垂线交AC于点G,点H为线段CD上一动点,连接GH,将△DGH沿GH翻折到△GHR(点R,点G分别位于直线CD的两侧),GR交CD于点K,当△GHK为直角三角形时.
①请直接写出线段HK的长为 ;
②将此Rt△GHK绕点H逆时针旋转,旋转角为α(0°<α<180°),得到△MHN,若直线MN分别与直线CD,直线DG交于点P,Q,当△DPQ是以PQ为腰的等腰三角形时,请直接写出点P的纵坐标为 .
已知:在平面直角坐标系中,抛物线y=ax2﹣2ax﹣3a交x轴于A、B两点(点A在点B的左边),交y轴负半轴于点C.
(1)则点A的坐标为 ,点B的坐标为 .
(2)如图1,过点A的直线y=ax+a交y轴正半轴于点F,交抛物线于点D,过点B作BE∥y轴交AD于E,求证:AF=DE.
(3)如图2,直线DE:y=kx+b与抛物线只有一个交点D,与对称轴交于点E,对称轴上存在点F,满足DF=FE.若a=1,求点F坐标.
如图,在平面直角坐标系中,直线y=kx﹣4k+4与抛物线y=eq \f(1,4)x2﹣x交于A、B两点.
(1)直线总经过定点,请直接写出该定点的坐标;
(2)点P在抛物线上,当k=﹣eq \f(1,2)时,解决下列问题:
①在直线AB下方的抛物线上求点P,使得△PAB的面积等于20;
②连接OA,OB,OP,作PC⊥x轴于点C,若△POC和△ABO相似,请直接写出点P的坐标.
\s 0 答案
解:(1)∵抛物线y=ax2+eq \f(3,2)x+c过点A(1,0),C(0,﹣2),
∴,解得:.
∴抛物线的表达式为y=eq \f(1,2)x2+eq \f(3,2)x﹣2.
设直线AC的表达式为y=kx+b,则
,解得:.
∴直线AC的表达式为y=2x﹣2.
(2)点D不在抛物线的对称轴上,理由是:
∵抛物线的表达式为y=eq \f(1,2)x2+eq \f(3,2)x﹣2,
∴点B坐标为(﹣4,0).
∵OA=1,OC=2,
∴.
又∵∠AOC=∠COB=90°,
∴△AOC∽△COB.
∴∠ACO=∠CBO.
∴∠ACO+∠BCO=∠OBC+∠BCO=90°,
∴AC⊥BC.
∴将△ABC沿BC所在直线折叠,点D一定落在直线AC上,
延长AC至D,使DC=AC,过点D作DE⊥y轴交y轴于点E,如图1.
又∵∠ACO=∠DCE,
∴△ACO≌△DCE(AAS).
∴DE=AO=1,则点D横坐标为﹣1,
∵抛物线的对称轴为直线x=﹣eq \f(3,2).
故点D不在抛物线的对称轴上.
(3)设过点B、C的直线表达式为y=px+q,
∵C(0,﹣2),B(﹣4,0),
∴,解得:.
∴过点B、C的直线解析式为y=﹣eq \f(1,2)x﹣2.
过点A作x轴的垂线交BC的延长线于点M,点M坐标为(1,﹣eq \f(5,2)),
过点P作x轴的垂线交BC于点N,垂足为H,如图2.
设点P坐标为(m,eq \f(1,2)m2+eq \f(3,2)m﹣2),则点N坐标为(m,﹣eq \f(1,2)m﹣2),
∴PN=﹣eq \f(1,2)m﹣2﹣(eq \f(1,2)m2+eq \f(3,2)m﹣2)=﹣eq \f(1,2)m2﹣2m,
∵PN∥AM,
∴△AQM∽△PQN.
∴.
若分别以PQ、AQ为底计算△BPQ和△BAQ的面积(同高不等底),
则△BPQ与△BAQ的面积比为,即.
∴==.
∵﹣eq \f(1,5)<0,
∴当m=﹣2时,的最大值为,此时点P坐标为(﹣2,﹣3).
解:(1)把A(﹣1,0),B(0,﹣2)代入抛物线y=x2+bx+c中得:
,解得:,
∴抛物线所表示的二次函数的表达式为:y=x2﹣x﹣2;
(2)如图1,P1与A重合,P2与B关于l对称,
∴MB=P2M,P1M=CM,P1P2=BC,
∴△P1MP2≌△CMB,
∵y=x2﹣x﹣2=(x﹣eq \f(1,2))2﹣eq \f(9,4),
此时P1(﹣1,0),
∵B(0,﹣2),对称轴:直线x=eq \f(1,2),
∴P2(1,﹣2);
如图2,MP2∥BC,且MP2=BC,
此时,P1与C重合,
∵MP2=BC,MC=MC,∠P2MC=∠BP1M,
∴△BMC≌△P2P1M,
∴P1(2,0),
由点B向右平移eq \f(1,2)个单位到M,可知:点C向右平移eq \f(1,2)个单位到P2,
当x=eq \f(5,2)时,y=(eq \f(5,2)﹣eq \f(1,2))2﹣eq \f(9,4)=eq \f(7,4),
∴P2(eq \f(5,2),eq \f(7,4));
如图3,构建▱MP1P2C,可得△P1MP2≌△CBM,此时P2与B重合,
由点C向左平移2个单位到B,可知:点M向左平移2个单位到P1,
∴点P1的横坐标为﹣eq \f(3,2),
当x=﹣eq \f(3,2)时,y=(﹣eq \f(3,2)﹣eq \f(1,2))2﹣eq \f(9,4)=4﹣eq \f(9,4)=eq \f(7,4),
∴P1(﹣eq \f(3,2),eq \f(7,4)),P2(0,﹣2);
(3)如图3,存在,作法:以BC为直径作圆交对称轴l于两点Q1、Q2,
则∠BQ1C=∠BQ2C=90°;
过Q1作DE⊥y轴于D,过C作CE⊥DE于E,
设Q1(eq \f(1,2),y)(y>0),
易得△BDQ1∽△Q1EC,
∴,∴=,
y2+2y﹣eq \f(3,4)=0,解得:y1=﹣1﹣eq \f(\r(7),2)(舍),y2=﹣1+eq \f(\r(7),2),
∴Q1(eq \f(1,2),﹣1+eq \f(\r(7),2)),同理可得:Q2(eq \f(1,2),﹣1﹣eq \f(\r(7),2));
综上所述,点Q的坐标是:(eq \f(1,2),﹣1+eq \f(\r(7),2)),或(eq \f(1,2),﹣1﹣eq \f(\r(7),2)).
解:(1)∵抛物线y=ax2+bx+c的图象经过点A(﹣2,0),点B(4,0),
∴得,∴解得,
∴抛物线解析式为y=﹣x2+x+4,
∵,
∴抛物线的顶点坐标为(1,eq \f(9,2));
(2)如图1,
设满足条件的点在抛物线上:
①当点E位于直线CD下方时,过点E作EF⊥直线CD,垂足为F.
则F(t,4),CF=t,,
根据题意,当∠ECD=∠ACO时,tan∠ACO=tan∠ECD,
即,∴,解得t1=0(舍去),t2=3,
∴;
②当点E'位于直线CD上方时,过点E'作E'F'⊥直线CD,垂足为F'.
则F'(s,4),CF'=s,E'F'=﹣eq \f(1,2)s2+s+4﹣4=﹣eq \f(1,2)s2+s,
根据题意,当∠ECD=∠ACO时,tan∠ACO=tan∠ECD,
即,∴,解得s1=0(舍去),s2=1.
∴E’(1,eq \f(9,2)),
所以,点E的坐标为(3,eq \f(5,2))或(1,eq \f(9,2));
(3)①CM为菱形的边,如图2,在第一象限内取点P′,过点P′作P′N′∥y轴,交BC于N′,过点P′作P′M′∥BC,交y轴于M′,
∴四边形CM′P′N′是平行四边形,
∵四边形CM′P′N′是菱形,
∴P′M′=P′N′,
过点P′作P′Q′⊥y轴,垂足为Q′,
∵OC=OB,∠BOC=90°,
∴∠OCB=45°,
∴∠P′M′C=45°,
设点P′(m,﹣eq \f(1,2)m2+m+4),
在Rt△P′M′Q′中,P′Q′=m,P′M′=eq \r(2)m,
∵B(4,0),C(0,4),
∴直线BC的解析式为y=﹣x+4,
∵P′N′∥y轴,
∴N′(m,﹣m+4),
∴P′N′=﹣eq \f(1,2)m2+m+4﹣(﹣m+4)=﹣eq \f(1,2)m2+2m,
∴eq \r(2)m=﹣eq \f(1,2)m2+2m,∴m=0(舍)或m=4﹣2eq \r(2),
菱形CM′P′N′的边长为eq \r(2)(4﹣2eq \r(2))=4eq \r(2)﹣4.
②CM为菱形的对角线,如图3,
在第一象限内抛物线上取点P,过点P作PM∥BC,
交y轴于点M,连接CP,过点M作MN∥CP,交BC于N,
∴四边形CPMN是平行四边形,连接PN交CM于点Q,
∵四边形CPMN是菱形,
∴PQ⊥CM,∠PCQ=∠NCQ,
∵∠OCB=45°,
∴∠NCQ=45°,
∴∠PCQ=45°,
∴∠CPQ=∠PCQ=45°,
∴PQ=CQ,
设点P(n,﹣eq \f(1,2)n2+n+4),
∴CQ=n,OQ=n+4,
∴n+4=﹣eq \f(1,2)n2+n+4,∴n=0(舍),
∴此种情况不存在.
综上,菱形的边长为4eq \r(2)﹣4.
解:(1)用交点式函数表达式得: SKIPIF 1 < 0 ,
当 SKIPIF 1 < 0 时, SKIPIF 1 < 0 ,则 SKIPIF 1 < 0 ,即 SKIPIF 1 < 0 ,解得: SKIPIF 1 < 0 .
则函数的表达式为 SKIPIF 1 < 0 ;
(2) SKIPIF 1 < 0 ,令 SKIPIF 1 < 0 ,则 SKIPIF 1 < 0 ,即点 SKIPIF 1 < 0 ,
连接 SKIPIF 1 < 0 ,设点 SKIPIF 1 < 0 ,
SKIPIF 1 < 0
SKIPIF 1 < 0
SKIPIF 1 < 0 ,
SKIPIF 1 < 0 ,
SKIPIF 1 < 0 有最大值,此时点 SKIPIF 1 < 0 ;
(3)如图,经过点 SKIPIF 1 < 0 、 SKIPIF 1 < 0 的圆 SKIPIF 1 < 0 与直线 SKIPIF 1 < 0 相切于点 SKIPIF 1 < 0 ,此时, SKIPIF 1 < 0 最大,
过圆心 SKIPIF 1 < 0 作 SKIPIF 1 < 0 轴于点 SKIPIF 1 < 0 ,则 SKIPIF 1 < 0 , SKIPIF 1 < 0 ,
SKIPIF 1 < 0 ,过点 SKIPIF 1 < 0 的坐标为 SKIPIF 1 < 0 , SKIPIF 1 < 0 ;
同样当点 SKIPIF 1 < 0 在 SKIPIF 1 < 0 轴的下方时,其坐标为 SKIPIF 1 < 0 ;
故点 SKIPIF 1 < 0 的坐标为 SKIPIF 1 < 0 , SKIPIF 1 < 0 或 SKIPIF 1 < 0 .
解:(1)根据表格可得出A(﹣1,0),B(3,0),C(0,3),
设抛物线解析式为y=a(x+1)(x﹣3),
将C(0,3)代入,得:3=a(0+1)(0﹣3),解得:a=﹣1,
∴y=﹣(x+1)(x﹣3)=﹣x2+2x+3=﹣(x﹣1)2+4,
∴该抛物线解析式为y=﹣x2+2x+3,顶点坐标为M(1,4);
(2)如图1,将点C沿y轴向下平移1个单位得C′(0,2),连接BC′交抛物线对称轴x=1于点Q′,过点C作CP′∥BC′,交对称轴于点P′,连接AQ′,
∵A、B关于直线x=1对称,
∴AQ′=BQ′,
∵CP′∥BC′,P′Q′∥CC′,
∴四边形CC′Q′P′是平行四边形,
∴CP′=C′Q′,Q′P′=CC′=1,
在Rt△BOC′中,BC′=eq \r(13),
∴AQ′+Q′P′+P′C=BQ′+C′Q′+Q′P′=BC′+Q′P′=eq \r(13)+1,
此时,C′、Q′、B三点共线,BQ′+C′Q′的值最小,
∴AQ+QP+PC的最小值为eq \r(13)+1;
(3)线段EF的长为定值1.如图2,连接BE,
设D(t,﹣t2+2t+3),且t>3,
∵EF⊥x轴,
∴DF=﹣(﹣t2+2t+3)=t2﹣2t﹣3,
∵F(t,0),
∴BF=OF﹣OB=t﹣3,AF=t﹣(﹣1)=t+1,
∵四边形ABED是圆内接四边形,
∴∠DAF+∠BED=180°,
∵∠BEF+∠BED=180°,
∴∠DAF=∠BEF,
∵∠AFD=∠EFB=90°,
∴△AFD∽△EFB,
∴=,∴=,∴EF===1,
∴线段EF的长为定值1.
解:(1)设直线AC的函数表达式为:y=kx+c,
∵抛物线y=ax2+bx﹣eq \f(20,9),交y轴于点A,∴A(0,﹣eq \f(20,9)),
将A(0,﹣eq \f(20,9)),C(5,0)分别代入y=kx+c,
得:,解得:,
∴直线AC的函数表达式为:y=eq \f(4,9)x﹣eq \f(20,9),
(2)∵抛物线y=ax2+bx﹣eq \f(20,9)经过B(﹣1,0),C(5,0)两点,
∴,解得:,
∴抛物线的解析式为y=eq \f(4,9)x2﹣x﹣eq \f(20,9),
∵y=eq \f(4,9)x2﹣eq \f(16,9)x﹣eq \f(20,9)=eq \f(4,9)(x﹣2)2﹣4,
∴顶点D的坐标为(2,﹣4);
(3)①如图1,∵△GHK为直角三角形,且点R,点G分别位于直线CD的两侧,
∴∠GHK=90°或∠HGK=90°或∠GKH=90°,
当∠GHK=90°时,∠GHD=90°,点R落在直线DC上,不符合题意,
当∠HGK=90°时,∠DGH=∠HGK=90°,点R,点G位于直线CD的同侧,不符合题意,
当∠GKH=90°时,点R,点G分别位于直线CD的两侧,符合题意,
∴∠GKH=90°,∠DGH=∠RGH,
过点H作HL⊥DG于点L,则HL=HK,
∵D(2,﹣4),DG⊥x轴,
∴G(2,﹣eq \f(4,3)),F(2,0),
∴DG=﹣eq \f(4,3)﹣(﹣4)=eq \f(8,3),CF=5﹣2=3,DF=4,
∴CD=5,
∵∠DFC=∠GKH=90°,∠GDK=∠CDF,
∴△GDK∽△CDF,
∴==,即==,
∴GK=,DK=,
∵S△GKH+S△GDH=S△GDK,
∴××HK+××HL=××,
故答案为:eq \f(4,5);
②∵△DPQ是以PQ为腰的等腰三角形,
∴PQ=DQ或PQ=DP,
当PQ=DQ时,如图2,由旋转知:点H到PQ、DQ的距离相等,
∴QH⊥DP,DH=HP,
由①知HL=HK=eq \f(4,5),
∵HL∥CF,
∴=,即=,
∴DL=,
∴L的纵坐标为﹣4=﹣,即H的纵坐标为﹣,
∵H为D、P的中点,
∴P的纵坐标为﹣,
当PQ=DP时,如图3,点P为DQ的垂直平分线与CD的交点,
∵H(,﹣),
∴经过点H平行MN的直线为y=﹣eq \f(4,3)x+eq \f(4,5),
∵点H到直线MN的距离为eq \f(4,5),
∴直线MN的解析式为y=﹣eq \f(4,3)x﹣eq \f(8,15),
∵直线CD的解析式为y=eq \f(4,3)x﹣eq \f(20,3),
∴P(,﹣);
综上所述,点P的纵坐标为﹣或﹣.
解:(1)令y=0,得ax2﹣2ax﹣3a=0
即x2﹣2x﹣3=0得x1=3,x2=﹣1
∴A(﹣1,0)B(3,0)
(2)过E,D分别作x轴,y轴的平行线,交于H.
令ax+a=ax2﹣2ax﹣3a得ax2﹣3ax﹣4a=0,
∴x2﹣3x﹣4=0
∴x1=4,x2=﹣1
∴xD=4
∴EH=AO=1
=∠AOF=∠EHD,∠FAO=∠DEH
∴△FAO≌△DEH
∴AF=DE
(3)令x^{2}﹣2 x﹣3=kx+b
得x2﹣(2+k)x﹣3﹣b=0
(2+k)2+4(3+b)=0
∴
=
=
∴
∴
=
∴,
∴
=
=
∴
=
=
∵EF=DF
∴
整理得
∴yF=﹣eq \f(15,4)
F的坐标为(1,﹣eq \f(15,4))
解:(1)∵y=kx﹣4k+4=k(x﹣4)+4,
即k(x﹣4)=y﹣4,
而k为任意不为0的实数,
∴x﹣4=0,y﹣4=0,解得x=4,y=4,
∴直线过定点(4,4);
(2)当k=﹣eq \f(1,2)时,直线解析式为y=﹣eq \f(1,2)x+6,
解方程组得或,
则A(6,3)、B(﹣4,8);
①如图1,作PQ∥y轴,交AB于点Q,
设P(x,eq \f(1,4)x2﹣x),则Q(x,﹣eq \f(1,2)x+6),
∴PQ=(﹣eq \f(1,2)x+6)﹣(eq \f(1,4)x2﹣x)=﹣eq \f(1,4)(x﹣1)2+eq \f(25,4),
∴S△PAB=eq \f(1,2)(6+4)×PQ=﹣eq \f(5,4)(x﹣1)2+=20,解得x1=﹣2,x2=4,
∴点P的坐标为(4,0)或(﹣2,3);
②设P(x,eq \f(1,4)x2﹣x),如图2,
由题意得:AO=3eq \r(5),BO=4eq \r(5),AB=5eq \r(5),
∵AB2=AO2+BO2,
∴∠AOB=90°,
∵∠AOB=∠PCO,
∴当=时,△CPO∽△OAB,
即=,整理得4|eq \f(1,4)x2﹣x|=3|x|,
解方程4(eq \f(1,4)x2﹣x)=3x得x1=0(舍去),x2=7,此时P点坐标为(7,eq \f(21,4));
解方程4(eq \f(1,4)x2﹣x)=﹣3x得x1=0(舍去),x2=1,此时P点坐标为(1,﹣eq \f(3,4));
当=时,△CPO∽△OBA,即=,整理得3|eq \f(1,4)x2﹣x|=4|x|,
解方程3(eq \f(1,4)x2﹣x)=4x得x1=0(舍去),x2=,此时P点坐标为(,);
解方程3(eq \f(1,4)x2﹣x)=﹣4x得x1=0(舍去),x2=﹣eq \f(4,3),此时P点坐标为(﹣eq \f(4,3),)
综上所述,点P的坐标为:(7,eq \f(21,4))或(1,﹣eq \f(3,4))或(﹣eq \f(4,3),)或(,).
x
…
﹣1
0
1
2
3
…
y
…
0
3
4
3
0
…
相关试卷
这是一份2024年中考数学二轮复习 二次函数压轴题 专项提升练习10(含答案),共12页。
这是一份2024年中考数学二轮复习 二次函数压轴题 专项提升练习09(含答案),共14页。试卷主要包含了以PQ,QM为边作矩形PQMN等内容,欢迎下载使用。
这是一份2024年中考数学二轮复习 二次函数压轴题 专项提升练习08(含答案),共14页。试卷主要包含了B两点,与y轴交于点D.等内容,欢迎下载使用。









