



- 人教A版高中数学(必修第二册)同步讲义第二十三讲 第七章 复数 章节验收测评卷(2份打包,原卷版+教师版) 试卷 0 次下载
- 人教A版高中数学(必修第二册)同步讲义第24讲 8.1基本立体图形(第1课时 棱柱、棱锥、棱台的结构特征)(2份打包,原卷版+教师版) 试卷 1 次下载
- 人教A版高中数学(必修第二册)同步讲义第26讲 8.2 立体图形的直观图(2份打包,原卷版+教师版) 试卷 0 次下载
- 人教A版高中数学(必修第二册)同步讲义第30讲 8.4.2 空间点、直线、平面之间的位置关系(2份打包,原卷版+教师版) 试卷 1 次下载
- 人教A版高中数学(必修第二册)同步讲义第40讲 第八章 立体几何初步 章末题型大总结(2份打包,原卷版+教师版) 试卷 3 次下载
高中数学人教A版 (2019)必修 第二册8.1 基本立体图形优秀第2课时课后复习题
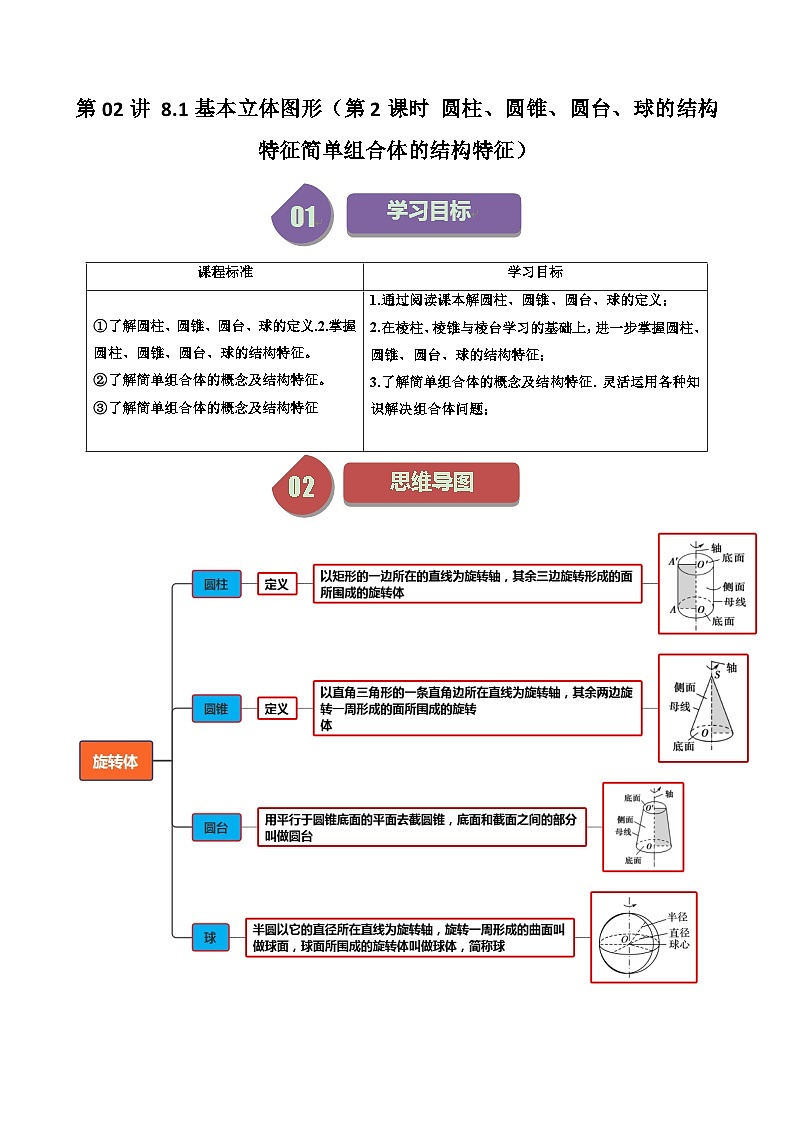
展开知识点01:圆柱
(1)圆柱的定义
以矩形的一边所在的直线为旋转轴,其余三边旋转形成的面所围成的旋转体
圆柱的轴:旋转轴
圆柱的底面:垂直于轴的边旋转而成的圆面
圆柱的侧面:平行于轴的边旋转而成的曲面
圆柱侧面的母线:无论旋转到什么位置,平行于轴的边
(2)圆柱的图形
(3)圆柱的表示
圆柱用表示它的轴的字母表示,如图,圆柱
【即学即练1】1(2024上·上海·高二上海师大附中校考期末)用一个平面截如图所示圆柱体,截面的形状不可能是( )
A. B.
C. D.
【答案】D
【详解】解:
对于选项A:当截面与轴截面垂直时,得到的截面形状是圆;
对于选项B:当截面与轴截面平行时,得到的截面形状是长方形;
对于选项C:当截面与轴截面斜交时,得到的截面形状是椭圆;
对于选项D:截面的形状不可能是等腰梯形;
故选:D
知识点02:圆锥
(1)圆锥的定义
以直角三角形的一条直角边所在直线为旋转轴,其余两边旋转一周形成的面所围成的旋转体
轴:旋转轴叫做圆锥的轴
底面:垂直于轴的边旋转而成的圆面
侧面:直角三角形的斜边旋转而成的曲面
母线:无论旋转到什么位置,不垂直于轴的边
锥体:棱锥和圆锥统称为锥体
(2)圆锥的图形
(3)圆锥的表示
用表示它的轴的字母表示,如图,圆锥
【即学即练2】(2024·全国·高三专题练习)给出下列命题:
①在圆柱的上、下底面的圆周上各取一点,则这两点的连线是圆柱的母线;
②直角三角形绕其任一边所在直线旋转一周所形成的几何体都是圆锥;
③棱台的上、下底面可以不相似,但侧棱长一定相等.
其中正确命题的个数是( )
A.B.C.D.
【答案】A
【详解】①不一定,只有当这两点的连线平行于轴时才是母线;
②不一定,当以斜边所在直线为旋转轴时,其余两边旋转形成的面所围成的几何体不是圆锥,如图所示,它是由两个同底圆锥组成的几何体;
③错误,棱台的上、下底面相似且是对应边平行的多边形,各侧棱延长线交于一点,但是侧棱长不一定相等.
故选:A.
知识点03:圆台
(1)圆台的定义
用平行于圆锥底面的平面去截圆锥,底面和截面之间的部分叫做圆台
轴:圆锥的轴
底面:圆锥的底面和截面
侧面:圆锥的侧面在底面与截面之间的部分
母线:圆锥的母线在底面与截面之间的部分
台体:棱台和圆台统称为台体
(2)圆台的图形
(3)圆台的表示
用表示它的轴的字母表示,如图,圆台
【即学即练3】(2024上·上海青浦·高二上海市朱家角中学校考期末)已知某圆台上底面和下底面的半径分别为1和2,母线长为3,则该圆台的高为
【答案】
【详解】根据题意,作出圆台的图形,如图所示:
圆台上下底面的半径分别为1和2,母线长为3,
则圆台的高.
故答案为:.
知识点04 球的结构特征
(1)定义:半圆以它的直径所在直线为旋转轴,旋转一周形成的曲面叫做球面,球面所围成的旋转体叫做
球体,简称球
(2)相关概念:
球心:半圆的圆心
半径:连接球心和球面上任意一点的线段
直径:连接球面上两点并经过球心的线段
【即学即练4】(2024·全国·高一假期作业)铜钱又称方孔钱,是古代钱币最常见的一种.如图所示为清朝时的一枚“嘉庆通宝”,由一个圆和一个正方形组成,若绕旋转轴(虚线)旋转一周,形成的几何体是( )
A.一个球
B.一个球挖去一个圆柱
C.一个圆柱
D.一个球挖去一个正方体
【答案】B
【详解】圆及其内部旋转一周后所得几何体为球,
而矩形及其内部绕一边旋转后所得几何体为圆柱,
故题设中的平面图形绕旋转轴(虚线)旋转一周,形成的几何体为一个球挖去一个圆柱,
故选:B.
题型01 圆柱的结构特征
【典例1】(2023上·上海普陀·高二上海市宜川中学校考期中)我国古代数学名著《数书九章》中的一个问题,其意思为“圆木长2丈4尺,圆周长为一丈,葛藤从圆木的底部开始向上生长,绕圆木两周,刚好顶部与圆木平齐,问葛藤最少长几丈几尺.”(古制1丈=10尺)葛藤最少长是 .
【典例2】(2023·上海·高三专题练习)在圆柱中,底面圆半径为,高为,上底面圆的直径为,是底面圆弧上的一个动点,绕着底面圆周转,则的面积的范围 .
【变式1】(2023·高一课时练习)已知圆柱的母线长为l,底面半径为r,O是上底面圆心,是下底面圆周上两个不同的点,是母线.若直线与所成角的大小为,则 .
【变式2】(2023下·全国·高一专题练习)轴截面为正方形的圆柱叫做等边圆柱,已知某等边圆柱的轴截面面积为,求该等边圆柱的底面周长和高.
题型02 圆柱截面有关计算
【典例1】(2023上·辽宁·高二校联考阶段练习)如图,某圆柱的轴截面ABCD是边长为2的正方形,P,Q分别为线段BC,AC上的两个动点,E为上一点,且,则的最小值为( )
A.3B.C.D.
【典例2】(2023下·全国·高一专题练习)一个圆锥的底面半径为2,高为6,在其中有一个高为x的内接圆柱.
(1)用x表示圆柱的轴截面面积S;
(2)当x为何值时,S最大?
【变式1】(2022·全国·模拟预测)如图,圆柱的底面半径为2,四边形ABCD是圆柱的轴截面,点E在圆柱的下底面圆上,若圆柱的侧面积为,且,则( )
A.B.4C.D.
.
【变式2】(2023上·上海浦东新·高二校考期末)从一张半径为3的圆形铁皮中裁剪出一块扇形铁皮(如图1阴影部分),并卷成一个深度为米的圆锥筒(如图2).若所裁剪的扇形铁皮的圆心角为.
(1)求圆锥筒的容积;
(2)在(1)中的圆锥内有一个底面圆半径为的内接圆柱(如图3),求内接圆柱侧面积最大时的值.
题型03 圆柱展开图及最短距离问题
【典例1】(2024·全国·高三专题练习)如图,一个矩形边长为1和4,绕它的长为的边旋转二周后所得如图的一开口容器(下表面密封),是中点,现有一只妈蚁位于外壁处,内壁处有一米粒,若这只蚂蚁要先爬到上口边沿再爬到点处取得米粒,则它所需经过的最短路程为( )
A.B.C.D.
【典例2】(2023下·辽宁·高一校联考期末)如图,在圆柱中,,分别为圆,的直径,,,为的中点,则一只蚂蚁在圆柱表面从爬到的最短路径的长度为( )
A.B.C.D.
【典例3】(2024·全国·高一假期作业)如图,已知圆柱的高为h,底面半径为,轴截面为矩形,在母线上有一点,且,在母线上取一点,使,则圆柱侧面上P、Q两点的最短距离为 .
【变式1】(2024·广东·高三学业考试)如图在一根长11,外圆周长6的圆柱形柱体外表面,用一根细铁丝缠绕,组成10个螺旋,如果铁丝的两端恰好落在圆柱的同一条母线上,则铁丝长度的最小值为( )
A.61B.C.D.
【变式2】(2023·全国·高一专题练习)边长为5 cm的正方形EFGH是圆柱的轴截面,则从E点沿圆柱的侧面到相对顶点G的最短距离是( )
A.10cmB.5cm
C.5cmD.cm
【变式3】(2023·全国·高一专题练习)如图所示,圆柱高为2,底面半径为1,则在圆柱侧面上从A出发经过母线到达的最短距离为 .
题型04圆锥的结构特征
【典例1】(2024上·黑龙江牡丹江·高三牡丹江市第二高级中学校联考期末)已知圆锥的底面半径为4,其侧面展开图为一个四分之一圆,则该圆锥的母线长为( )
A.12B.14C.16D.18
【典例2】(2023·全国·高一专题练习)圆锥的轴截面有多少个?母线有多少条?圆锥顶点和底面圆周上任意一点的连线都是母线吗?
【变式1】(2023上·四川乐山·高二统考期末)如图,直角三角形绕直角边旋转,所得的旋转体为( )
A.圆锥B.圆柱C.圆台D.球
【变式2】(2023上·上海·高二专题练习)已知圆锥的轴截面是正三角形,它的面积是,则圆锥的高为 ;母线的长为 .
题型05 圆锥截面有关计算
【典例1】(2024·河南·模拟预测)已知圆锥侧面展开图是圆心角为直角,半径为2的扇形,则此圆锥内切球的半径为( )
A.B.C.D.
【典例2】(2023·山西阳泉·阳泉市第一中学校校考模拟预测)圆锥的母线长为4,侧面积是底面积的倍,过圆锥的两条母线作圆锥的截面,则该截面面积的最大值是( )
A.8B.C.D.
【典例3】(2023上·重庆·高二校联考开学考试)已知圆锥的底面面积为,高,则该圆锥的母线长为
【变式1】(2024·全国·高三专题练习)已知圆锥的母线长为2,其侧面展开图的中心角为,则过圆锥顶点的截面面积最大值为( )
A.1B.C.2D.
【变式2】(2024·广东惠州·统考一模)某圆锥的侧面展开图是面积为,圆心角为的扇形,则该圆锥的轴截面的面积是 .
【变式3】(2023上·全国·高三专题练习)在半径为的圆形广场中央上空,设置一个照明光源,射向地面的光呈圆锥形,且其轴截面顶角为.若要光源恰好照亮整个广场,则其高度应为 (精确到).
题型06 圆锥展开图及最短距离问题
【典例1】(2023下·山东泰安·高一泰安一中校考期中)某景区为提升游客观赏体验,搭建一批圆锥形屋顶的小屋(如图1).现测量其中一个屋顶,得到圆锥的底面直径长为,母线长为(如图2).若是母线的一个三等分点(靠近点S),从点A到点绕屋顶侧面一周安装灯光带,则灯光带的最小长度为( )
A.B.C.D.
【典例2】(2024·全国·高三专题练习)如图,在水平地面上的圆锥形物体的母线长为12,底面圆的半径等于4,一只小虫从圆锥的底面圆上的点P出发,绕圆锥侧面爬行一周后回到点处,则小虫爬行的最短路程为( )
A.B.16C.24D.
【典例3】(2023·上海宝山·统考一模)如图,在圆锥中,为底面圆的直径, ,点在底面圆周上,且.若为线段上的动点,则的周长最小值为
【变式1】(2024·全国·高一假期作业)如图,圆锥的底面圆直径AB为2,母线长SA为4,若小虫P从点A开始绕着圆锥表面爬行一圈到SA的中点C,则小虫爬行的最短距离为( )
A.B.C.D.
【变式2】(2023上·广东佛山·高三佛山一中校考阶段练习)如图,一个立在水平地面上的圆锥形物体的母线长为2,一只小虫从圆锥的底面圆上的点P出发,绕圆锥表面爬行一周后回到点P处,若该小虫爬行的最短路程为,则圆锥底面圆的半径等于 .
【变式3】(2023上·上海浦东新·高二上海市进才中学校考期中)如图是一座山的示意图,山呈圆锥形,圆锥的底面半径为10公里,母线长为40公里,母线一点,且公里,为了发展旅游业,要建设一条最短的从绕山一周到的观光铁路,则这段铁路的长度为 公里.
题型07 圆台的结构特征
【典例1】(2023下·陕西榆林·高一校考期中)下列给出的图形中,绕给出的轴旋转一周,能形成圆台的是( )
A. B. C. D.
【典例2】(2023·上海金山·统考一模)设圆台的上底面和下底面的半径分别为和,母线长为,则该该圆台的高为 .
【变式1】(2023下·全国·高一随堂练习)如图所示,用一个平行于圆锥底面的平面截这个圆锥,截得圆台上、下底面的面积之比为,截得圆台的圆锥的母线长为,求圆台的母线长.
【变式2】(2023·全国·高一随堂练习)—个圆台的母线长为5,两底面直径分别为2和8,求圆台的高.
题型08圆台展开图
【典例1】(2023下·山东潍坊·高一统考期末)如图,圆台的侧面展开图扇环的圆心角为,其中,则该圆台的高为( )
A.1B.C.D.4
【典例2】(2023·江苏·高一专题练习)如图所示,圆台的上底面半径为2,下底面半径为4,母线长为6.求轴截面相对顶点A、C在圆台侧面上的最短距离.
【变式1】(2023下·全国·高一专题练习)如图所示,圆台母线长为,上、下底面半径分别为和,从母线的中点M拉条绳子绕圆台侧面转到B点,求这条绳长的最小值.
【变式2】(2023下·高一课时练习)如图,圆台上、下底面半径分别为,,母线长为,从母线AB的中点拉一条细绳,围绕圆台侧面转至下底面的点,求BM间细绳的最短长度.
题型09 球的结构特征
【典例1】(2023上·四川乐山·高二统考期末)一个几何体,它的轴截面一定是圆面,则这个几何体是( )
A.圆柱B.圆锥C.圆台D.球
【典例2】(2023下·四川成都·高一树德中学校考阶段练习)半径为1的球放在教室的墙角,紧靠两墙面和地面,墙角顶点到球面上的点的最远距离是( )
A.2B.C.D.
【变式1】(2023下·山东枣庄·高一校考阶段练习)下列几何体是旋转体的是( )
A.五棱柱B.六棱锥C.八棱台D.球
【变式2】(2024上·全国·高三专题练习)东方明珠广播电视塔是上海的标志性文化景观之一,塔高约468米,上球体的直径为45米,且上球体的球心O到塔底的距离与塔高的比值为黄金分割比(约为0.618).若P为上球体球面上一点,且与地平面(塔顶与O的连线垂直地平面)所成的角为,P在上球体的上半部分,则P到地平面的距离约为( )
A.297米B.300米C.303米D.306米
题型10 球的截面性质及计算
【典例1】(2024上·安徽合肥·高三合肥市第八中学校联考期末)已知某圆台的上底面圆心为,半径为,下底面圆心为,半径为,高为,若该圆台的外接球球心为,且,则( )
A.B.C.D.
【典例2】(2023下·上海杨浦·高二统考期末)如图,已知球的半径为5,球心到平面的距离为3,则平面截球所得的小圆的半径长是( )
A.2B.3C.D.4
【典例3】(2024·全国·高三专题练习)毛泽东在《七律二首•送瘟神》中有句诗为“坐地日行八万里,巡天遥看一千河.”前半句的意思是:人坐在地面上不动,由于地球的自转,每昼夜会随着地面经过八万里路程.诗中所提到的八万里,指的是人坐在赤道附近所得到的数据.设某地所在纬度为北纬(即地球球心和该地的连线与赤道平面所成的角为),且.若将地球近似看作球体,则某人在该地每昼夜随着地球自转而经过的路程约为 万里.
【变式1】(2023上·北京·高二清华附中校考期中)已知平面与平面间的距离为3,定点,设集合,则S表示的曲线的长度为( )
A.B.C.D.
【变式2】(2023下·北京东城·高一北京二中校考阶段练习)经纬度是经度与纬度的合称,它们组成一个坐标系统,称为地理坐标系统,它是利用三维空间的球面来定义地球上的空间的球面坐标系.能够标示地球上任何一个位置,其中纬度是地球重力方向上的铅垂线与赤道平面所成的线面角.如世界最高峰珠穆朗玛峰就处在北纬30°,若将地球看成近似球体,其半径约为,则北纬30°纬线的长为( )
A.B.C.D.
【变式3】(2023上·上海·高二专题练习)已知球的半径为10 ,若它的一个截面圆的面积为,求球心与截面圆圆心的距离().
题型11 球面距
【典例1】(2023下·高一课时练习)如图,设地球的半径为,在北纬圈上有两个点、.在西经,在东经,则、两点间的球面距离为( )
A.B.C.D.
【典例2】(2023·全国·高三专题练习)已知A,B,C三点在球心为O,半径为R的球面上,,且,那么A,B两点的球面距离为 ,球心到平面的距离为 .
【变式1】(2023·全国·高一专题练习)球面上两点之间的最短连线的长度,就是经过这两个点的大圆在这两点间的一段劣弧的长度(大圆就是经过球心的平面截球面所得的圆),我们把这个弧长叫做两点的球面距离.已知正的顶点都在半径为的球面上,球心到所在平面距离为,则、两点间的球面距离为( )
A.B.C.D.
【变式2】(2023·上海浦东新·校考一模)在的二面角内放置一个半径为6的小球,它与二面角的两个半平面相切于、两点,则这两个点在球面上的距离是
题型12 简单组合体
【典例1】(2024·全国·高一假期作业)如图所示的几何体是数学奥林匹克能赛的奖杯,该几何体由( )
A.一个球、一个四棱柱、一个圆台构成
B.一个球、一个长方体、一个棱台构成
C.一个球、一个四棱台、一个圆台构成
D.一个球、一个五棱柱、一个校台构成
【典例2】(2024·全国·高一假期作业)若正五边形的中心为,以所在的直线为轴,其余五边旋转半周形成的面围成一个几何体,则( )
A.该几何体为圆台
B.该几何体是由圆台和圆锥组合而成的简单组合体
C.该几何体为圆柱
D.该几何体是由圆柱和圆锥组合而成的简单组合体
【典例3】(2024上·贵州·高三统考开学考试)已知“水滴”的表面是一个由圆锥的侧面和部分球面(常称为“球冠”)所围成的几何体.如图所示,将“水滴”的轴截面看成由线段AB,AC和优弧BC所围成的平面图形,其中点B,C所在直线与水平面平行,AB和AC与圆弧相切.已知“水滴”的“竖直高度”与“水平宽度”(“水平宽度”指的是平行于水平面的直线截轴截面所得线段的长度的最大值)的比值为,则( )
A.B.C.D.
【变式1】(2024·全国·高一假期作业)如图所示的简单组合体的组成是( )
A.棱柱、棱台B.棱柱、棱锥
C.棱锥、棱台D.棱柱、棱柱
【变式2】(2024上·河南漯河·高三漯河高中校考阶段练习)设为多面体的一个顶点,定义多面体在处的离散曲率为其中,为多面体的所有与点相邻的顶点,且平面,,…,,遍历多面体的所有以为公共点的面,如图是正四面体、正八面体、正十二面体和正二十面体(每个面都是全等的正多边形的多面体是正多面体),若它们在各顶点处的离散曲率分别是a,b,c,d,则a,b,c,d的大小关系是( )
A.B.
C.D.
【变式3】(2024·全国·高一假期作业)如图所示的几何体,关于其结构特征,下列说法不正确的是 .
①该几何体是由两个同底的四棱锥组成的几何体;
②该几何体有12条棱、6个顶点;
③该几何体有8个面,并且各面均为三角形;
④该几何体有9个面,其中一个面是四边形,其余均为三角形.
A夯实基础 B能力提升
A夯实基础
一、单选题
1.(2023·高三课时练习)如图,圆柱的高为2,底面周长为16,四边形ACDE为该圆柱的轴截面,点B为半圆弧CD的中点,则在此圆柱的侧面上,从A到B的路径中,最短路径的长度为( ).
A.B.C.3D.2
2.(2023上·湖北·高二宜昌市一中校联考阶段练习)已知圆锥侧面展开图是一个半圆,其母线长度为2,则底面半径为( )
A.1B.2C.3D.4
3.(2023下·天津西青·高一天津市西青区杨柳青第一中学校考期中)下列说法正确的是( )
A.有一个面是多边形,其余各面都是三角形的几何体叫做棱锥
B.用一个平面去截棱锥,底面和截面之间的部分叫做棱台
C.棱柱的侧面都是平行四边形
D.直角三角形绕一条边所在直线旋转一周得到的旋转体是圆锥
4.(2023上·上海奉贤·高二校联考期中)下列命题正确的是( )
A.以直角三角形的一直角边为轴旋转所形成的旋转体是圆锥
B.以直角梯形的一腰为轴旋转所形成的旋转体是圆台
C.圆柱、圆锥、圆台都有两个底面
D.圆锥的侧面展开图为扇形,这个扇形所在圆的半径等于圆锥底面圆的半径
5.(2023下·甘肃酒泉·高二校考期末)以下说法正确的是( )
A.半圆弧以其直径所在的的直线为轴旋转所成的曲面叫球;
B.球的大圆的半径等于球的半径;
C.球面和球是同一个概念;
D.经过球面上不同的两点只能做一个最大的圆.
6.(2023·高一课前预习)如图是由哪个平面图形旋转得到的( )
A. B.
C. D.
7.(2023·全国·高一专题练习)如图所示的螺母可以看成一个组合体,对其结构特征最接近的表述是( )
A.一个六棱柱中挖去一个棱柱B.一个六棱柱中挖去一个棱锥
C.一个六棱柱中挖去一个圆柱D.一个六棱柱中挖去一个圆台
8.(2023·全国·高一专题练习)如图,圆柱的轴截面ABCD是一个边长为4的正方形.一只蚂蚁从点A出发绕圆柱表面爬到BC的中点E,则蚂蚁爬行的最短距离为( )
A.B.C.D.
9.(2023上·辽宁沈阳·高二沈阳市第一二〇中学校考阶段练习)古希腊著名数学家欧几里德在《几何原本》一书中定义了圆锥与直角圆锥这两个概念:固定直角三角形的一条直角边,旋转直角三角形到开始位置,所形成的图形称为圆锥;如果固定的直角边等于另一直角边时,所形成的圆锥称为直角圆锥,则直角圆锥的侧面展开图(为一扇形)的圆心角的大小为( )
A.B.
C.D.与直角圆锥的母线长有关
10.(2023·山西朔州·怀仁市第一中学校校考模拟预测)毛泽东在《七律二首•送瘟神》中有句诗为“坐地日行八万里,巡天遥看一千河.”前半句的意思是:人坐在地面上不动,由于地球的自转,每昼夜会随着地面经过八万里路程.诗中所提到的八万里,指的是人坐在赤道附近所得到的数据.设某地所在纬度为北纬(即地球球心和该地的连线与赤道平面所成的角为),且.若将地球近似看作球体,则某人在该地每昼夜随着地球自转而经过的路程约为( )
A.万里B.万里C.万里D.万里
二、多选题
11.(2023下·广东深圳·高一深圳市建文外国语学校校考期中)用一张长为8,宽为4的矩形硬纸卷成圆柱的侧面,则相应圆柱的底面半径可能是
A.B.C.D.
12.(2023·全国·高三专题练习)已知圆锥底面半径为,母线长为2,则( )
A.圆锥侧面积为
B.圆锥的侧面展开图中,扇形的圆心角为
C.圆锥的体积为
D.过顶点的截面三角形的面积最大值为
三、填空题
13.(2023上·上海浦东新·高二校考期中)若圆锥的侧面展开图是半径为,面积为的扇形,则由它的两条母线所确定的该圆锥的截面面积的最大值为 .
14.(2023下·浙江台州·高一校联考期中)已知圆柱体的底面半径为,高为,一只蜗牛从圆柱体底部开始爬行,绕圆柱体4圈到达顶部,则蜗牛爬行的最短路径长为 .
15.(2023上·陕西榆林·高三榆林市第一中学校联考阶段练习)已知某圆台的上底面圆心为,半径为r,下底面圆心为,半径为2r,高为h.若该圆台的外接球球心为O,且,则 .
四、解答题
16.(2023上·高二课时练习)如图所示,已知圆柱的高为80cm,底面半径为10cm,表面上有P、Q两点,若P点在B点处、Q点在点处,一只蚂蚁沿着侧面从P点爬到Q点(不直接走直线段),求蚂蚁爬行的最短路程.
17.(2023下·全国·高一专题练习)已知圆锥的底面半径为3,沿该圆锥的母线把侧面展开后可得到圆心角为π的扇形.
(1)求该圆锥的高;
(2)求圆锥的母线与底面所成角的大小.
18.(2023·全国·高一随堂练习)请解决下列问题:
(1)已知一个圆台的轴截面是下底为且其余边长为的等腰梯形,求圆台的高;
(2)用一个平行于圆锥底面的平面截这个圆锥,截得圆台上、下底面半径的比是,截去的圆锥的母线长是,求圆台的母线长.
B能力提升
1.(2023下·高一课时练习)如图,已知圆柱体底面圆的半径为,高为2cm,AB,CD分别是两底面的直径,AD,BC是母线.若一只小虫从点A出发,沿侧面爬行到点C处,则小虫爬行的最短距离是( )
A.B.2cmC.D.1cm
2.(2023下·河南驻马店·高三统考阶段练习)已知底面边长为1的正三棱柱既有外接球也有内切球,圆锥是三棱柱的外接圆锥,且三棱柱的一个底面在该圆锥的底面上,则该外接圆锥的轴截面面积的最小值是( )
A.B.C.D.
3.(2023上·山西大同·高三统考期末)已知圆台的上、下底面的圆心分别为,,母线(点位于上底面),且,圆的周长为,一只蚂蚁从点A出发沿着圆台侧面爬行一周到点B,则其爬行的最短路程为( )
A.1B.C.2D.
4.(2023上·上海·高二专题练习)已知圆柱的底面圆半径为1,高为2,为上底面圆的一条直径,是下底面圆周上的一个动点,则△的面积的取值范围为
5.(2023·安徽铜陵·统考三模)如图是一座山的示意图,山大致呈圆锥形,山脚呈圆形,半径为2km,山高为,是山坡上一点,且.现要建设一条从到的环山观光公路,这条公路从出发后先上坡,后下坡,当公路长度最短时,下坡路段长为 .
课程标准
学习目标
①了解圆柱、圆锥、圆台、球的定义.2.掌握圆柱、圆锥、圆台、球的结构特征。
②了解简单组合体的概念及结构特征。
③了解简单组合体的概念及结构特征
1.通过阅读课本解圆柱、圆锥、圆台、球的定义;
2.在棱柱、棱锥与棱台学习的基础上,进一步掌握圆柱、圆锥、圆台、球的结构特征;
3.了解简单组合体的概念及结构特征.灵活运用各种知识解决组合体问题;
高中数学人教A版 (2019)必修 第二册8.1 基本立体图形优秀第2课时巩固练习: 这是一份高中数学人教A版 (2019)必修 第二册8.1 基本立体图形优秀第2课时巩固练习,共8页。试卷主要包含了关于下列几何体,说法正确的是,下列关于球体的说法中,错误的是,解析等内容,欢迎下载使用。
数学人教A版 (2019)8.1 基本立体图形第2课时课后练习题: 这是一份数学人教A版 (2019)8.1 基本立体图形第2课时课后练习题,共8页。试卷主要包含了1 基本立体图形,下列几何体中不是旋转体的是,下列说法错误的是等内容,欢迎下载使用。
人教A版 (2019)必修 第二册8.1 基本立体图形课时作业: 这是一份人教A版 (2019)必修 第二册8.1 基本立体图形课时作业,共4页。













