北师大版数学七年级下册 第二章 《相交线与平行线》单元小结 课件+单元测试（含答案解析）

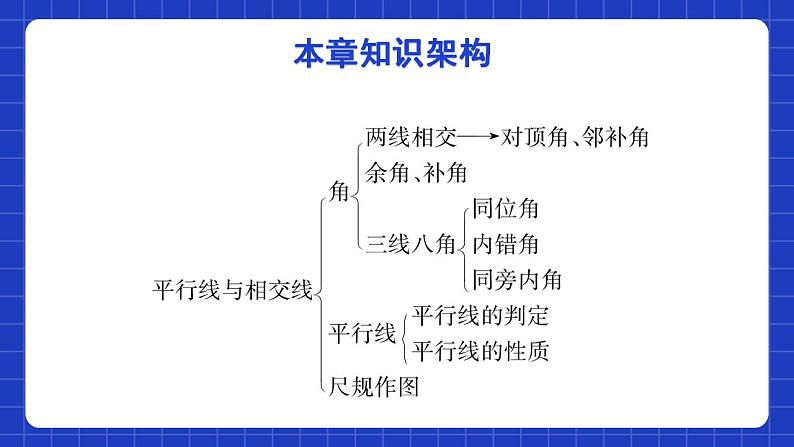
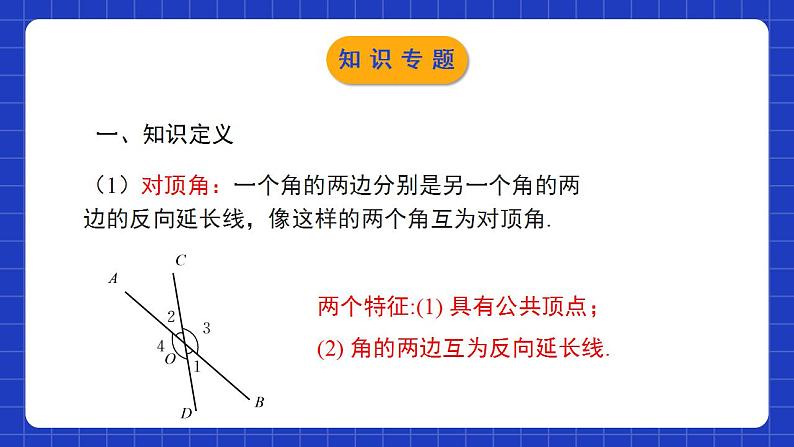
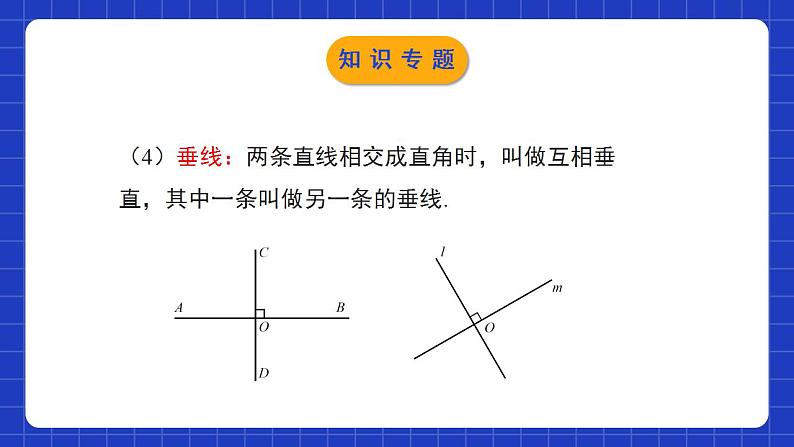
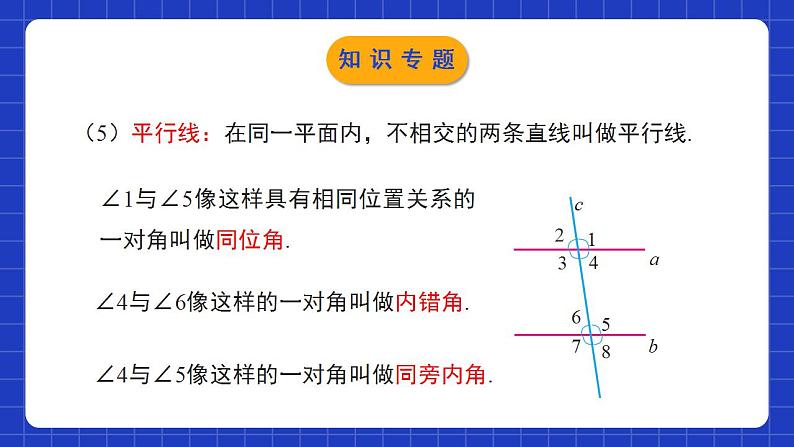
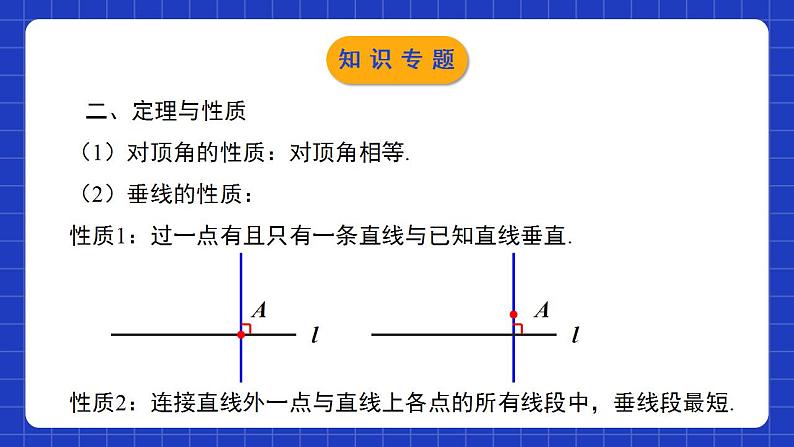
第二章 相交线与平行线单元小结本章知识架构一、知识定义（1）对顶角：一个角的两边分别是另一个角的两边的反向延长线，像这样的两个角互为对顶角.两个特征:(1) 具有公共顶点；(2) 角的两边互为反向延长线.知识专题（2）补角：如果两个角的和是180°，那么称这两个角互为补角.（3）余角：如果两个角的和是90°，那么称这两个角互为余角.知识专题（4）垂线：两条直线相交成直角时，叫做互相垂直，其中一条叫做另一条的垂线.知识专题（5）平行线：在同一平面内，不相交的两条直线叫做平行线.∠1与∠5像这样具有相同位置关系的一对角叫做同位角.∠4与∠6像这样的一对角叫做内错角.∠4与∠5像这样的一对角叫做同旁内角.知识专题二、定理与性质（1）对顶角的性质：对顶角相等.（2）垂线的性质：性质1：过一点有且只有一条直线与已知直线垂直.性质2：连接直线外一点与直线上各点的所有线段中，垂线段最短.知识专题（3）平行公理：经过直线外一点有且只有一条直线与已知直线平行.（4）平行公理的推论：如果两条直线都与第三条直线平行，那么这两条直线也互相平行.知识专题（5）平行线的性质：性质1：两直线平行，同位角相等.性质2：两直线平行，内错角相等.性质3：两直线平行，同旁内角互补.知识专题（6）平行线的判定：判定1：同位角相等，两直线平行.判定2：内错角相等，两直线平行.判定3：同旁内角互补，两直线平行.三、尺规作图知识专题考点一： 两条直线相交构成的角的相关计算例1：如图, 直线AB与直线CD相交于点O, 已知OE⊥AB于点O, ∠BOD=45°, 则∠COE的度数是( ).A．125° B．135°C．145° D．155°B考点专练考点专练【要点指导】两条直线相交形成四个角, 这四个角中有两对对顶角、四对邻补角；当相交的两条直线互相垂直时, 相交形成的角是直角. 根据对顶角、邻补角之间的数量关系以及直角的定义, 可进行角度的相关计算.考点专练考点二：关于两点之间、点与直线之间的距离例2： 如图所示, AB∥CD, DE⊥AB于点E, 经测量知AD=BC=1.6 cm, DE=1.4 cm.(1)BC的长表示什么之间的距离？(2)点D到直线AB的距离是1.4 cm还是1.6 cm？为什么？考点专练解： (1)BC的长表示点B与点C之间的距离.(2)点D到直线AB的距离是1.4 cm. 理由：因为DE⊥AB , 所以DE是点D到直线AB的垂线段, 所以点D到直线AB的距离是1.4 cm.考点专练【要点指导】直线外一点到这条直线的垂线段的长度叫作点到直线的距离, 这说明, 点到直线的距离可以转化为两点之间的距离.考点专练考点三：与平行线性质、判定有关的计算与说理题 例3：已知：如图, AB∥CD, BD平分∠ABC, CE平分∠DCF, ∠ACE=90°.(1)判断BD和CE的位置关系, 并说明理由；(2)判断AC和BD是否垂直, 并说明理由．考点专练考点专练考点专练【要点指导】综合利用题目中角的数量关系判定两直线平行, 再根据平行线的性质得出另外一对相等或互补的角, 从而进行相关的计算或说理；或先通过平行线得出角的相等或互补关系, 再根据平行线的判定得出另一组直线互相平行.考点专练考点四：平行与垂直的综合运用例4：如图, 已知AD⊥BC于点D, EG⊥BC于点G, ∠E=∠1, AD平分∠BAC吗？试说明理由．考点专练考点专练考点专练【要点指导】垂直是特殊的相交, 在数学图形中, 平行和垂直经常同时出现, 解决问题时既要注意从线角关系的角度转化问题、推导出结论, 还要注意从线线关系的角度发现结论、转化问题, 多角度思考问题.考点专练课程结束