初中8 圆内接正多边形完美版课件ppt

这是一份初中8 圆内接正多边形完美版课件ppt，共24页。PPT课件主要包含了学习目标，情境导入，正多边形与圆的关系，圆内接，正三角形的外接圆，正方形的外接圆，正五边形的外接圆，正三角形，正方形，正五边形等内容，欢迎下载使用。

能运用正多边形的知识解决圆的有关计算问题；
掌握正多边形和圆的关系；
理解正多边形的中心、半径、中心角、边心距等概念；
会运用多边形知和圆的有关知识画多边形.
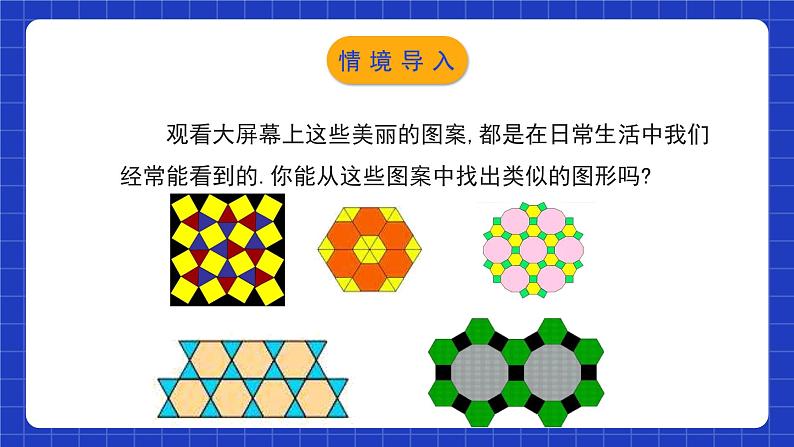
观看大屏幕上这些美丽的图案,都是在日常生活中我们经常能看到的.你能从这些图案中找出类似的图形吗?
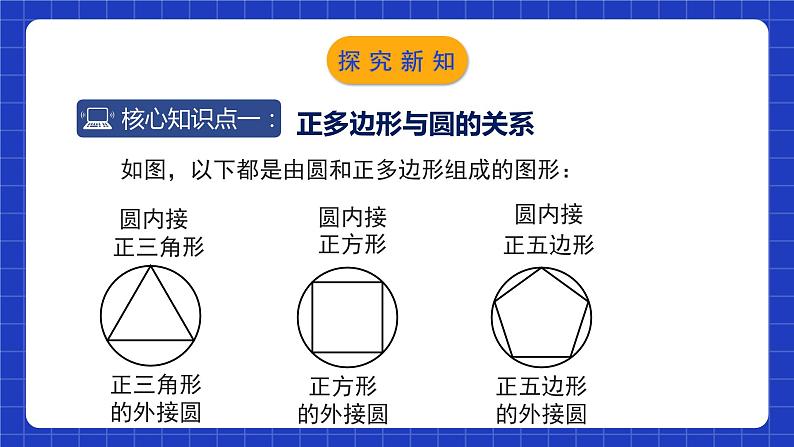
如图，以下都是由圆和正多边形组成的图形：
正多边形的顶点都在圆上
正多边形在圆的内部，圆在正多边形的外部
顶点都在同一圆上的正多边形叫做圆内接正多边形。
这个圆叫做该正多边形的外接圆。
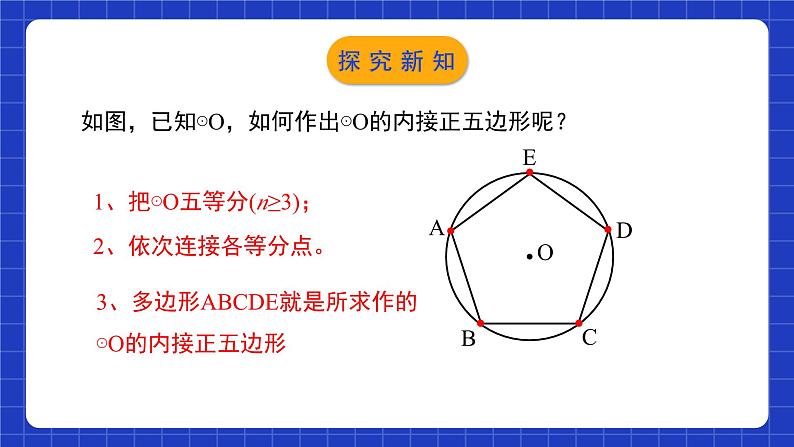
如图，已知⊙O，如何作出⊙O的内接正五边形呢？
1、把⊙O五等分(n≥3)；
2、依次连接各等分点。
3、多边形ABCDE就是所求作的 ⊙O的内接正五边形
把圆分成n（n≥3）等份：依次连接各分点所得的多边形是这个圆的内接正n边形；
圆内接正多边形的画法：
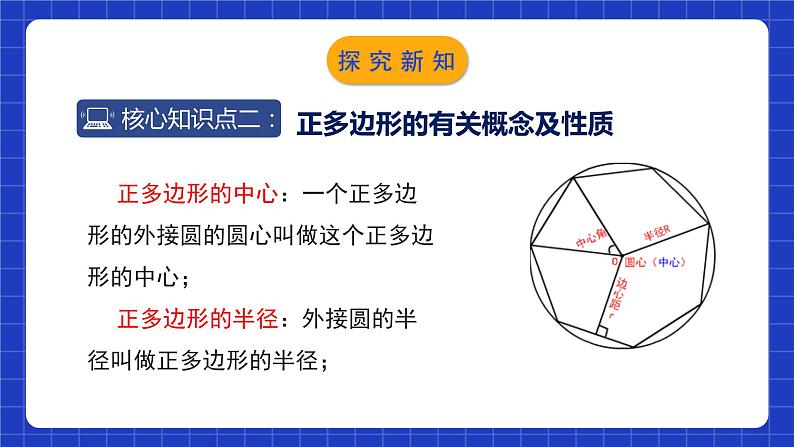
正多边形的有关概念及性质
正多边形的中心：一个正多边形的外接圆的圆心叫做这个正多边形的中心；正多边形的半径：外接圆的半径叫做正多边形的半径；
正多边形的中心角：正多边形每一边所对的圆心角叫做正多边形的中心角，正多边形的中心角都等于360°/n （n为正多边形的边数，n≥3），正多边形的边心距：中心到正多边形的一边的距离叫做正多边形的边心距.
（1）任意一个三角形都有一个外接圆和内切圆，但只有正三角形的外接圆和内切圆才是同心圆；（2）任意多边形不一定有外接圆和内切圆，但多边形是正多边形时一定有一个外接圆和内切圆，并且是同心圆。
圆内接正多边形的有关计算
1、正n边形的每个中心角等于 .
2、 正n边形的内角和等于 . 每个内角等于 .
3、正n边形的每个外角等于 . 正多边形的中心角与外角的大小关系是 .
4、正n边形的边长a，半径R，边心距r之间满足 .
5、边长a，边心距r的正n边形的面积为 。
例： 如图,在圆内接正六边形ABCDEF中，半径OC = 4, OG丄BC，垂足为G，求这个正六边形的中心角、边长和边心距.
解：连接OD.∵六边形ABCDEF为正六边形，∴ ∠ COD = = 60°∴ △COD为等边三角形.∴ CD = OC = 4.在 Rt △ COG中，OC = 4，CG= BC= ×4=2,∴ OG = ∴正六边形的中心角为60°，边长为4,边心距为
3．正多边形的中心角与该正多边形的一个内角的关系为(　　) A．两角互余 B．两角互补 C．两角互余或互补 D．不能确定
5.正n边形的一个内角与一个外角之比是5∶1，那么n等于 .6.若一正四边形与一正八边形的周长相等，则它们的边长之比为 .7.有两个正多边形边数比为2∶1，内角度数比为4∶3，它们的边数 .
8.如图，已知△ABC是⊙O的内接等腰三角形，顶角∠A=36°，弦BD、CE分别平分∠ABC、∠ACB，求证：五边形AEBCD是正五边形.
证明：∵△ABC是等腰三角形，且∠A=36°∴∠ABC=∠ACB=72°又∵BD平分∠ABC，CE平分∠ACB∴∠ABD=∠CBD=∠ACE=∠BCE=36°即∠BAC=∠ABD=∠CBD=∠ACE=∠BCE∴BC=AD=CD=AE=BE∴A、E、B、C、D是⊙O的五等分点∴五边形AEBCD是正五边形.
添加辅助线的方法：连半径，作边心距
正n边形各顶点等分其外接圆.