初中数学人教版七年级下册第五章 相交线与平行线5.2 平行线及其判定5.2.2 平行线的判定备课ppt课件

这是一份初中数学人教版七年级下册第五章 相交线与平行线5.2 平行线及其判定5.2.2 平行线的判定备课ppt课件，共21页。PPT课件主要包含了在同一平面内，教科书第12页，∴∠7∠3，∴AB∥CD，几何语言，角平分线的定义，对顶角相等，等量代换，∠330°，解AB∥CD等内容，欢迎下载使用。

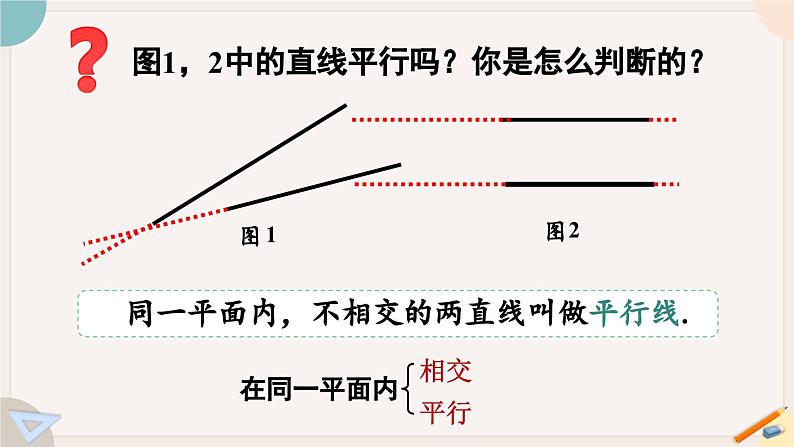
图1，2中的直线平行吗？你是怎么判断的？
我们已经学习过用三角尺和直尺画平行线的方法.
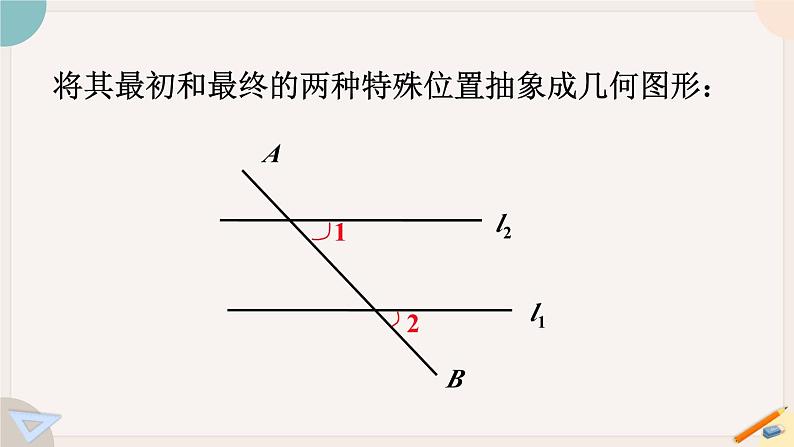
将其最初和最终的两种特殊位置抽象成几何图形：
判定方法1：两条直线被第三条直线所截，如果同 位角相等，那么这两条直线平行.
简单说成：同位角相等，两直线平行.
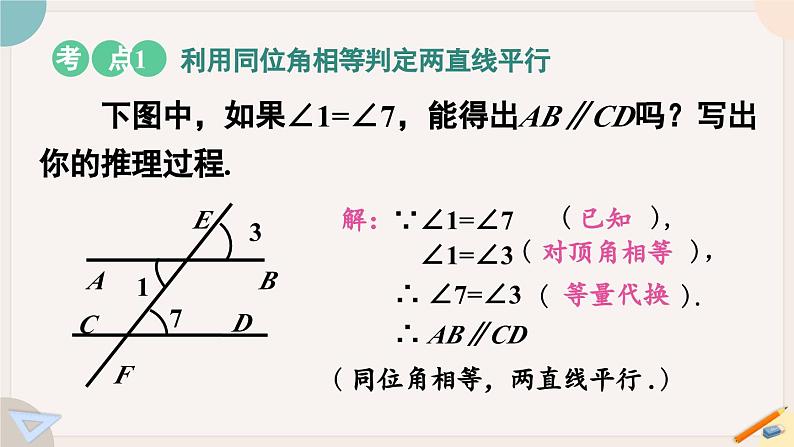
下图中，如果∠1=∠7，能得出AB∥CD吗？写出你的推理过程.
解：∵∠1=∠7 ∠1=∠3
利用同位角相等判定两直线平行
如图，由3=2，可推出a//b吗？如何推出？
解： ∵ 2=3(已知）， 3=1（对顶角相等）， ∴1=2. ∴ a//b(同位角相等，两直线平行）.
判定方法2：两条直线被第三条直线所截，如果内 错角相等，那么这两条直线平行.
简单说成：内错角相等，两直线平行.
∵ ∠3=∠2(已知),∴ a∥b(内错角相等，两直线平行).
完成下面证明：如图所示，CB平分∠ACD，∠1=∠3. 求证：AB∥CD. 证明：∵CB平分∠ACD，∴∠1=∠2( _______).∵∠1=∠3，∴∠2=∠ . ∴AB∥CD( _).
内错角相等，两直线平行
利用内错角相等判定两直线平行
如图，如果1+2=180° ，你能判定a//b吗?
解：能, ∵1+2=180°（已知）, 1+3=180°（邻补角的性质）,∴2=3（同角的补角相等） .∴a//b（同位角相等，两直线平行） .
判定方法3：两条直线被第三条直线所截，如果同旁 内角互补，那么这两条直线平行.
简单说成：同旁内角互补，两直线平行.
∵∠1+∠2=180°(已知),∴a∥b（同旁内角互补，两直线平行）.
如图：直线AB、CD都和AE相交，且∠1+∠A=180º . 求证：AB//CD .
证明：∵∠1+∠A=180º
∴∠2+∠A=180º
（ ）.
∠1=∠2 （ ）,
利用同旁内角互补判定两直线平行
1. 如图，可以确定AB∥CE的条件是( ) A.∠2=∠B B. ∠1=∠A C. ∠3=∠B D. ∠3=∠A
2. 如图，已知 ∠1 = 30°，若∠3 满足条件 ____________________，则 a∥b.
① ∵ ∠1 =_____（已知）, ∴ AB∥CE( );
② ∵ ∠1 +_____=180（已知）, ∴CD∥BF( );
内错角相等,两直线平行
同旁内角互补,两直线平行
3. 根据条件完成填空:
③ ∵ ∠1 +∠5 =180（已知）, ∴ ___∥_____( );
④ ∵ ∠4 +_____=180（已知）, ∴ CE∥AB( ).
理由如下： ∵ AC平分∠DAB（已知）, ∴ ∠1=∠2（角平分线定义）. 又∵ ∠1= ∠3（已知） , ∴ ∠2=∠3（等量代换）. ∴ AB∥CD(内错角相等，两直线平行).
4. 如图，已知∠1= ∠3，AC平分∠DAB，你能判断哪 两条直线平行？请说明理由？
1.从课后习题中选取；2.完成练习册本课时的习题。