




初中人教版14.1.2 幂的乘方多媒体教学ppt课件
展开五彩缤纷的世界物质由分子与原子组成,原子核(atmic nucleus)位于原子的核心部分,占了99.96%以上原子的质量,与周围围绕的电子组成原子。原子核由质子和中子构成。其中分子的直径一般为10-10m,电子的直径一般为10-16m,如果把分子和电子均看作球体,已知球的体积公式为V球 = πr3,其中 V 是球的体积,r 是球的半径.那么,分子的体积是电子的多少倍?
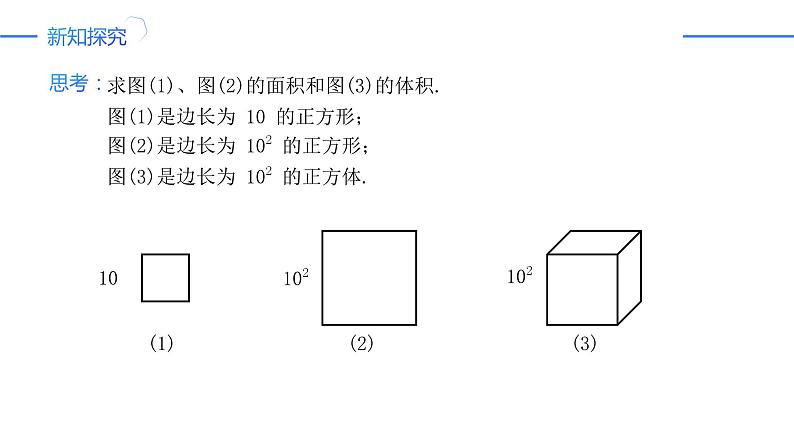
求图(1)、图(2)的面积和图(3)的体积.图(1)是边长为 10 的正方形;图(2)是边长为 102 的正方形;图(3)是边长为 102 的正方体.
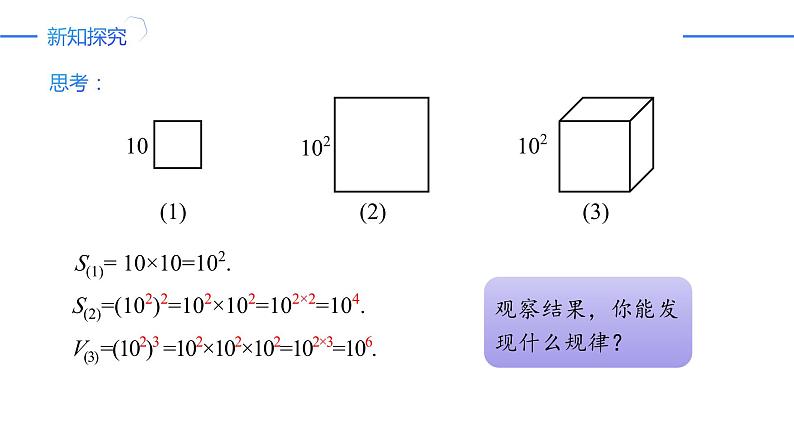
S(1)= 10×10=102.
S(2)=(102)2=102×102=102×2=104.
V(3) =(102)3 =102×102×102=102×3=106.
观察结果,你能发现什么规律?
请根据乘方的意义及同底数幂的乘法法则填空,观察计算的结果,你能发现什么规律?证明你的猜想.
(52)3 = ___ ×___ ×___ = 5( )+( )+( ) = 5( )×( ) = 5( ).
观察计算结果,你发现了什么规律?
(1)(52)35252525(222) 5( 6 );
(2)(a2)3a2·a2·a2a(222) a( 6 );
(3)(am)3am·am·ama(mmm) a( 3m )(m是正整数).
5( 23 );
a( 23 );
1.结果的底数与原来的底数相同;2.结果的指数等于原来两个指数的积.
a( 3·m )(m是正整数).
(am)n = amn (m,n 都是正整数).
即幂的乘方,底数______,指数____.
计算:(1) (103)3 ; (2) -(xm)5 ; (3) (a2)3·a5 ; (4) -[(a-b)7 ]2.
解:(1) (103)3=103×3=109 ;
(2) -(xm)5=-xm×5=-x5m ;
(3) (a2)3·a5=a2×3+5=a11 .
(4) -[(a-b)7 ]2 = -(a-b)7×2= -(a-b)14 .
运用幂的乘方法则进行计算时,一定不要将幂的乘方与同底数幂的乘法混淆,在幂的乘方中,底数可以是单项式,也可以是多项式.
与 的结果相同吗?
(-a7)2 表示 2 个 -a7 相乘,结果没有负号.
(-x2)7 表示 7 个 -x2 相乘,其结果带有负号.
[(y3)2]2=______=________
[(x7)m]n=______=________
(am)n =(an)m = amn (m,n 都是正整数).
(2) a2 (-a)2 (-a2)3+a10
(1) (x4)3 · x6;
(2) a2 (-a)2 (-a2)3+a10.
解:(1) (x4)3 · x6 = x12 · x6 = x18.
= -a2 · a2 · a6+a10
= -a10+a10 = 0.
与幂的乘方有关的混合运算中,一般先算幂的乘方,再算同底数幂的乘法,最后算加减,即合并同类项.
已知 a2n=3,求 a4n-a6n 的值.
解:a4n-a6n = (a2n)2- (a2n)3= 32-33=-18 .
分析:把指数是积的形式的幂写成幂的乘方,如, amn=(am)n(m,n都是正整数),然后整体代入,求出式子的值.
已知16m=4×22n-2,27n=9×3m+3 ,求 m,n 的值.
所以(24)m =22×22n-2 .
所以4m=2n,即2m=n. ①
所以(33)n=32×3m+3 .
所以3n=m+5. ②
比较 355,444 ,533 的大小.
解: 355 = (35)11 = 24311 , 444 = (44)11 = 25611 , 533 = (53)11 = 12511 . 因为125<243<256, 所以12511<24311<25611 . 即 533<355< 444 .
比较底数大于 1 的幂的大小的方法有两种:(1) 底数相同,指数越大,幂就越大;(2) 指数相同,底数越大,幂就越大. 故在此类题中,一般先观察题目所给数据的特点,将其转化为同底数或同指数的幂,然后再去比较大小.
(am)n = amn ( m,n 都是正整数)
幂的乘方,底数不变,指数相乘
幂的乘方与同底数幂的乘法的区别:(am)n = amn;am·an = am+n
幂的乘方法则的逆用:amn = (am)n = (an)m
1.若k为正整数,则(k+k+…+k)k=( )A. k2kB. k2k+1C. 2kkD. k2+k
2. 下列计算中,错误的是 ( )A.[(a+b)2]3=(a+b)6 B.[(a+b)2]5=(a+b)7C.[(a-b)3]n=(a-b)3n D.[(a-b)3]2=(a-b)6
(1) (x4)3·x6;
(2) a2(-a)2(-a2)3+a10.
解: (1) (x4)3·x6 =x12·x6= x18;
(2) a2(-a)2(-a2)3+a10
= -a2·a2·a6+a10
= -a10+a10 = 0.
(6) [(﹣x)4]3.
(5) [(x+y)2]3;
(3) (am)2 =am·2=a2m;
(4) -(x4)3 =-x4×3=-x12;
(5)[(x+y)2]3= (x+y)2×3 =(x+y)6;
(6)[(﹣x)4]3= (﹣x)4×3 = (﹣x)12 = x12.
4.已知 a2n=3,求 a4n-a6n 的值.
5.已知10m=3,10n=2,求下列各式的值. (1)103m;(2)102n;(3)103m+2n.
解:(1)103m=(10m)3=33=27;
(2)102n=(10n)2=22=4;
(3)103m+2n=103m×102n=27×4=108.
6.(1) 已知 x2n=3,求 (x3n)4 的值;
(2) 已知 2x+5y-3=0,求 4x · 32y 的值.
解:(1) (x3n)4=x12n=(x2n)6=36=729.
(2) ∵ 2x+5y-3=0, ∴ 2x+5y=3. ∴ 4x · 32y=(22)x · (25)y=22x · 25y=22x+5y=23=8.
初中数学人教版八年级上册第十四章 整式的乘法与因式分解14.1 整式的乘法14.1.2 幂的乘方课文课件ppt: 这是一份初中数学人教版八年级上册第十四章 整式的乘法与因式分解14.1 整式的乘法14.1.2 幂的乘方课文课件ppt,共17页。PPT课件主要包含了创设情境导入新知,细心观察归纳总结,幂的乘方性质,动脑思考例题解析,动脑思考变式训练,动手操作得出性质,归纳总结,归纳小结等内容,欢迎下载使用。
人教版八年级上册第十四章 整式的乘法与因式分解14.1 整式的乘法14.1.2 幂的乘方背景图课件ppt: 这是一份人教版八年级上册第十四章 整式的乘法与因式分解14.1 整式的乘法14.1.2 幂的乘方背景图课件ppt,共44页。PPT课件主要包含了乘方的意义,幂的乘方,同底数幂的乘法,加减合并同类项,研究过程等内容,欢迎下载使用。
数学14.1.2 幂的乘方教课ppt课件: 这是一份数学14.1.2 幂的乘方教课ppt课件,共17页。PPT课件主要包含了创设情境,我们知道,幂的乘方法则,幂的乘方公式,mn都是正整数,例1计算,注意符号的处理,例2计算,运算顺序该怎样,运算顺序等内容,欢迎下载使用。













