人教版七年级上册4.3.2 角的比较与运算课文ppt课件

这是一份人教版七年级上册4.3.2 角的比较与运算课文ppt课件，文件包含432角的比较与运算-人教版初中数学七年级上册pptx、情境引入mp4、折纸法作角平分线mp4等3份课件配套教学资源，其中PPT共42页， 欢迎下载使用。

1.掌握角的大小的比较方法. 2.理解角平分线和角的和、差、倍、分的意义及数量关系，能够用几何语言进行相关表述，并能解答相关问题. 3.会进行涉及度、分、秒的角度的计算.
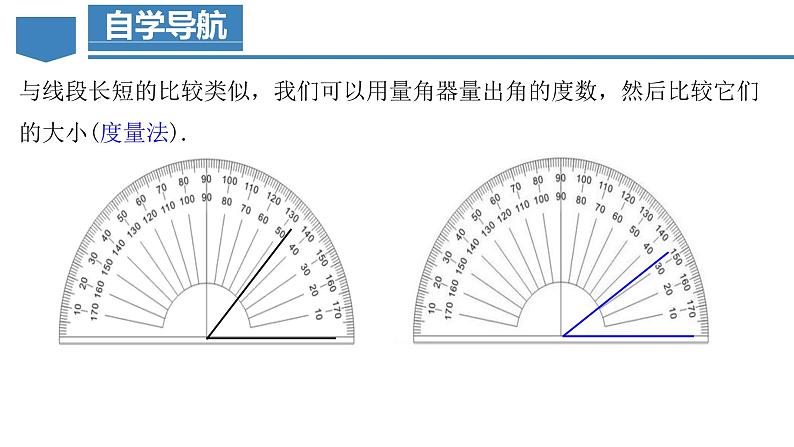
与线段长短的比较类似，我们可以用量角器量出角的度数，然后比较它们的大小(度量法).
也可以把它们的一条边叠合在一起，通过观察另一条边的位置来比较两个角的大小(叠合法)
∠AOB____∠A'O'B'
∠AOB ____∠A'O'B'
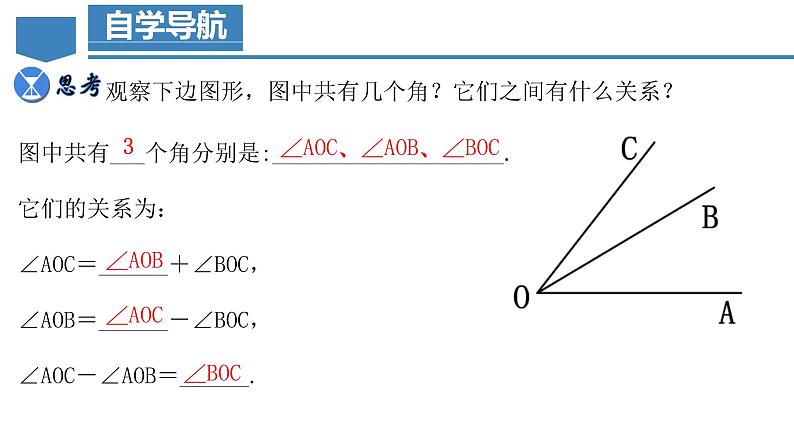
观察下边图形，图中共有几个角？它们之间有什么关系？
图中共有___个角分别是:____________________.它们的关系为：∠AOC＝______＋∠BOC，∠AOB＝______－∠BOC，∠AOC－∠AOB＝______.
∠AOC、∠AOB、∠BOC
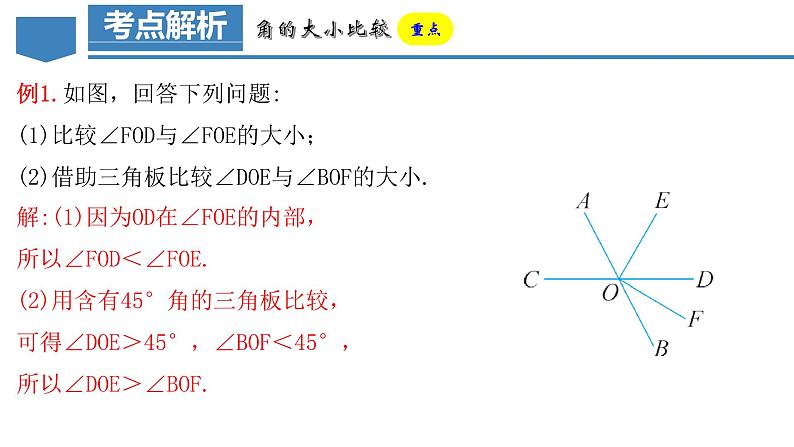
例1.如图，回答下列问题:(1)比较∠FOD与∠FOE的大小；(2)借助三角板比较∠DOE与∠BOF的大小.
解:(1)因为OD在∠FOE的内部，所以∠FOD＜∠FOE.(2)用含有45°角的三角板比较，可得∠DOE＞45°，∠BOF＜45°，所以∠DOE＞∠BOF.
1.在∠AOB的内部任取一点C，作射线OC，则一定存在( )A.∠AOB＞∠AOC B.∠AOC=∠BOC C.∠BOC＞∠AOC D.∠AOC＞∠BOC2.如图，∠AOF是平角，请你比较∠AOB，∠AOC，∠AOD，∠AOE四个角的大小.
解:观察图形即可判断四个角的大小，即∠AOB＜∠AOC＜∠AOD＜∠AOE.
例2.观察图形并回答下列问题:(1)∠AOC是哪两个角的和?∠DOB是哪两个角的和?(2)∠AOB是哪两个角的差?
解:(1)∠AOC是∠AOB与∠BOC的和，∠DOB是∠COD与∠BOC的和.即∠AOC=∠AOB+∠BOC，∠DOB=∠COD+∠BOC.(2)∠AOB是∠AOC与∠BOC的差，或∠AOB是∠AOD与∠DOB的差.即∠AOB=∠AOC-∠BOC=∠AOD-∠DOB.
1.按图填空:(1)∠AOB+∠BOC=________;(2)∠BOD-∠COD=________;(3)∠AOD=∠AOB+∠B0C+_______; =∠AOB+______; =∠AOC+______;(4)∠BOC=∠AOD-∠AOB-_______; =∠AOC-_______; =∠B0D-_______.
2.如图，∠AOB=∠COD，则( ) A.∠l＞∠2 B.∠1=∠2 C.∠1＜∠2 D.∠1与∠2的大小无法比较
如图，借助三角尺画出15°，75°的角，用一副三角尺，你还能画出哪些度数的角？试一试.
【结论】借助一副三角尺可以画出15°倍数的角.
我们知道，线段的中点把线段分成相等的两条线段.类似地，下图中，如果∠AOB＝∠BOC，那么射线OB把∠AOC分成两个相等的角，这时有
一般地，从一个角的顶点出发，把这个角分成两个相等的角的射线，叫做这个角的平分线.
OB是∠AOC的平分线
三等分线OB，OC是∠AOD的三等分线.
1.如图，O是直线AB上一点，OC是∠AOB的平分线，∠COD=32°，则∠BOD的度数是_______.2.如图，OC是∠AOB的平分线，OD是∠AOC的平分线，∠COD=25°，则∠AOB等于( )A.50° B.75° C.100° D.120°
3.如图，∠AOB=165°，0D平分∠AOC.(1)若∠AOD=50°，则∠B0C=_______.(2)若∠BOD=110°，则OC是∠BOD的平分线吗?说明理由.
解：(2)0C是∠BOD的平分线.理由:因为∠AOB=165°,∠BOD=110°，所以∠AOD=∠AOB-∠BOD=165°-110°=55°.因为0D平分∠AOC，所以∠COD=∠AOD=55°.所以∠BOC=∠BOD-∠COD=110°-55°=55°.所以∠BOC=∠COD.所以OC是∠BOD的平分线.
例4.计算:(1)56°18′+72°48′; (2)131°28′-51°32′15″;(3)12°30′20″×2; (4)12°31′21″÷3.
解:(1)56°18′+72°48′=128°66′=129°6′;(2)131°28′-51°32′15″=130°87′60″-51°32′15″=79°55′45″;
(3)12°30′20″×2= 24°60′40″= 25°40″;
(4)12°31′21″÷3=4°+31′21″÷3=4°10′+81″÷3=4°10′27″.
1.如图，O是直线AB上一点，OD是∠BOC的平分线，∠AOC=46°38′，则∠BOD的度数为________.
2.计算:(1)48°39′+67°31′-21°17′; (2)23°53′×3-107°43′÷5.
解:(1)48°39′+67°31′-21°17′= 116°10′-21°17′= 94°53′.
(2)23°53′×3- 107°43′÷5=71°39′-21°32′36″=50°6′24″.
利用已知条件直接求角度
例5.如图，已知∠AOB=90°，∠COD=90°，OE为∠BOD的平线，∠BOE=15°，求∠AOD和∠BOC的度数.
解:因为OE为∠BOD的平分线，∠BOE=15°， 所以∠BOD=2∠BOE=30°，所以∠AOD=∠AOB+∠BOD= 90°+30°=120°，∠BOC=∠COD-∠BOD=90°-30°=60°.
如图，直线AB，CD相交于点O，OE平分∠AOD，∠COF=90°，∠BOF=40°，求∠AOC和∠DOE的度数.
例6.如图，已知射线OC在∠AOB的内部，OM和ON分别平分∠AOC和∠BOC.(1)若∠AOC=50°，∠BOC=30°，求∠MON的度数;(2)探究∠MON与∠AOB的数量关系.
1.如图，0B，OC是∠AOD内部的两条射线，OM平分∠AOB，ON平分∠COD，∠MON=80°.(1)若∠BOC=40°，则∠AOD的度数为_______；(2)若∠AOD=x°，则∠BOC的度数为___________.(用含x的式子表示)
2.如图，OE，OD分别平分∠AOC和∠BOC.(1)若∠AOB=90°，∠BOC=38°，求∠DOE的度数；
(2)若∠AOB=α，∠BOC=β(∠AOB，∠BOC均为锐角，且α＞β)，其他条件不变，求∠DOE的度数；
(3)从(1)(2)的结果中，你发现了什么规律?请写出来.
(3)∠DOE的大小是∠AOB的大小的一半，与∠BOC的大小无关.
例7.如图，已知OB是∠AOC的平分线，OD是∠COE的平分线，如果∠AOE= 140°，∠BOC比∠COD的2倍还多10°，求∠AOB的度数.
解:设∠COD的度数为x°.因为OD是∠COE的平分线，所以∠COE=2∠COD=(2x)°.因为∠BOC比∠COD的2倍还多10°,所以∠BOC=(2x+10)°.因为OB是∠AOC的平分线，所以∠AOB=∠BOC,∠AOC=2∠BOC=(4x+20)°.
因为∠AOE=140°，∠AOE=∠COE+∠AOC,所以2x+4x+20=140，解得x=20，所以∠AOB=∠BOC=(2x+10)°=50°.所以∠AOB的度数是50°.
1.如图，已知∠AOC:∠BOC=1:4，0D平分∠AOB，且∠COD=33°，求∠AOB的度数.
2.如图，∠AOC:∠COD:∠DOB=2:3:4，OM平分∠AOC，ON平分∠DOB，且∠MON=90°，求∠AOB的度数.
所以∠MON=∠MOC+∠COD+∠NOD=x°+(3x)°+(2x) °=(6x)°.又∠MON= 90°，所以6x=90，所以x=15，所以∠AOB=9×15°=135°.
利用分类讨论思想求角度
例8.已知OC平分∠AOB.若∠AOB=70°，∠COD=10°，则∠AOD的度数为______________.
1.从点O引出三条射线OA，OB，OC，已知∠AOB=30°，在这三条射线中，当其中一条射线是另两条射线所组成角的平分线时，∠AOC的度数为_______________________.
15°或30°或60°
2.已知∠AOB=108°，∠BOC=22°，射线OD，OE分别是∠AOB和∠BOC的平分线，求∠DOE的度数.
分两种情况讨论:(1)当OC在∠AOB内部时，如图①，∠DOE=∠BOD-∠BOE=54°-11°=43°;(2)当OC在∠AOB外部时，如图②,∠DOE=∠BOD+∠BOE=54°+11°=65°.综上所述，∠DOE的度数为43°或65°.