

高中数学人教A版 (2019)必修 第一册1.4 充分条件与必要条件学案及答案
展开教学目标
理解充要条件的意义,会判断简单的充要条件问题,能对充要条件进行证明
【知识点框架】
一、充分必要条件
若p既是q的充分条件,也是q的必要条件,则称p是q的充分必要条件,简称为充要条件(同时也称q是p的充要条件).
注:“p是q的充要条件”中,p是条件,q是结论.
“q是p的充要条件”中,q是条件,p是结论.
思考:
1.命题p和q的条件关系通常有几类?
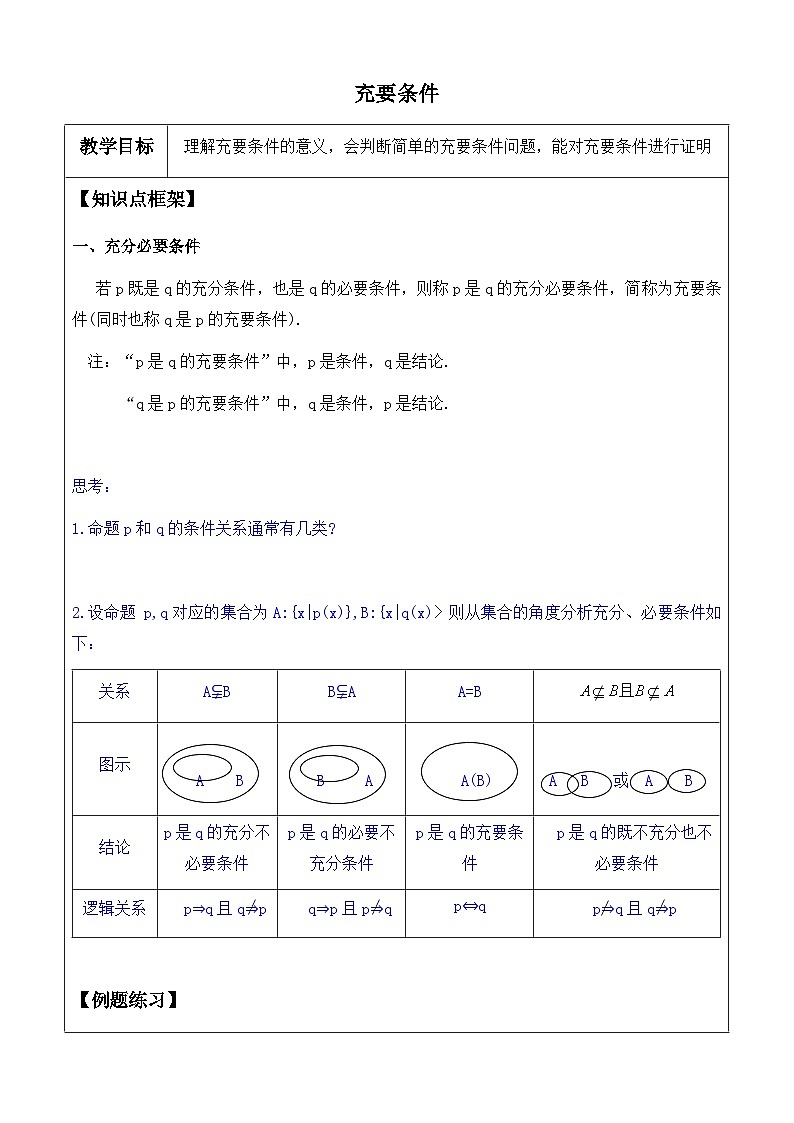
2.设命题 p,q对应的集合为A:{x|p(x)},B:{x|q(x)〉则从集合的角度分析充分、必要条件如下:
关系
A⫋B
B⫋A
A=B
图示
A B
B A
A(B)
A B 或 A B
结论
p是q的充分不必要条件
p是q的必要不充分条件
p是q的充要条件
p是q的既不充分也不必要条件
逻辑关系
p⇒q且q⇒p
q⇒p且p⇒q
p⇔q
p⇒q且q⇒p
【例题练习】
题型一:充要条件的判断
例1.下列各题中,条件p是q的什么条件?(指明充分不必要条件、必要不充分条件、充要条件、既不充分也不必要条件)
(1)p:x>1,q:x²>1;
(2)p:ab=0,q:a²+b²=0;
(3)△ABC中,p:∠A∠>C,q:BC>AB;
(4)p:a>b,q:<1;
(5)p:|x|<2,q:-3
(1)定义法,即把题目中所给条件按逻辑关系画出箭头示意图,再用定义进行判断,这是最常用、最基本的方法.
通常对 p⇒q要予以证明,p⇒q可举反例说明.
(2)集合法,利用集合间包含关系进行判断,常用于一些范围问题.
练习:
1.下列各题中,p是q的什么条件?
(1)p:a=3,q:(a-2)(a-3)=0;
(2)p:四边形的对角线相等,q:四边形是矩形;
(3)p:或,q:;
(4)p:x=|y|,q:x=y;
(5)p:x<3,q:0
例2.使不等式成立的一个充分不必要条件是( )
A. B.
C. D.
总结:
(1)该类问题先找出充要条件,然后根据{充分不必要}⫋{充要}⫋{必要不充分}进行求解.
(2)求充要条件就是求符合题意的参数的范围.
练习:
1.设a∈R,则a>4成立的一个必要不充分条件是( )
A. a>1 B. a<1
C. a>5 D. a<5
2.方程ax²+x+1=0有实根的充要条件是 .
题型三:利用充要条件求参数
例3.已知 p:-2≤x≤10,q:1-m≤x≤1+m(m>0),且p是q的充分不必要条件,则实数m的取值范围为 .
总结:利用充分、必要、充要条件的关系求参数范围的步骤:
(1)化简p,q两命题.
(2)根据p与q的关系(充分、必要、充要条件)转化为集合间的关系.
(3)利用集合间的关系建立不等关系.
(4)求解参数范围.
练习:
1.已知集合A={x|x²-3x+2=0},B={x|x²-mx+2=0},若A是B的必要不充分条件,求实数m的取值范围.
题型四:充要条件的证明
例4.已知ab≠0,求证:a+b=1的充要条件是a³+b³+ab-a²-b²=0.
注:a³+b³=(a+b)·(a²-ab+b²).
总结:充要条件的证明
(1)由题意先确定条件p,结论q.
(2)证p⇒q,得充分性.
(3)证q⇒p,得必要性.
(4)结论成立.
练习:
1.求证:“△ABC是等边三角形”的充要条件是“a²+b²+c²=ab+bc+ca”,a,b,c是△ABC的三边长.
【课后巩固】
1.“x>0”是“x≠0”的( )
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
2.x∈A∪B是x∈A∩B的( )
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
3.“x≠1”是“x²-2x+1≠0”的( )
A.充要条件 B.充分不必要条件
C.必要不充分条件 D.既不充分也不必要条件
4.设A,B 是两个集合,则“A∩B=A”是“A⊆B”的( ).
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
5.设四边形ABCD的两条对角线为AC,BD,则“四边形ABCD为菱形”是“AC⊥BD”的( )
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
高中数学人教A版 (2019)必修 第一册4.3 对数学案: 这是一份高中数学人教A版 (2019)必修 第一册4.3 对数学案,共4页。
高中数学人教A版 (2019)必修 第一册3.3 幂函数导学案及答案: 这是一份高中数学人教A版 (2019)必修 第一册3.3 幂函数导学案及答案,共7页。学案主要包含了幂函数的概念,五个幂函数的图象与性质,幂函数性质的应用等内容,欢迎下载使用。
数学必修 第一册1.4 充分条件与必要条件学案: 这是一份数学必修 第一册1.4 充分条件与必要条件学案,共6页。













