浙教版数学七年级上册 1.4 有理数的大小比较课件

这是一份浙教版数学七年级上册 1.4 有理数的大小比较课件，共18页。

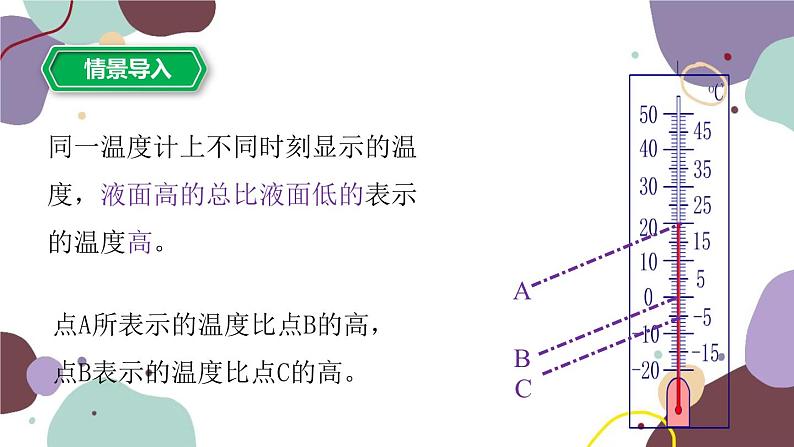
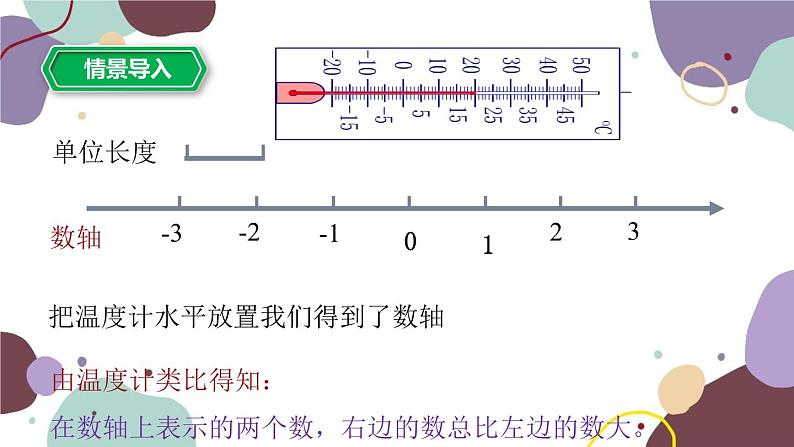
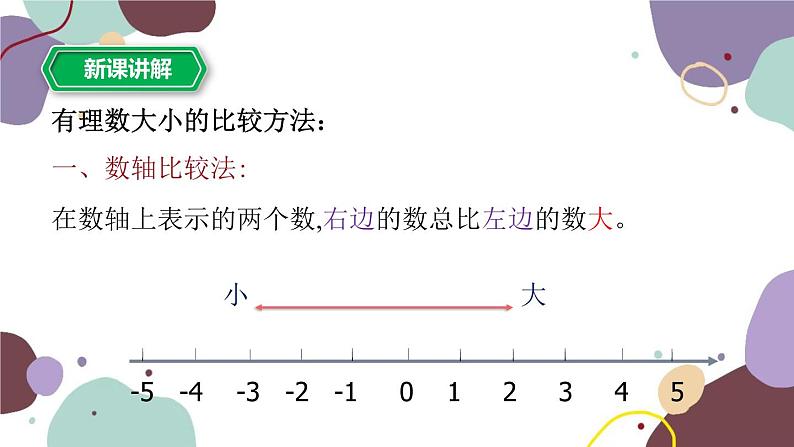
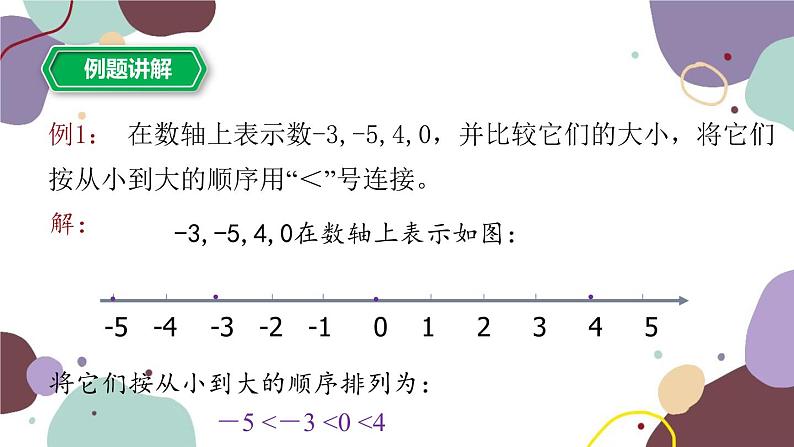
第一章 有理数1.4 有理数的大小比较1.有理数的绝对值的意义：代数意义:一个正数的绝对值是它本身；零的绝对值是零； 一个负数的绝对值是它的相反数。几何意义:一个数在数轴上对应的点到原点的距离 2.绝对值的性质： 3.绝对值与相反数的关系： ｜a｜≥０（非负性）互为相反数的两个数的绝对值相等；绝对值相等，符号相反的两个数互为相反数。请比较下列几组数的大小：><⑵ 2 ___ 7；<⑴ 0.6 ___ 0 ；　⑶ ___ 同一温度计上不同时刻显示的温度，液面高的总比液面低的表示的温度高。ABC点A所表示的温度比点B的高，点B表示的温度比点C的高。把温度计水平放置我们得到了数轴32-3-2-110单位长度数轴由温度计类比得知：在数轴上表示的两个数，右边的数总比左边的数大。有理数大小的比较方法：一、数轴比较法:例1： 在数轴上表示数-3,-5,4,0，并比较它们的大小，将它们按从小到大的顺序用“＜”号连接。解：-3,-5,4,0在数轴上表示如图：将它们按从小到大的顺序排列为：－5 <－3 <0 <4 在数轴上表示下列各对数，并比较它们的大小； ⑴ 2 和 0； 　　　 ⑵－5和－1； ⑶－4 和 0；　 ⑷－2 和 1.5 解：2,0，-5,-1，-4,,-2，1.5在数轴上表示如图：●●●●●由数轴可知： 2 ＞ 0 －5＜－1 －4 ＜ 0 －2 ＜ 1.5有理数比较大小可能会有哪几种情况？正数和零负数和零正数和负数正数和正数负数和负数正数都大于零，负数都小于零，正数大于一切负数。由数轴法可知：想一下这两个怎么比较大小？1、在数轴上表示下列各对数，并比较它们的大小； ⑴2和5； 　　　 ⑵－3和－1； ⑶－4.5和－2；　 ⑷－5和－1.5 2、求上述各对数的绝对值，并比较它们的大小。上面各对数的大小与他们的绝对值的大小有什么关系？解：2,5，-3,-1，-4.5,-2，-5，-1.5在数轴上表示如图：●●●●●●●二、直接比较法：有理数大小的比较方法：2、两个正数比较大小，绝对值大的数大；两个负数比较大小，绝对值大的数反而小。1、正数都大于零，负数都小于零， 正数大于一切负数。例2：比较下列每对数的大小，并说明理由：（1）－8与＋2 ；（2）－0.001与0 ；（3）－ 与－ ；解：（1）－8 ＋2 （2）－0.001 0（负数小于一切正数）（负数都小于零）（两个负数相比，绝对值大的反而小）<<＞ ，∴ - ＜ ->><<<1、利用数轴回答： ⑴有没有最大的整数和最小的整数？⑶有没有最大的负整数和最小的负整数？答：没有最大的正整数，最小的正整数是1。答：都没有。⑵有没有最大的正整数和最小的正整数？答：最大的负整数是－1，没有最小的负整数。4、你能写出绝对值不大于2的所有整数吗？3、求大于－ 4并且小于4.2的所有整数。答：大于－ 4并且小于3.2的整数有： －3，－2，－1，0，1，2，3，4。答：绝对值不大于2的整数有：－2，－1，0，1，2。2、填空：绝对值最小的有理数是 ；绝对值最小的自然数是 ；绝对值最小的负整数是 。00－11、小明在课外书上看到一道习题：“若a表示一个有理数，请比较a与－a的大小”，他觉得太简单了，马上就得出了a> －a的结论，他做得对吗？若a是正数，则a>－a；若a是负数，则a<－a；若a是零，则a＝－a。2、若a>0，b<0，且|a|<|b|，则你能比较a、b、－a、－b这四个数的大小吗？答：b<－a < a <－b（提示：数轴法） 有理数大小的比较方法：一、数轴比较法二、直接比较法：1、 正数都大于零，负数都小于零， 正数大于一切负数。2、两个正数比较大小，绝对值大的数大；两个负数比较大小，绝对值大的数反而小。谢 谢！！