数学八年级上册本节综合课后测评

这是一份数学八年级上册本节综合课后测评，共4页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。

1．若一个三角形的一个外角小于与它相邻的内角，则这个三角形是( )
A．直角三角形B．锐角三角形C．钝角三角形D．无法确定
2．如图，在△ABC中，已知∠A=80°，∠B=60°，DE∥BC，那么∠CED的大小是（ ）
A．40°B．60°C．120°D．140°
3．一把直尺与一块三角板如图放置，若∠1=45°，则∠2的度数为（ ）
A．125°B．135°C．145°D．155°
4．如图，将三角尺的直角顶点放在直尺的一边上，∠1=30°，∠2=50°， 则∠3的度数等于（ ）
A．50°B．30°C．20°D．15°
5．如图，已知直线 l1 、 l2 、 l3 两两相交，且 l1⊥l3 .若 α=50° ，则 β 的度数为（ ）
A．120°B．130°C．140°D．150°
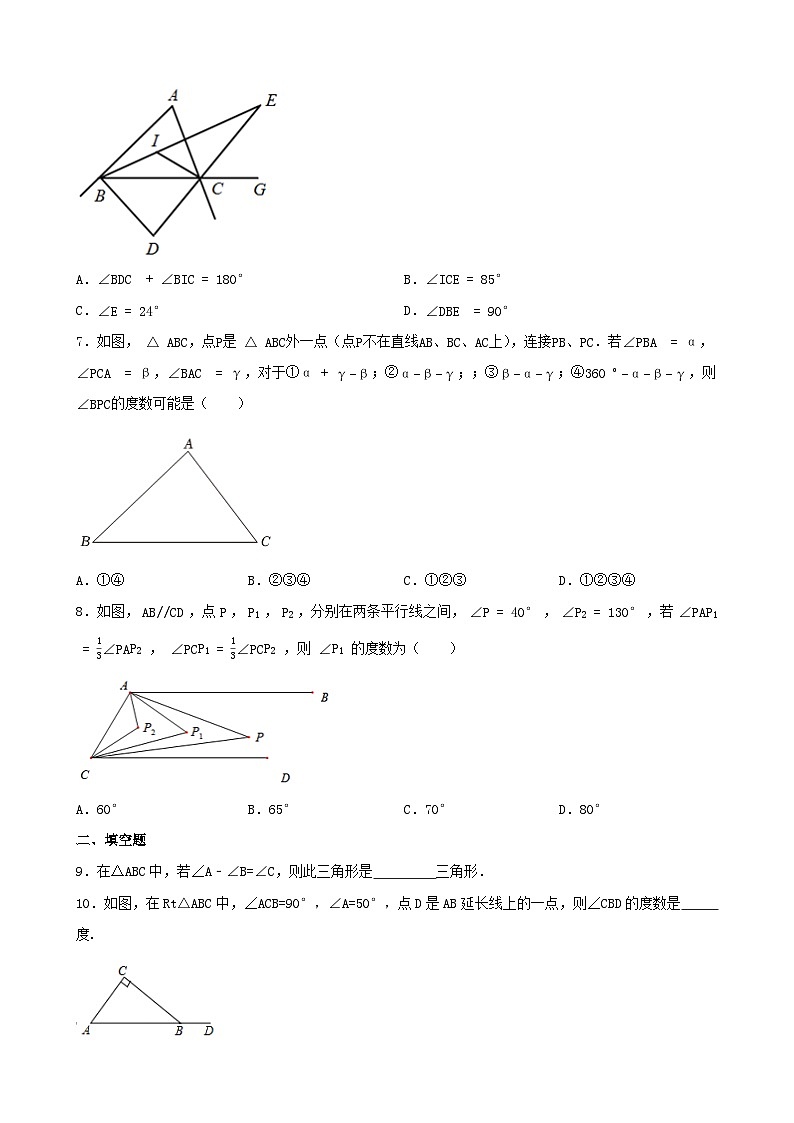
6．如图，在 △ABC 中， ∠BAC=48° ，点 I是 ∠ABC 、 ∠ACB 的平分线的交点．点D是 ∠ABC 、 ∠ACB 的两条外角平分线的交点，点E是内角 ∠ABC 、外角 ∠ACG 的平分线的交点，则下列结论 错误的是（ ）
A．∠BDC+∠BIC=180°B．∠ICE=85°
C．∠E=24°D．∠DBE=90°
7．如图，△ABC，点P是△ABC外一点（点P不在直线AB、BC、AC上），连接PB、PC．若∠PBA=α，∠PCA=β，∠BAC=γ，对于①α+γ−β；②α−β−γ；；③β−α−γ；④360∘−α−β−γ，则∠BPC的度数可能是（ ）
A．①④B．②③④C．①②③D．①②③④
8．如图， AB//CD ，点 P ， P1 ， P2 ，分别在两条平行线之间， ∠P=40° ， ∠P2=130° ，若 ∠PAP1=13∠PAP2 ， ∠PCP1=13∠PCP2 ，则 ∠P1 的度数为（ ）
A．60°B．65°C．70°D．80°
二、填空题
9．在△ABC中，若∠A﹣∠B=∠C，则此三角形是 三角形．
10．如图，在Rt△ABC中，∠ACB=90°，∠A=50°，点D是AB延长线上的一点，则∠CBD的度数是 度.
11．如图，将三角板的直角顶点放在直尺的一边上，∠1＝30°，∠2＝50°，则∠3= °．
12．如图，在 RtΔABC 中， ∠ACB=90°，∠CAB=30° ， ∠ACB 的平分线与 ∠ABC 的外角平分线交于点 E ，则 ∠AEB 的度数为 。
13．如图，点D在AB上，点E在AC上，BE、CD相交于点O，∠A=40°，∠C=30°，∠BOD=100°.则∠B= °.
三、解答题
14．已知：在△ABC中，∠B=∠C，AE是△ABC外角∠DAC的角平分线.求证：AE∥BC.
15．如图，△ABE中，BE是∠DBC的角平分线，求证：∠ACB=∠A+2∠E．
16．如图所示，在△ABC.D是BC边上一点，∠1=∠2，∠3=∠4，∠BAC=63°，求∠DAC的度数．
17．如图，在△ABC中， ∠ACB=90∘ ， CD⊥AB, AF 是角平分线，交CD于点E，证明： ∠1=∠2.
18．如图，在△ABC中，∠C＝90°，点D在AC上，DE∥AB，若∠CDE＝165°，求∠B的度数.
19．如图，已知BC∥DF，∠B=∠D，A、F、B三点共线，连接AC交DF于点E.
（1）求证：∠A=∠ACD；
（2）若FG∥AC，∠A+∠B=106°，求∠EFG的度数.