高中数学人教A版 (2019)必修 第一册3.1 函数的概念及其表示背景图课件ppt

这是一份高中数学人教A版 (2019)必修 第一册3.1 函数的概念及其表示背景图课件ppt，共34页。

1.掌握函数的三种表示法:解析法、列表法、图象法以及各自的优缺点.在解析法中尤其要掌握用换元和代入法求函数的解析式.2.在实际问题中,能够选择恰当的表示法来表示函数.3.能利用函数图象求函数的值域,并确定函数值的变化趋势.
基础落实·必备知识全过关
重难探究·能力素养全提升
成果验收·课堂达标检测
目 录 索 引
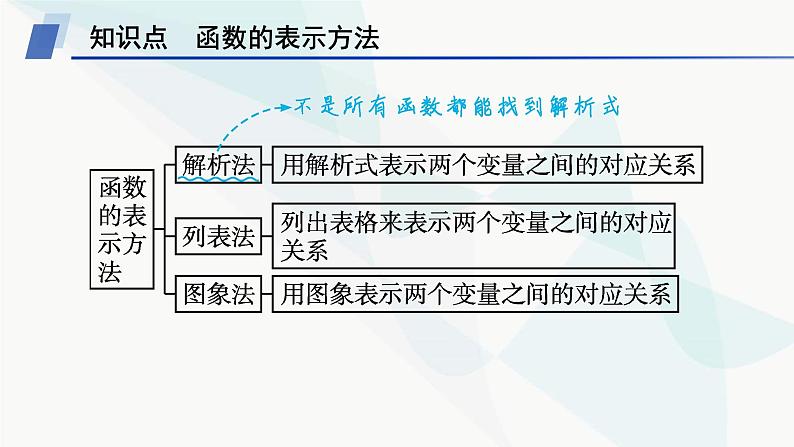
知识点 函数的表示方法
名师点睛函数的三种表示方法的优缺点
过关自诊1.判断正误.(正确的画√,错误的画×)(1)任何一个函数都可以用列表法表示.(　　)(2)任何一个函数都可以用解析法表示.(　　)(3)任何一个函数都可以用图象法表示.(　　)(4)函数的图象一定是一条连续不断的曲线.(　　)(5)函数f(x)=x+1,x∈R与g(x)=x+1,x∈N的图象相同.(　　)
3.[北师大版教材习题]下表列出的是一份数学测试选择题的答案表.
它是使用列表法表示的函数吗?为什么?
解 该答案表不是使用列表法表示的函数,因为题号与正确答案之间不是函数关系.判断依据:函数所研究的两个集合为非空数集,而此题“正确答案”的集合不是数集.
4.[人教B版教材例题]已知函数y= ,指出这个函数的定义域、值域,并作出这个函数的图象.
解 函数的定义域为[0,+∞).由y= 在y≥0时有解可知,函数的值域为[0,+∞).通过描点作图法,可以作出这个函数的图象,如图所示.
探究点一　函数的三种表示法的应用
【例1】 某商场新进了10台彩电,每台售价3 000元,试求售出台数x与收款数y(单位:元)之间的函数关系,分别用列表法、图象法、解析法表示出来.
(2)图象法:(3)解析法:y=3 000x,x∈{1,2,3,…,10}.
规律方法　理解函数表示法注意以下要点:(1)列表法、图象法、解析法均是函数的表示法,无论是哪种方式表示函数,都必须满足函数的概念.(2)列表法更直观形象,图象法从形的角度描述函数,解析法从数的角度描述函数.(3)函数的三种表示法互相兼容或补充,许多函数是可以用三种方法表示的,但在实际操作中,仍以解析法为主.
变式训练1 将一条长为10 cm的铁丝剪成两段,并以每一段铁丝的长度为周长各做一个正方形.试用解析法、列表法、图象法表示两个正方形的面积之和S(单位:cm2)与其中一段铁丝长x(单位:cm,x∈N*)的函数关系.
解 这个函数的定义域为{x|1≤x≤9,x∈N*}.
探究点二　求函数的解析式
【例2】 (1)已知f(x+1)=x2-3x+2,求f(x);(2)已知f(x)是二次函数,且满足f(0)=1,f(x+1)-f(x)=2x,求f(x)的解析式;(3)已知函数f(x)对于任意的x都有f(x)+2f(-x)=3x-2,求f(x).
解 (1)(方法1)令x+1=t,则x=t-1.将x=t-1代入f(x+1)=x2-3x+2,得f(t)=(t-1)2-3(t-1)+2=t2-5t+6,∴f(x)=x2-5x+6.(方法2)∵f(x+1)=x2-3x+2=x2+2x+1-5x-5+6=(x+1)2-5(x+1)+6,∴f(x)=x2-5x+6.
(2)设f(x)=ax2+bx+c(a≠0).∵f(0)=1,∴c=1,则f(x)=ax2+bx+1.∵f(x+1)-f(x)=2x对任意的x∈R都成立,∴a(x+1)2+b(x+1)+1-(ax2+bx+1)=2x,即2ax+a+b=2x,
(3)∵对于任意的x都有f(x)+2f(-x)=3x-2,∴将x替换为-x,得f(-x)+2f(x)=-3x-2,联立方程组消去f(-x),可得f(x)=-3x- .
规律方法　求函数解析式的四种常用方法
变式训练2 (1)已知f(x)是一次函数,且f(f(x))=2x-1,求f(x)的解析式;
解 ∵f(x)为一次函数,∴可设f(x)=ax+b(a≠0).∵f(f(x))=f(ax+b)=a(ax+b)+b=a2x+ab+b=2x-1.
探究点三　利用函数的图象求函数的值域
【例3】 作出下列函数的图象,并求其值域:(1)y=1-x(x∈Z);
解 因为x∈Z,所以函数图象为一条直线上的孤立点(如图①),由图象知,y∈Z.
(2)y=2x2-4x-3(0≤x<3).
解 因为x∈[0,3),所以函数图象是抛物线的一段(如图②),由图象知,y∈[-5,3).
规律方法　函数图象的作法及注意点(1)作函数图象最基本的方法是描点法:主要有三个步骤——列表、描点、连线.作图象时一般先确定函数的定义域,再在定义域内化简函数解析式,最后列表画出图象.(2)函数的图象可能是平滑的曲线,也可能是一群孤立的点,画图时要注意特殊点.如图象与坐标轴的交点、区间端点、二次函数图象的顶点等,还要分清这些特殊点是实心点还是空心圈.如本题(1)中图象是由一些散点构成的,这里不能将其用平滑曲线连起来;本题(2)中描出两个端点及顶点,依据二次函数的图象特征作出函数图象,注意x=3不在定义域内,从而点(3,3)处用空心圈.
变式训练3 作出下列函数的图象,并写出其值域.(1)y=2x+1,x∈[0,2];
解 当x=0时,y=1;当x=1时,y=3;当x=2时,y=5.函数图象过点(0,1),(1,3),(2,5).图象如图所示.由图可知,函数的值域为[1,5].
由图可知,函数的值域为(0,1].
本节要点归纳1.知识清单:(1)函数的表示法.(2)求函数解析式.(3)函数图象的应用.2.方法归纳:待定系数法、换元法、配凑法、数形结合法.3.常见误区:求函数解析式或画函数图象时易忽视函数定义域.
1.将长度为2的一根铁丝折成长为x的矩形,矩形的面积y关于x的函数关系式是y=x(1-x),则函数的定义域为(　　)A.RB.{x|x>0}C.{x|02.已知一次函数的图象过点(1,0)和(0,1),则该一次函数的解析式为(　　)A.f(x)=-xB.f(x)=x-1C.f(x)=x+1D.f(x)=-x+1
3.某天早上,小明骑车上学,出发时感到时间较紧,然后加速前进,后来发现时间还比较充裕,于是放慢了速度,与以上事件吻合得最好的图象是(　　)
解析 因为选项A,D第一段都是匀速前进,不合题意,故排除选项A,D,首先加速前进,然后放慢速度,说明图象上升的速度先快后慢,故选C.
4.(1)已知函数f(x+1)=3x+2,求f(x);
解 (方法1　换元法)令x+1=t,∴x=t-1,∴f(t)=3(t-1)+2=3t-1,∴f(x)=3x-1.(方法2　配凑法)f(x+1)=3x+2=3(x+1)-1,∴f(x)=3x-1.