高中数学人教A版 (2019)必修 第一册4.2 指数函数说课课件ppt

这是一份高中数学人教A版 (2019)必修 第一册4.2 指数函数说课课件ppt，共36页。

1.通过具体实例,了解指数函数的实际意义,理解指数函数的概念.2.能用描点法或借助计算工具画出具体指数函数的图象,探索并理解指数函数的单调性与特殊点.3.能够应用指数函数的图象及性质解决问题.
基础落实·必备知识全过关
重难探究·能力素养全提升
成果验收·课堂达标检测
目 录 索 引
知识点1 指数函数的概念
1.一般地,函数y=ax(a>0,且a≠1)叫做指数函数.其中指数x是自变量,定义域为R.2.指数函数的特征:(1)底数a>0,且a≠1;(2)指数幂的系数是1.名师点睛根据指数函数的定义,只有形如y=ax(a>0,且a≠1)的函数才叫指数函数,
过关自诊1.指数函数为什么要规定a>0,且a≠1?
提示 如果a<0,那么ax对某些x值没有意义,如 无意义;如果a=0,那么当x>0时,ax=0,当x≤0时,ax无意义;如果a=1,y=1x=1是个常数函数,没有研究的必要.所以规定a>0,且a≠1,此时x可以是任意实数.
2.给出下列函数:①y=2·3x;②y=3x+1;③y=3x;④y=x3;⑤y=(-2)x.其中,指数函数的个数是(　　)A.0B.1C.2D.4
解析 只有③是指数函数.故选B.
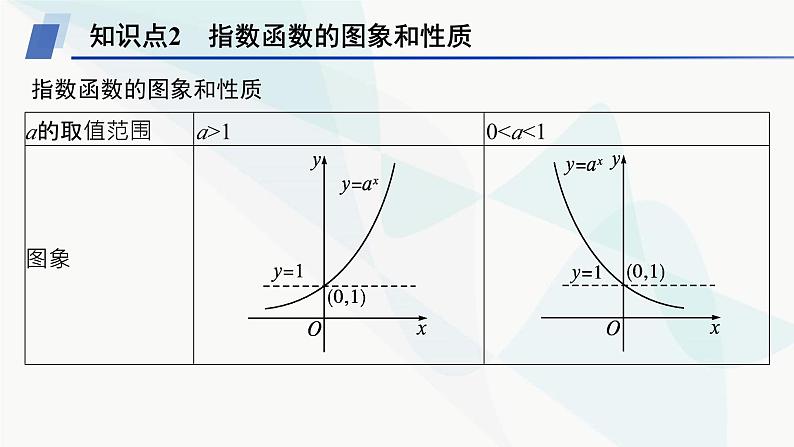
知识点2 指数函数的图象和性质
指数函数的图象和性质
过关自诊1.指数函数y=ax(a>0,且a≠1)的图象“升”“降”主要取决于什么?具体变化特征是什么?
2.指数函数y=5x的定义域是　　　　　,值域是　　　　　. 
提示 指数函数y=ax(a>0,且a≠1)的图象“升”“降”主要取决于字母a.当a>1时,图象具有上升趋势,当x>0时,底数a的值越大,函数图象“越陡”,函数值增长得越快;当0解析 由指数函数y=5x的图象和性质可知定义域为R,值域为(0,+∞).
3.[人教B版教材例题]利用指数函数的性质,比较下列各题中两个值的大小:(1)0.8-0.1与0.8-0.2;
(2)2.5a与2.5a+1.
解 0.8-0.1与0.8-0.2都是以0.8为底的幂值,由于y=0.8x这个函数在实数集R上是减函数,且-0.1>-0.2,所以0.8-0.1<0.8-0.2.
解 2.5a与2.5a+1都是以2.5为底的幂值,由于y=2.5x这个函数在实数集R上是增函数,且a探究点一　指数函数的概念
【例1】 (1)如果指数函数y=f(x)的图象经过点 ,那么f(4)f(2)等于　　　　　. 
(2)已知函数y=(a2-3a+3)ax是指数函数,求a的值.
规律方法　指数函数是一个形式定义,其特征如下:
变式训练1 下列以x为自变量的函数中,是指数函数的为(　　)A.y=(π-1)xB.y=(1-π)xC.y=3x+1D.y=x2
解析 π-1为正实数,A是指数函数;B式中,1-π<0,B不是指数函数;C式中,指数位置不是x,C不是指数函数;D式中,自变量不在指数上,D不是指数函数.
探究点二　指数函数的图象的应用
角度1.指数型函数图象过定点问题【例2】 已知函数f(x)=ax+1+3(a>0,且a≠1)的图象一定过点P,则点P的坐标是　　　　　. 
解析 当x+1=0,即x=-1时,f(-1)=a0+3=4恒成立,故函数f(x)=ax+1+3的图象恒过点(-1,4).
变式探究 本例中的函数改为f(x)=5a3x-2+3后,求f(x)的图象过的定点坐标.
规律方法　指数型函数图象过定点问题的解法因为函数y=ax(a>0,且a≠1)的图象恒过定点(0,1),所以对于函数f(x)=kag(x)+b(k,a,b均为常数,且k≠0,a>0,且a≠1),若g(m)=0,则f(x)的图象过定点(m,k+b).
角度2.指数型函数图象的识别【例3】 函数f(x)=ax-b的图象如图所示,其中a,b为常数,则下列结论正确的是(　　)A.a>1,b<0B.a>1,b>0C.00D.0解析 由于f(x)的图象单调递减,所以00,b<0.故选D.
规律方法　指数型函数图象问题的处理技巧(1)抓住图象上的特殊点,如指数函数的图象过定点、特殊点的函数的值的符号等;(2)利用图象变换,如函数图象的平移变换(左右平移、上下平移);(3)利用函数的奇偶性与单调性,奇偶性确定函数的对称情况,单调性决定函数图象的走势.
变式训练2 [北师大版教材习题]已知三个指数函数y=ax,y=bx,y=cx的图象如图.(1)试比较a,b,c的大小;(2)指数函数的底数越大,它的图象与直线x=1的交点的纵坐标是越大还是趋近于0?
解 (1)观察图象可知,当x=1时,c1>b1>a1,即c>b>a.(2)底数越大,图象与直线x=1的交点的纵坐标越大.
角度3.画指数型函数的图象【例4】 画出函数y= 的图象,这个图象有什么特征?你能根据图象指出它的值域和单调区间吗?
∴原函数的图象关于y轴对称.由图象可知值域是(0,1],单调递增区间是(-∞,0],单调递减区间是(0,+∞).
规律方法　指数函数y=ax与y= (a>0,且a≠1)的图象关于y轴对称.处理函数图象问题的常用方法:一是抓住图象上的特殊点;二是利用图象的变换;三是利用函数的奇偶性与单调性.
变式训练3 画出下列函数的图象,并说明它们是由函数y=2x的图象经过怎样的变换得到的.(1)y=2x-1;(2)y=2x+1;(3)y=-2x;(4)y=2|x|.
解 (1)如图①,y=2x-1的图象是由y=2x的图象向右平移1个单位长度得到的.(2)如图①,y=2x+1的图象是由y=2x的图象向上平移1个单位长度得到的.(3)如图①,y=-2x的图象与y=2x的图象关于x轴对称.(4)函数y=2|x|为偶函数,图象关于y轴对称,且其在x≥0上的图象与y=2x的图象一致,可得y=2|x|的图象如图②所示.
探究点三　利用指数函数的单调性比较幂值大小
【例5】 [2023江苏无锡期末]已知a=2.1-0.1,b=1.2-0.1,c=2.1-0.2,则a,b,c的大小关系为(　　)A.b>c>aB.b>a>cC.a>b>cD.a>c>b
解析 ∵a=2.1-0.1,b=1.2-0.1,c=2.1-0.2,函数y=2.1x是R上的增函数,∴a>c.而y=x-0.1在(0,+∞)上单调递减,∴aa>c.故选B.
规律方法　比较幂的大小的常用方法
变式训练4 (多选题)下列式子不正确的是(　　)
解析 由指数函数的单调性可知1.52.5<1.53.2,则A错误;由指数函数的单调性可知1.70.2>1.70=1,0.92.1<0.90=1,即1.70.2>0.92.1,则B错误;
由幂函数、指数函数的单调性可知0.80.5<0.80.4,0.80.4<0.90.4,即0.80.5<0.90.4,则D正确.故选AB.
本节要点归纳1.知识清单:(1)指数函数的概念.(2)指数函数的图象和性质.2.方法归纳:待定系数法、数形结合法.3.常见误区:易忽视底数a的限制条件;易忽视对于a是否大于1进行讨论.
1.给出下列函数:①y=x5;②y=-2x;③y=2x;④y=2x+1;⑤y=3·2x.其中指数函数的个数是(　　)A.1B.2C.3D.4
解析 指数函数是形如y=ax(a>0,且a≠1)的函数,故只有③y=2x是指数函数,①为幂函数,②④⑤都称为指数型函数,所以正确选项为A.
2.函数y=2-x的大致图象是(　　)
A.(-∞,-1]B.(0,+∞)C.(-1,0)D.(-∞,0)
解析 ∵函数f(x)在(-∞,0)上单调递减,在(0,+∞)上是常数,
A.a>b>cB.c>a>bC.b>c>aD.a>c>b
又a=2π>1,∴a>c>b.故选D.
5.若a>3,则函数f(x)=4(a-2)2x+6-1的图象恒过定点　　　　　. 
解析 ∵a>3,∴a-2>1.令2x+6=0,得x=-3,则f(-3)=4(a-2)0-1=3.故函数f(x)的图象恒过定点(-3,3).