八年级上册13.3.1 等腰三角形说课课件ppt

这是一份八年级上册13.3.1 等腰三角形说课课件ppt，共30页。PPT课件主要包含了探究这个三角形的特点，三角形的边，三角形的角，与三角形的有关线段，三角形的对称性，三角形的边和角，ABAC，∠B∠C，等腰△ABC，底角相等等内容，欢迎下载使用。

在故宫博物馆中，有很多建筑设计成等腰三角形，例如下图的中和殿的屋檐设计，你能说说为什么吗？
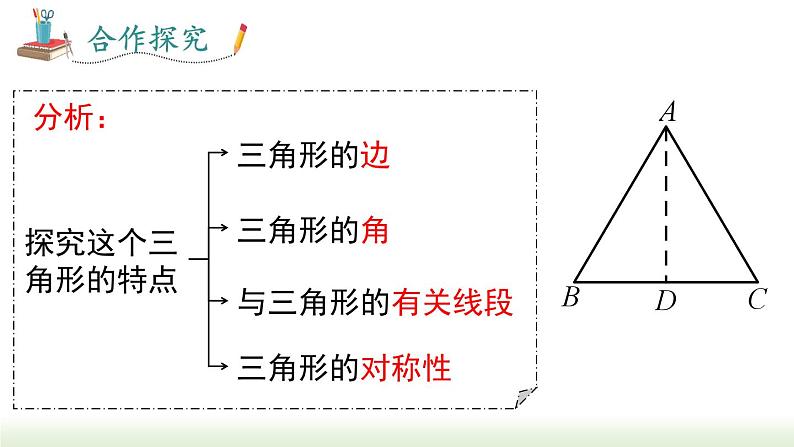
知识点:等腰三角形的性质
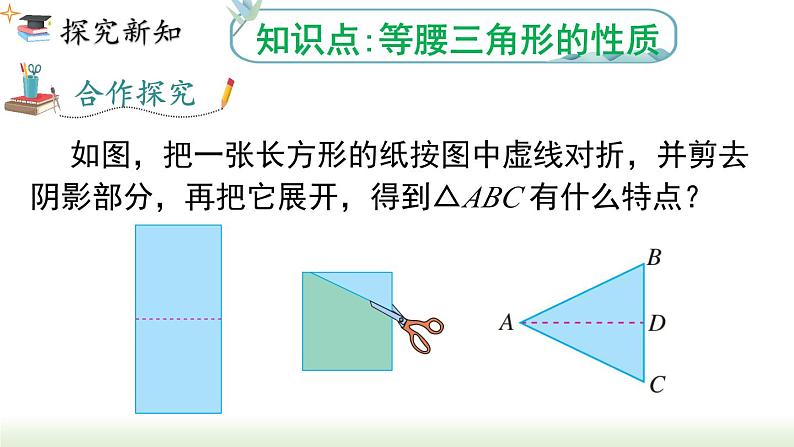
如图，把一张长方形的纸按图中虚线对折，并剪去阴影部分，再把它展开，得到△ABC 有什么特点？
A B D C
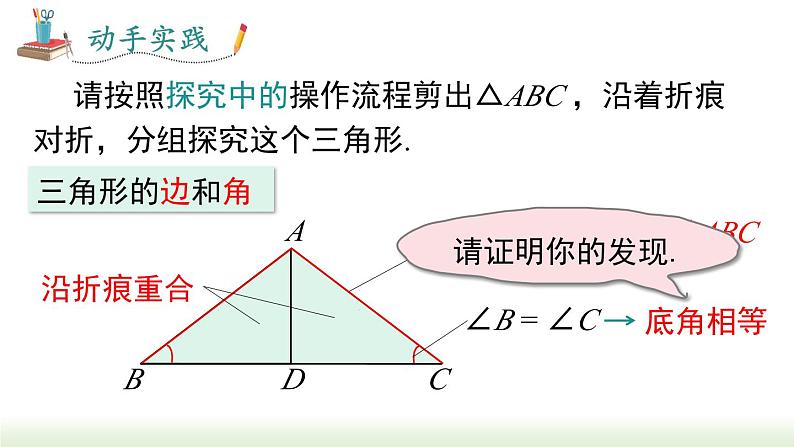
请按照探究中的操作流程剪出△ABC ，沿着折痕对折，分组探究这个三角形.
证明：等腰三角形的性质1：等腰三角形的两个底角相等.
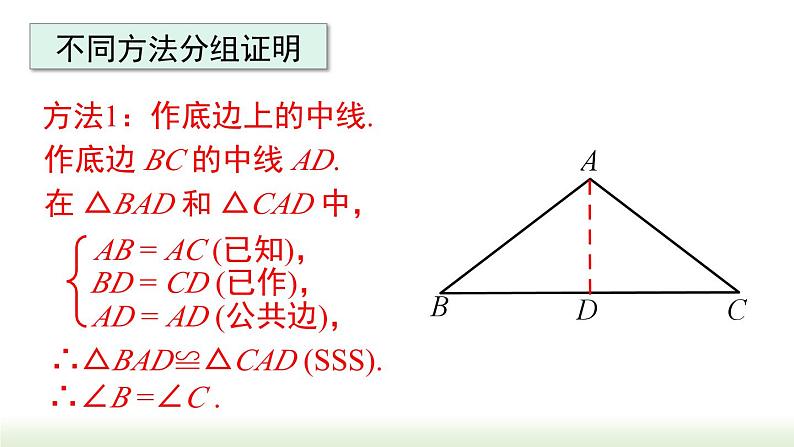
已知：如图，在△ABC 中，AB = AC.求证：∠B = ∠C.
作底边 BC 的中线 AD.
AB = AC (已知)，
BD = CD (已作)，
AD = AD (公共边)，
∴△BAD≌△CAD (SSS).
在 △BAD 和 △CAD 中，
方法1：作底边上的中线.
在 Rt△ABD 与 Rt△ACD 中， AB＝AC (已知)， AD＝AD (公共边)，
方法2：作底边上的高线.
∴ Rt△ABD≌Rt△ACD (HL).
∴∠ADB＝∠ADC＝90°.
在 △ABD 与 △ACD 中， AB＝AC (已知)， ∠BAD＝∠CAD， AD＝AD (公共边)，
∵ AD 是 ∠BAC 的角平分线，
方法3：作顶角的角平分线 AD.
∴ △ABD≌△ACD (SAS).
∴∠BAD＝∠CAD.
等腰三角形的性质1：等腰三角形的两个底角______
(简写成“等边对等角”).
∵ △ABC 是等腰三角形，
∴ ____=____(等角对等边).
1. (淄博)某城市几条道路的位置关系如图所示，道路 AB∥CD，道路 AB 与 AE 的夹角∠BAE＝50°.城市规划部门想新修一条道路 CE，要求 CF＝EF，则 ∠E 的度数为 ( )A. 23°B. 25° C. 27°D. 30°
在上述不同方法的证明过程中，由三角形顶角作的底边上的中线、高线、顶角角平分线有什么特点？
证明：等腰三角形的性质2：等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合.
已知：如图，在△ABC 中，AB = AC，BD = DC，求证 AD⊥BC，DA 平分∠BAC.
假设任意一种线段为已知条件
证明：∵AB = AC，BD = DC，
∴∠ADB = ∠ADC = 90°.
∵∠ADB + ∠ADC = 180°，
∴ ∠BAD = ∠CAD，∠ADB = ∠ADC.
这三条线是否在任意边上都重合？
等腰三角形的性质2：等腰三角形的顶角平分线、底边上的中线、底边上的高_________
(简写成“三线合一”，注意：腰上的高
和中线与底角的平分线不具有这一性质.).
“三线合一”几何语言：
(1)∵△ABC是等腰三角形， BD = CD (已知)∴______________，________ (等腰三角形的“三线合一”)(2)∵△ABC是等腰三角形，∠BAD＝∠CAD (已知)∴_________，AD⊥BC，_________________________ (3)∵△ABC 是等腰三角形，AD⊥BC∴BD = CD，______________(等腰三角形的“三线合一”)
(等腰三角形的“三线合一”)
例1 如图，在△ABC 中，AB = AC，点 D 在 AC 上，且 BD = BC = AD，求 △ABC 各角的度数.
解：∵ AB = AC，BD = BC = AD，
∴∠A = 36°，∠ABC =∠C = 72°.
解得 x = 36°.
于是在△ABC 中，有∠A +∠ABC +∠C = x + 2x + 2x = 180°，
从而∠ABC =∠C =∠BDC = 2x.
设∠A = x，则∠BDC =∠A +∠ABD = 2x，
∴∠ABC =∠C =∠BDC，∠A =∠ABD.
例2 已知点 D、E 在△ABC 的边 BC 上，AB＝AC.(1) 如图①，若 AD＝AE，求证：BD＝CE；(2) 如图②，若 BD＝CE，F 为 DE 的中点，求证： AF⊥BC.
证明：(1) 如图①，过 A 作 AG⊥BC 于 G.
∴ BD＋DF＝CE＋EF.
(2) ∵ BD＝CE，F 为 DE 的中点，
∴ BG－DG＝CG－EG.
∴ BG＝CG，DG＝EG.
∵ AB＝AC，AD＝AE，
等腰三角形的_________________ _____________________________简称“________”
等腰三角形是___对称图形
有_________的三角形
等腰三角形的两个底角_____简称“___________”
顶角平分线、底边上的中线、底边上的高相互重合
1. 等腰三角形的一个角为 70° ，则这个等腰三角形的顶角是 ( )A. 70°B. 40° C. 55° 或 70°D. 70° 或 40°
2.如图，已知 OA＝OB＝OC，且∠ACB＝25°，求 ∠AOB 的大小．
解：∵OA＝OB＝OC，
∴ x＋∠AOB＝x＋25°＋25°.∴∠AOB＝50°.
∵∠A＋∠AOB＝∠ADB＝∠B＋∠ACB.
∴∠B＝∠OCB＝∠OCA＋∠ACB＝x＋25°.
设∠A＝∠OCA＝x，
∴∠A＝∠OCA，∠B＝∠OCB.
(2) 如果把以上“问题”中的条件“∠B = 45°”去掉，再将“∠BAE = 90°”改为“∠BAE = n°”其余条件不变求∠DAC 的度数.
3. (1) 等腰三角形一个底角为 75°，它的另外两个角的度数为__________； (2) 等腰三角形的一个角为 36°，它的另外两个角的度数为____________________； (3) 等腰三角形的一个角为 120°，它的另外两个角的度数为__________.
4.如图，已知 AB＝AC，D 是 BC 边上的中点，求 ∠B＝ 30°，求 ∠BAD 和 ∠ADC 的度数．
∴AD⊥BC (三线合一)，
D 是 BC 边上的中点，
∴∠BAD＝∠ADC－∠B
＝90°－30°＝60°
1. 古代测量水平线的仪器是由一个等腰三角形以及悬挂在顶点处的铅垂线组成.如图 (1) 所示，仪器中三角形的底边猜测是用绳子做成的，因为绳子的中点非常容易确定.测量时，调整底边的位置，如果铅垂线经过底边中点，就表明底边垂直于铅垂线，即底边是水平的，这就是古代的水准仪.(1) 请运用所学的等腰三角形的性质解释古代水准仪的原理；