人教版八年级上册13.3.2 等边三角形图片ppt课件

这是一份人教版八年级上册13.3.2 等边三角形图片ppt课件，文件包含1332第1课时等边三角形的性质和判定pptx、1332第1课时已知底边绘制等腰三角形mp4等2份课件配套教学资源，其中PPT共20页， 欢迎下载使用。

在上节课基础上，需要设计一个等腰△ABC，目前已知底边 BC ，你该如何设计呢？在设计过程中，你有什么发现？
知识点1:等边三角形的性质
探究一 顶点 A 在边 BC 的垂直平分线上运动的过程中，会构成什么特殊的三角形吗？
等边三角形的定义：是三边都_____的特殊的等腰三角形.
等边三角形是特殊的等腰三角形，把等腰三角形的性质用于等边三角形，能得到什么结论？
等腰三角形的性质1：等边对等角. 等边三角形的性质：？
三角形内角和为180°
∠A=∠B=∠C=60°
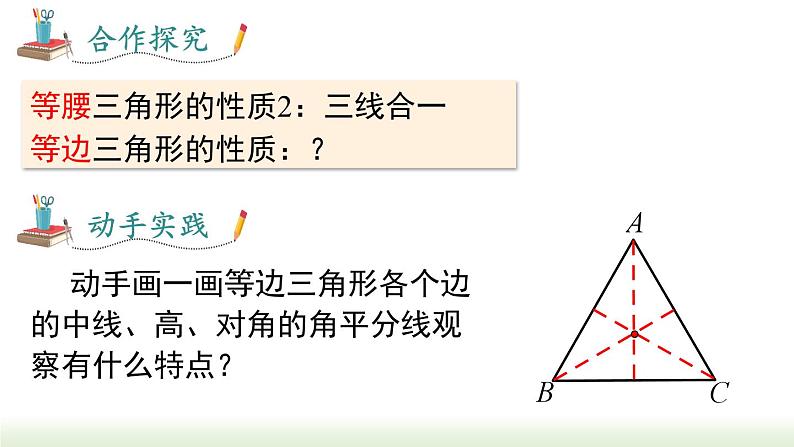
等腰三角形的性质2：三线合一 等边三角形的性质：？
动手画一画等边三角形各个边的中线、高、对角的角平分线观察有什么特点？
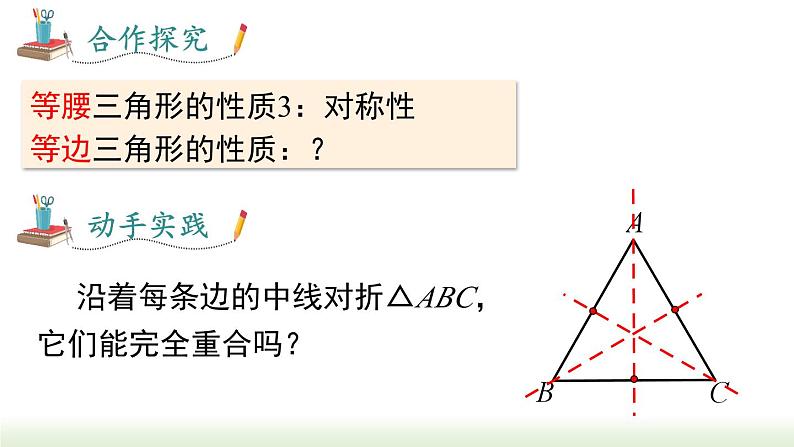
等腰三角形的性质3：对称性 等边三角形的性质：？
沿着每条边的中线对折△ABC，它们能完全重合吗？
每一边上的中线、高和这一边所对的角的平分线互相重合
三个角都相等，且都是 60°
底边上的中线、高和顶角的平分线互相重合
根据刚才的探究，填空：
1.(西峰区期末)如图，AD 是等边△ABC 的中线，AE = AD，求∠EDC 的度数.
解：∵ AD 是等边△ABC 的中线，
∴ AD ⊥ BC，∠BAD =∠CAD =
∴∠ADC = 90°.
∴∠EDC=∠ADC- ∠ADE=15°.
探究二 对于一般△ABC，如何判定这个三角形是等边三角形，请提出猜想并验证.
知识点2:等边三角形的判定
两角相等(等腰三角形的判定)
三边相等(等边三角形的定义)
已知：如图，在△ABC 中，∠A = ∠B = ∠C.求证：△ABC 是等边三角形.
证明：∵∠A = ∠B ，
∴ AB = AC = BC.
∴ △ABC 是等边三角形.
等边三角形的判定方法：
3. 有一个角是______的等腰三角形是等边三角形.
2. 三个角都______的三角形是等边三角形；
1. 三边都______的三角形是等边三角形；
例1 如图，在等边三角形 ABC 中，DE∥BC.求证：△ADE 是等边三角形.
∵△ABC 是等边三角形，
∴∠A =∠B =∠C.
∴∠ADE = ∠B，∠AED = ∠C.
∴∠A = ∠ADE = ∠AED.
∴△ADE 是等边三角形.
想一想：本题还有其他证法吗？
1.(宜昌)如图，在一个池塘两旁有一条笔直小路(BC 为小路端点)和一棵小树(A 为小树位置).测得的相关数据为：∠ABC = 60°，∠ACB = 60°，BC = 48 米，则 AC = _____米.
__________的三角形等边三角形
____________的三角形是等边三角形
等边三角形的三个内角______，并且每一个内角________
有____个角是___的______三角形是等边三角形
(3)一腰上的高也是这条腰上的中线的等腰三角形是等边三角形 ( ).
1.判断下列说法是否正确，如果正确，在括号内填人“√”；如果错误，在括号内填入“×”，并说明理由.
(1)有一个角是 60° 的三角形是等边三角形；( )
(2)有两个内角都等于 60° 的三角形是等边三角形；( )
3.如(1)是一把折叠椅实物图，支架 AB 与 CD 交干点 O，OD = OB，如图(2)是椅子打开时的侧面示意图(忽略材料的厚度)，椅面 MN 与地面水平线 l 平行，BD = 2AC.∠BOD = 60°，BD ≈ 24.70 cm 那么折叠后椅子的高度约为______cm.(结果保留小数点后两位)