人教版八年级上册13.3.1 等腰三角形教案设计

13.3.1《等腰三角形(2)》教案

一、教学目标

(一)知识与技能：1.探索等腰三角形判定定理；2.理解等腰三角形的判定定理，并会运用其进行简单的证明；3.了解等腰三角形的尺规作图.

(二)过程与方法：通过独立思考，交流讨论，发展推理能力和运用数学知识解决实际问题的能力.

(三)情感态度与价值观：学生在探索问题的过程中，体验解决问题的方法和乐趣，增强学习数学的兴趣.

二、教学重点、难点

重点：理解和运用等腰三角形的判定定理.

难点：利用尺规作等腰三角形：已知底边及底边上的高作等腰三角形.

三、教学过程

思考

    我们知道，如果一个三角形有两条边相等，那么它们所对的角相等. 反过来，如果一个三角形有两个角相等，那么它们所对的边有什么关系？

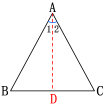如图，在△ABC中，∠B=∠C.
作△ABC的角平分线AD.
在△BAD与△CAD中，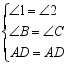

∴ △BAD≌△CAD (AAS)
∴ AB=AC

等腰三角形判定定理：

如果一个三角形有两个角相等，那么这两个角所对的边也相等

(简写成“等角对等边”).

定理应用格式：

∵ ∠B=∠C

∴ AB=AC

例2 求证：如果三角形一个外角的平分线平行于三角形的一边，那么这个三角形是等腰三角形.

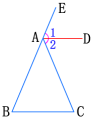已知：如图，∠CAE是△ABC的外角，∠1=∠2，AD∥BC.
求证：AB=AC.
分析：要证明AB=AC，可先证明∠B=∠C. 因为∠1=∠2，所以可以设法找出∠B，∠C与∠1，∠2的关系.
证明：∵ AD∥AC
∴ ∠1=∠B (_______________________)
   ∠2=∠C (_______________________)
又∵ ∠1=∠2
∴ ∠B=∠C
∴ AB=AC (____________)

思考

(1)已知三角形的一条边及这条边上的高，你能作出三角形吗？如果能，能作几个？所作的三角形都全等吗？

已知：三角形的一条边a和这边上的高h.
求作：△ABC，使AB=a，AB边上的高为h.

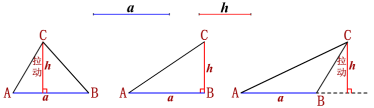
(2)如果已知是等腰三角形的底边及底边上的高，你能用尺规作出等腰三角形吗？能作几个？

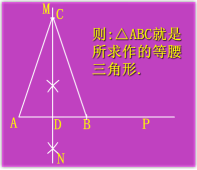
例3 已知等腰三角形底边长为a，底边上的高的长为h，求作这个等腰三角形.

作法：
1.作线段AB=a；
2.作线段AB的垂直平分线MN，与AB相交于点D；
3.在MN上取一点C，使DC=h；
4.连接AC，BC.

练习

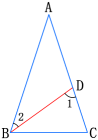1.如图，∠A=36°，∠DBC=36°，∠C=72°.分别计算∠1，∠2的度数，并说明图中有哪些等腰三角形.

解：∵ 在△BCD中，∠C=72°，∠DBC=36°
∴ ∠1=180°-36°-72°=72°
又∵ ∠1是△ABD的外角
∴ ∠2=∠1-∠A=36°
∴ ∠ABC=∠2+∠DBC=72°
因此，由∠ABC=∠C=72°，得△ABC是等腰三角形；由∠1=∠C=72°，得△BCD是等腰三角形；由∠2=∠A=36°，得△ABD是等腰三角形.

2.如图，把一张长方形的纸沿对角线折叠，重合部分是一个等腰三角形吗？为什么？

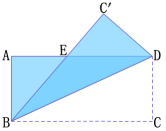解：△BED是等腰三角形. 理由如下：
∵ △BC′D与△BCD关于直线BD对称
∴ △BC′D≌△BCD
∴ ∠C′BD=∠CBD
又∵ AD∥BC
∴ ∠ADB=∠CBD
∴ ∠ADB=∠C′BD
∴ EB=ED
即△BED是等腰三角形.

3.求证：如果三角形一条边上的中线等于这条边的一半，那么这个三角形是直角三角形.

已知：如图，△ABC中，CD是AB边上的中线，且CD=AB.
求证：△ABC是直角三角形.

证明：∵ CD是AB边上的中线，且CD=AB
∴ AD=CD=BD
∴ ∠A=∠ACD，∠B=∠BCD
∵ ∠A+∠B+∠ACD+∠BCD=180°
∴ ∠ACD+∠BCD=90°
即∠ACB=90°
∴ △ABC是直角三角形.

4.如图，AC和BD相交于点O，且AB∥DC，OA=OB，求证：OC=OD.

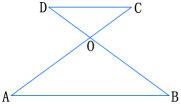证明：∵ AB∥DC

∴ ∠A=∠C，∠B=∠D

又∵ OA=OB

∴ ∠A=∠B

∴ ∠C=∠D

∴ OC=OD

课堂小结

1.本节课你有哪些收获？2.还有没解决的问题吗？

四、教学反思

    学生通过回顾总结等腰三角形的性质为学习等腰三角形的判定做了知识铺垫. 之后将本节课的教学目标展示给学生，让学生做到心中有数，让学生带着问题看书，加强自主探索的能力. 通过学生观察、思考例题，自然地渗透分类讨论的数学解题思想. 通过课堂小结，让学生归纳比较等腰三角形的性质和判定的区别，同时将等腰三角形的性质定理与判定定理有机的结合起来，重在培养学生对两个知识点的综合运用，鼓励学生积极思考. 整节课的目标基本实现，重点难点落实得比较到位，唯一欠缺的是时间有点紧，课堂小结比较仓促.