





2022-2023学年度吉林省长市东北师大附中明珠学校九年级上学期11月月考数学试题
展开初三年级综合测试数学学科试卷
考试时长:120分钟 试卷分值:120分
一、选择题(本大题共8小题,每小题3分.共24分)
1. 已知一元二次方程![]() 有一个根为
有一个根为![]() ,则k的值为( )
,则k的值为( )
A. 1 B. 3 C. ![]() D.
D. ![]()
2. 一元二次方程![]() 根的判别式的值为( )
根的判别式的值为( )
A. 8 B. ![]() C.
C. ![]() D.
D. ![]()
3. 抛物线![]() 的顶点坐标是( )
的顶点坐标是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
4. 如图,![]() 是
是![]() 的直径,
的直径,![]() ,
,![]() ,则
,则![]() 的大小为( )
的大小为( )
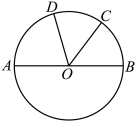
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
5. 将抛物线![]() 先向左平移3个单位长度,再向下平移2个单位长度,得到的抛物线的解析式是( )
先向左平移3个单位长度,再向下平移2个单位长度,得到的抛物线的解析式是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
6. 如图,![]() 内接于
内接于![]() ,连结
,连结![]() ,若
,若![]() ,则
,则![]() 的大小为( )
的大小为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
7. 已知点![]() ,
,![]() 是抛物线
是抛物线![]() 上的点,则( )
上的点,则( )
A. ![]() B.
B. ![]() C.
C. ![]() D. 无法确定
D. 无法确定
8. 如图,抛物线![]() 的顶点在
的顶点在![]() 的边
的边![]() 所在的直线上运动,
所在的直线上运动,![]() 的顶点A的坐标为
的顶点A的坐标为![]() ,点B的坐标为
,点B的坐标为![]() ,若抛物线与
,若抛物线与![]() 的边
的边![]() 、
、![]() 都有公共点,则h的取值范围是( )
都有公共点,则h的取值范围是( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
二、填空题(本大题共6小题.每小题3分,共18分)
9. 在函数![]() 中,当x>1时,y随x的增大而 ___.(填“增大”或“减小”)
中,当x>1时,y随x的增大而 ___.(填“增大”或“减小”)
10. 已知![]() 的半径为
的半径为![]() ,若点
,若点![]() 在
在![]() 内,写出一个
内,写出一个![]() 长的可能值___________.
长的可能值___________.
11. 如图,四边形ABCD是![]() 的内接四边形,若
的内接四边形,若![]() ,则
,则![]() 的大小为___________度.
的大小为___________度.
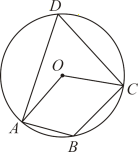
12. 若a是方程![]()
根,则
![]() ___________.
___________.
13. 如图,已知二次函数![]() 与一次函数
与一次函数![]() 的图象相交于点A(-2,6)和B(8,3),则能使
的图象相交于点A(-2,6)和B(8,3),则能使![]() ﹤y2成立的
﹤y2成立的![]() 的取值范围____________ .
的取值范围____________ .
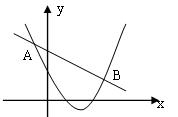
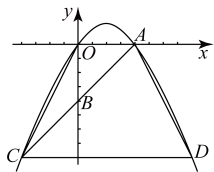
14. 如图,在平面直角坐标系中,抛物线![]() 与x轴正半轴交于点A,点B是y轴负半轴上一点,点A关于点B的对称点C恰好落在抛物线上,过点C作
与x轴正半轴交于点A,点B是y轴负半轴上一点,点A关于点B的对称点C恰好落在抛物线上,过点C作![]() 轴,交抛物线于点D,连结
轴,交抛物线于点D,连结![]() 、
、![]() .若点C的横坐标为
.若点C的横坐标为![]() ,则四边形
,则四边形![]() 的面积为___________.
的面积为___________.
三、解答题(本大题共10小愿,共78分)
15. 解方程:
(1)![]()
(2)![]()
16. 已知关于x的一元二次方程![]() .
.
(1)若方程有实数根,求k的取值范围:
(2)若方程有两个相等的实数根,求方程的解.
17. 如图,在![]() 中,直径
中,直径![]() 与弦
与弦![]() 相交于点P,
相交于点P,![]() ,
,![]() .
.
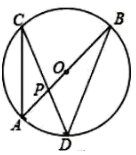
(1)求![]()
度数;
(2)若![]() ,求直径
,求直径![]() 的长.
的长.
18. 已知二次函数图象的顶点坐标是![]() ,且过点
,且过点![]() .
.
(1)求二次函数关系式;
(2)二次函数图象与y轴交点坐标是___________;
(3)当![]() 时,y的取值范围是___________.
时,y的取值范围是___________.
19. 在“美丽校园”建设中,某数学兴趣小组的同学想利用如图所示的直角墙角(两面墙体均足够长),用30米长的篱笆围成一个矩形花园![]() (篱笆只围
(篱笆只围![]() 、
、![]() 两边).在点
两边).在点![]() 处有一棵景观树,它与墙
处有一棵景观树,它与墙![]() 的距离为8米,与墙
的距离为8米,与墙![]() 的距离为16米,要求把这棵景观树围在花园内,且景观树与篱笆的距离不小于1米(不考虑树的粗细).设
的距离为16米,要求把这棵景观树围在花园内,且景观树与篱笆的距离不小于1米(不考虑树的粗细).设![]() 的长为
的长为![]() 米.
米.
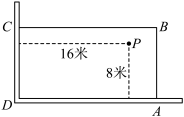
(1)求x的取值范围:
(2)若围成的矩形花园![]() 的面积为200平方米,求
的面积为200平方米,求![]() 的值.
的值.
20. 如图,AB是半圆O的直径,BD是一条弦,点C是![]() 的中点,
的中点,![]() 于点E,交BD于点F,连接AC、BC、CD.
于点E,交BD于点F,连接AC、BC、CD.
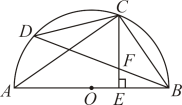
(1)求证:![]() ;
;
(2)若![]() ,
,![]() ,则
,则![]()
半径为___________.
21. 在平面直角坐标系中,抛物线![]() 与x轴交于点
与x轴交于点![]() 、
、![]() ,与y轴交于点C,直线
,与y轴交于点C,直线![]() 经过B、C两点.点D为线段BC上的一个动点,当点D不与B、C重合时,过点D作
经过B、C两点.点D为线段BC上的一个动点,当点D不与B、C重合时,过点D作![]() 轴,交抛物线于点E,过E作
轴,交抛物线于点E,过E作![]() 轴,交直线BC于点F.设点D的横坐标为m,线段EF的长为d.
轴,交直线BC于点F.设点D的横坐标为m,线段EF的长为d.
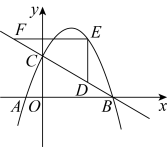
(1)直线BC所对应的函数关系式为___________,抛物线所对应的函数关系式为___________;
(2)求d与m的函数关系式,并直接写出自变量m的取值范围;
(3)求d最大值及此时点D的坐标.
22. 如图是某跳台滑雪训练场的横截面示意图,取某一位置的水平线为x轴,过跳台终点A作水平线的垂线为y轴,建立平面直角坐标系.图中的抛物线![]() 近似表示滑雪场地上的一座小山坡.某运动员从点O正上方7米处的点A滑出,滑出后沿一段抛物线:
近似表示滑雪场地上的一座小山坡.某运动员从点O正上方7米处的点A滑出,滑出后沿一段抛物线:![]() 运动.
运动.
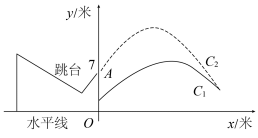
(1)当运动员运动到离A处的水平距离为4米时,离水平线的高度为10米,求抛物线![]() 的函数关系式(不要求写出自变量x的取值范围);
的函数关系式(不要求写出自变量x的取值范围);
(2)在(1)的条件下,当运动员运动的水平距离为多少米时,运动员与小山坡的竖直距离为1米?
(3)当运动员运动到坡顶正上方,且与坡顶距离超过3米时,求b的取值范围.
23. 在平面直角坐标系中,抛物线![]() (
(![]() 为常数)与
为常数)与![]() 轴交于点
轴交于点![]() ,过点
,过点![]() 作
作![]() 轴的平行线与抛物线交于点
轴的平行线与抛物线交于点![]() .
.
(1)点![]() 的坐标为___________.
的坐标为___________.
(2)若![]() ,求抛物线所对应
,求抛物线所对应函数关系式;
(3)当![]() 时,若抛物线
时,若抛物线![]() (
(![]() 为常数)的最低点到直线
为常数)的最低点到直线![]() 的距离为
的距离为![]() ,求
,求![]() 的值;
的值;
(4)已知点![]() ,
,![]() ,如果抛物线与线段
,如果抛物线与线段![]() 有且只有一个公共点,则
有且只有一个公共点,则![]() 的取值范围是___________.
的取值范围是___________.
2022-2023学年度吉林省长市师大附中明珠校区九年级上学期期中数学试题: 这是一份2022-2023学年度吉林省长市师大附中明珠校区九年级上学期期中数学试题,文件包含吉林省长市师大附中明珠校区九年级上学期期中数学试题原卷版docx、吉林省长市师大附中明珠校区九年级上学期期中数学试题解析版docx等2份试卷配套教学资源,其中试卷共36页, 欢迎下载使用。
2022-2023学年度吉林省长市南关区东北师大附中明珠学校九年级上学期起点分析数学试题: 这是一份2022-2023学年度吉林省长市南关区东北师大附中明珠学校九年级上学期起点分析数学试题,文件包含吉林省长市南关区东北师大附中明珠学校九年级上学期起点分析数学试题原卷版docx、吉林省长市南关区东北师大附中明珠学校九年级上学期起点分析数学试题解析版docx等2份试卷配套教学资源,其中试卷共31页, 欢迎下载使用。
2022-2023学年度吉林省长市南关区东北师大附中明珠学校九年级上学期期中数学试题: 这是一份2022-2023学年度吉林省长市南关区东北师大附中明珠学校九年级上学期期中数学试题,文件包含吉林省长市南关区东北师大附中明珠学校九年级上学期期中数学试题原卷版docx、吉林省长市南关区东北师大附中明珠学校九年级上学期期中数学试题解析版docx等2份试卷配套教学资源,其中试卷共33页, 欢迎下载使用。












