





2022-2023学年度吉林省长市吉林大学附属中学九年级上学期12月月考数学试题
展开数学试题
一、选择题(本大题共8小题,每小题3分,共24分)
1. 下列各式中,是![]() 关于
关于![]() 的二次函数的是( )
的二次函数的是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
2. 抛物线![]() 的顶点坐标为( )
的顶点坐标为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
3. 在![]() 中,
中,![]() ,
,![]() ,
,![]() ,那么
,那么![]()
值是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
4. 若![]() ,为二次函数
,为二次函数![]()
图像上的三点,则
![]() 的大小关系是( )
的大小关系是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
5. 已知抛物线![]() 如图所示,则下列结论中:①
如图所示,则下列结论中:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .说法正确的是( )
.说法正确的是( )
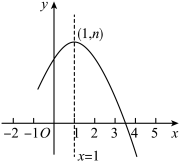
A. ①③④ B. ②③④ C. ①②③ D. ①②④
6. 如表中列出了二次函数y=ax2+bx+c的x、y的一些对应值,则一元二次方程ax2+bx+c=0的一个解x1的范围是( )
x | … | -3 | -2 | -1 | 0 | 1 | … |
y | … | -11 | -5 | -1 | 1 | 1 | … |
A. -3<x1<-2 B. -2<x1<-1 C. -1<x1<0 D. 0<x1<1.
7. 如图,在直角坐标系中,△OAB的顶点为O(0,0),A(4,3),B(3,0).以点O为位似中心,在第三象限内作与△OAB的位似比为![]() 的位似图形△OCD,则点C坐标( )
的位似图形△OCD,则点C坐标( )
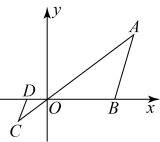
A. (﹣1,﹣1) B. (﹣![]() ,﹣1) C. (﹣1,﹣
,﹣1) C. (﹣1,﹣![]() ) D. (﹣2,﹣1)
) D. (﹣2,﹣1)
8. 如图,在平面直角坐标系中,矩形![]() 的顶点
的顶点![]() ,
,![]() 分别落在
分别落在![]() 轴、
轴、![]() 轴的正半轴上,
轴的正半轴上,![]() ,
,![]() ,若反比例函数
,若反比例函数![]() (k>0)经过
(k>0)经过![]() ,
,![]() 两点,则
两点,则![]() 的值为( )
的值为( )
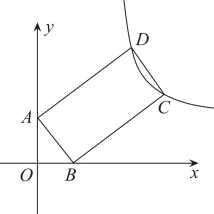
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
二、填空题(本大题共6小题,每小题3分,共18分)
9. 在下列二次函数中:①![]() ,②
,②![]() ,③
,③![]() ,图象开口最小的是________(填序号).
,图象开口最小的是________(填序号).
10. 已知二次函数![]() 的图像与x轴的一个交点为
的图像与x轴的一个交点为![]() ,则C的值是_______.
,则C的值是_______.
11. 将抛物线![]() 先向右平移1个单位长度,再向上平移2个单位长度,得到的新抛物线的函数表达式为________.
先向右平移1个单位长度,再向上平移2个单位长度,得到的新抛物线的函数表达式为________.
12. 四边形
![]() 中,
中,![]() ,
,![]() ,则
,则![]() ________.
________.
13. 汽车刹车后行驶的距离![]() (米)与行驶时间
(米)与行驶时间![]() (秒)的函数关系式是
(秒)的函数关系式是![]() .则汽车从刹车到停止所用时间为________秒.
.则汽车从刹车到停止所用时间为________秒.
14. 在平面直角坐标系中,抛物线![]() (
(![]() ,
,![]() 、
、![]() 为常数)的顶点为
为常数)的顶点为![]() ,与
,与![]() 轴交于点
轴交于点![]() ,点
,点![]() 关于抛物线对称轴的对称点为
关于抛物线对称轴的对称点为![]() .若
.若![]() 是等腰直角三角形,则
是等腰直角三角形,则![]() 的长为________.
的长为________.
三、解答题(共78分)
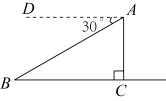
15. 如图,某飞机于空中![]() 处测得目标
处测得目标![]() ,此时垂直高度
,此时垂直高度![]() 米,从飞机上看到指挥所
米,从飞机上看到指挥所![]() 的俯角为
的俯角为![]() ,求飞机
,求飞机![]() 与指挥所
与指挥所![]() 之间的距离
之间的距离![]() 的长.
的长.
16. 用配方法将二次函数![]() 化成顶点式,并直接写出此二次函数的顶点坐标.
化成顶点式,并直接写出此二次函数的顶点坐标.
17. 某服装店购进单价为15元的童装若干件.销售一段时间后发现:当销售价为25元时平均每天能售出8件,而当售价每降低1元时,平均每天能多售出2件.当每件降价多少元时,该服装店平均每天的销售利润最大?最大利润是多少?
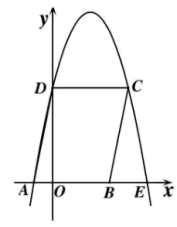
18. 如图,四边形![]() 是平行四边形,过点
是平行四边形,过点![]() 、
、![]() 、
、![]() 作抛物线
作抛物线![]() ,与
,与![]() 轴的另一交点为
轴的另一交点为![]() ,点
,点![]() 、
、![]() 、
、![]() 的坐标分别为
的坐标分别为![]() 、
、![]() 、
、![]() .求此抛物线的函数关系式.
.求此抛物线的函数关系式.
19. 图①、图②、图③均是![]() 的正方形网格,每个小正方形的顶点称为格点,线段
的正方形网格,每个小正方形的顶点称为格点,线段![]() 的端点和点
的端点和点![]() 均在格点上.请按要求完成作图,不写作法,保留作图痕迹.
均在格点上.请按要求完成作图,不写作法,保留作图痕迹.
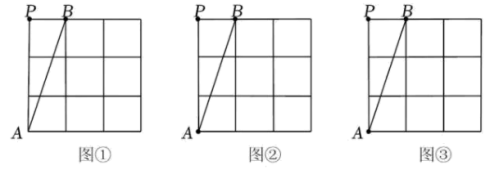
(1)在图①中的线段![]() 上确定一点
上确定一点![]() ,使
,使![]() ;
;
(2)在图②中的线段![]() 上确定一点
上确定一点![]() ,使
,使![]() ;
;
(3)在图③中的线段![]() 上确定一点
上确定一点![]() ,使
,使![]() .
.
20. 有一个抛物线形的拱形隧道,隧道的最大高度为![]() ,跨度为
,跨度为![]() .
.
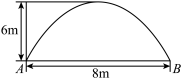
(1)请建立适当的平面直角坐标系,并求这条抛物线所对应的函数关系式;
(2)若要在隧道壁上左右对称地各安装一盏照明灯,灯离地面高![]() .求两灯之间的水平距离.
.求两灯之间的水平距离.
(3)隧道内设双向单车道(中间有一条隔离带,隔离带宽度忽略不计),一辆满载后车身宽![]() ,高
,高![]() 的卡车能否安全通过?
的卡车能否安全通过?
21. 如图,抛物线![]() 的顶点坐标为
的顶点坐标为![]() ,与
,与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() .直线
.直线![]() 的解析式为
的解析式为![]() .
.
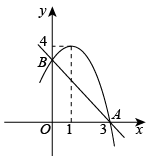
(1)求抛物线y1的解析式;
(2)当![]() 时,
时,![]() 的取值范围是 ___________;
的取值范围是 ___________;
(3)当![]() 的取值范围是 ___________时,
的取值范围是 ___________时,![]() 和
和![]() 都随着x的增大而减小;
都随着x的增大而减小;
(4)当![]() 时,
时,![]() 的取值范围是 ___________;
的取值范围是 ___________;
(5)当![]() 时,
时,![]() 的取值范围是 ___________.
的取值范围是 ___________.
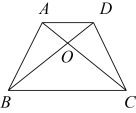
22. 【问题原型】如图①,在![]() 中,
中,![]() 是
是![]() 边的中线,
边的中线,![]() .
.
求证:![]() .
.
【结论应用】如图②,在![]() 中,
中,![]() 为锐角,
为锐角,![]() 为
为![]() 中点,连结
中点,连结![]() ,将四边形
,将四边形![]() 沿
沿![]() 折叠,得到四边形
折叠,得到四边形![]() ,点
,点![]() 、
、![]() 的对应点分别为点
的对应点分别为点![]() 、
、![]() .
.
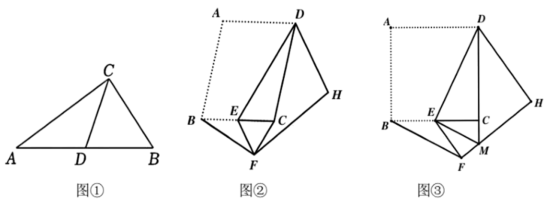
(1)![]() 与
与![]()
位置关系是________;
(2)连结![]() ,若
,若![]() ,求
,求![]() 的度数;
的度数;
(3)如图③,当![]() 为边长为4的正方形时,其余条件不变,延长
为边长为4的正方形时,其余条件不变,延长![]() 交
交![]() 于点
于点![]() ,连结
,连结![]() ,直接写出线段
,直接写出线段![]() 的长.
的长.
23. 如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() .点
.点![]() 从点
从点![]() 出发,沿折线
出发,沿折线![]() 运动,在
运动,在![]() 上以每秒5个单位
上以每秒5个单位速度运动,在
![]() 上以每秒2个单位的速度运动.点
上以每秒2个单位的速度运动.点![]() 从点
从点![]() 出发,以每秒
出发,以每秒![]() 个单位的速度向点
个单位的速度向点![]() 运动.两个点同时出发,其中一个点到达终点时,另一个点也随之停止运动.过点
运动.两个点同时出发,其中一个点到达终点时,另一个点也随之停止运动.过点![]() 作
作![]() 于点
于点![]() ,连结
,连结![]() ,以
,以![]() 、
、![]() 为边作
为边作![]() .设点
.设点![]() 的运动时间
的运动时间![]() (秒).
(秒).
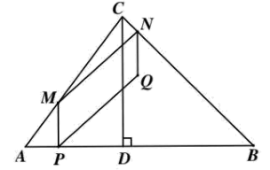
(1)线段![]() 的长为________;
的长为________;
(2)用含有![]() 的代数式表示
的代数式表示![]() 的长;
的长;
(3)当点![]() 在
在![]() 上运动时,若
上运动时,若![]() 是轴对称图形,求
是轴对称图形,求![]() 的值;
的值;
(4)设点![]() 是点
是点![]() 关于
关于![]() 的对称点.当点
的对称点.当点![]() 在
在![]() 上运动时,连结
上运动时,连结![]() ,当
,当![]() 时,直接写出
时,直接写出![]() 的值.
的值.
24. 已知抛物线![]() 的对称轴为直线
的对称轴为直线![]() ,且过点
,且过点![]() .直线
.直线![]() 与抛物线交于
与抛物线交于![]() 、
、![]() 两点,且点
两点,且点![]() 在点
在点![]() 的左侧.
的左侧.
(1)求此抛物线的解析式;
(2)求线段![]() 的长;
的长;
(3)点![]() 是抛物线上一点,其横坐标为
是抛物线上一点,其横坐标为![]() ,且
,且![]() .抛物线在
.抛物线在![]() 、
、![]() 两点之间的部分(包括
两点之间的部分(包括![]() 、
、![]() 两点)记为图象
两点)记为图象![]() .当图象
.当图象![]() 上的最高点与最低点到直线
上的最高点与最低点到直线![]() 的距离相等时,求
的距离相等时,求![]() 的值;
的值;
(4)点![]() 在抛物线上,点
在抛物线上,点![]() 在其对称轴上.当以
在其对称轴上.当以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是平行四边形时,请直接写出点
为顶点的四边形是平行四边形时,请直接写出点![]() 的坐标.
的坐标.
吉林省长春市朝阳区吉林大学附属中学2023-2024学年九年级上学期期末数学试题(无答案): 这是一份吉林省长春市朝阳区吉林大学附属中学2023-2024学年九年级上学期期末数学试题(无答案),共5页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
吉林省长春市朝阳区吉林大学附属中学2023-2024学年九年级上学期期中数学试题(无答案): 这是一份吉林省长春市朝阳区吉林大学附属中学2023-2024学年九年级上学期期中数学试题(无答案),共6页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
吉林省长春市吉林大学附属中学2023-2024学年九年级上学期第一次月考数学试题(无答案): 这是一份吉林省长春市吉林大学附属中学2023-2024学年九年级上学期第一次月考数学试题(无答案),共6页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。












