





2022-2023学年度吉林省长市第二实验学校九年级上学期10月月考数学试题
展开吉林省第二实验学校2022—2023学年度上学期九年级第二次月考
数学试题(三年制)
一、选择题(本大题共8小题,每小题3分,共24分)
1. ![]() 的绝对值是( )
的绝对值是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
2. 党的十八大以来,以习近平同志为核心的党中央重视技能人才的培育与发展.据报道,截至2021年底,我国高技能人才超过65000000人,将数据65000000用科学记数法表示为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
3. 如图是由5个相同的正方体搭成的几何体,这个几何体的俯视图是( )
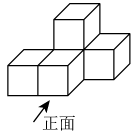
A.  B.
B. 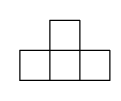
C.  D.
D. 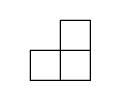
4. 二次函数![]() ,下列说法正确的是( )
,下列说法正确的是( )
A. 开口向下 B. 对称轴为直线![]()
C. 顶点坐标为![]() D. 当
D. 当![]() 时,y随x的增大而减小
时,y随x的增大而减小
5. 把一块直尺与一块三角板如图放置,若![]() ,则
,则![]() 的度数为( )
的度数为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
6. 如图,小明在点C处测得树的顶端A仰角为α,同时测得AC=15m,则树的高度AB为( )m.

A. 15sinα B. ![]() C. 15tanα D.
C. 15tanα D. ![]()
7. 在△ABC中,∠ACB=90°,用直尺和圆规在AB上确定点D,使△ACD∽△CBD,根据作图痕迹判断,正确是( )
A.  B.
B.  C.
C.  D.
D. 
8. 如图,菱形OABC在第一象限内,∠AOC=45°,反比例函数![]() 的图象经过点A,交BC边于点D,若△AOD的面积为
的图象经过点A,交BC边于点D,若△AOD的面积为![]() ,则k的值为( )
,则k的值为( )

A. ![]() B.
B. ![]() C. 3 D. 2
C. 3 D. 2
二、填空题(本大题共6小题,每小题3分,共18分)
9. 分解因式:![]() _____.
_____.
10. 在实数0,![]() ,
,![]() ,
,![]() 中,最小的数是______.
中,最小的数是______.
11. 若关于x的一元二次方程![]() 有实数根,则k的取值范围是 _____.
有实数根,则k的取值范围是 _____.
12. 如图,在平面直角坐标系中,![]() 和
和![]() 是以坐标原点O为位似中心的位似图形,点B、
是以坐标原点O为位似中心的位似图形,点B、![]() 的坐标分别为
的坐标分别为![]() 、
、![]() 若点A的坐标为
若点A的坐标为![]() ,则点
,则点![]() 的坐标为 _____.
的坐标为 _____.

13. 如图,在矩形ABCD中,AD=3,CD=4,点P是AC上一个动点(点P与点A,C不重合),过点P分别作PE⊥BC于点E,PF∥BC交AB于点F,连接EF,则EF的最小值为_____.

14. 如图,在平面直角坐标系中,点![]() 在抛物线
在抛物线![]() 上,过点A作y轴
上,过点A作y轴垂线,交抛物线于另一点B,点C、D在线段AB上,分别过点C、D作x轴的垂线交抛物线于E、F两点.当四边形CDFE为正方形时,线段CD的长为_________.

三、解答题(共78分)
15. 先化简,再求值:![]() ,其中
,其中![]() .
.
16. 某社区组织A,B,C,D四个小区的居民进行核酸检测,有很多志愿者参与此项检测工作,志愿者王明和李丽分别被随机安排到这四个小区中的一个小区组织居民排队等候.
(1)王明被安排到A小区进行服务的概率是 .
(2)请用列表法或画树状图法求出王明和李丽被安排到同一个小区工作的概率.
17. 已知抛物线![]() 经过
经过![]() 、
、![]() 两点.
两点.
(1)请求出抛物线的解析式;
(2)当![]() 时,请直接写出y的取值范围.
时,请直接写出y的取值范围.
18. 图①、图②、图③均是![]()
正方形网格,每个小正方形的顶点称为格点,线段AB、BC的端点均在格点上,只用无刻度的直尺,在给定的网格中按下列要求以AB、BC为邻边画四边形,使第四个顶点在格点上.
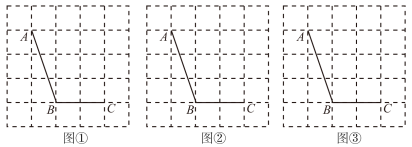
(1)在图①中画一个中心对称的四边形ABCD.
(2)在图②中画一个轴对称的四边形ABCE.
(3)在图③中画一个非轴对称的四边形ABCF,且使![]() .
.
19. 如图,在平行四边形ABCD中,连接BD,E为线段AD的中点,延长BE与CD的延长线交于点F,连接AF,∠BDF=90°
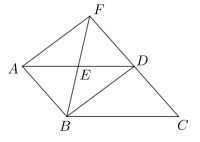
(1)求证:四边形ABDF是矩形;
(2)若AD=5,DF=3,求四边形ABCF的面积S.
20. 2022年3月23日,神舟十三号3名航天员在中国空间站为青少年们讲授了“天宫课堂”第二课,点燃了无数青少年心中的科学梦想.海豚学校4月份组织了首届“航天梦 报国情”航天知识竞赛,八年级全体学生参加了“航天知识竞赛”,为了解本次竞赛的成绩,小军随机抽取八年级20名参赛学生的成绩(单位:分).
收集数据:
90,75,80,80,70,75,80,85,82,95,95,75,90,70,92,95,84,75,85,67
整理数据:
成绩x/分 |
|
|
|
|
频数 | 1 | 6 | a | b |
分析数据:
平均数 | 中位数 | 众数 |
82 | c | d |
根据上述数据回答以下问题:
(1)请直接写出表格中a,b,c,d的值:
(2)活动组委会决定,给成绩在90分及以上的同学授予“小宇航员”称号.根据上面的统计结果,估计该校八年级1000人中约有多少人将获得“小宇航员”称号;
(3)样本20名参赛学生中的小蕾同学成绩为83分,请你从平均数、中位数中选择一个统计量来说说小蕾的成绩如何?
21. 甲、乙两人在净月大街上同起点、同终点、同方向匀速步行2400米,先到终点的人原地休息.已知甲先出发4分钟,在整个步行过程中,甲、乙两人间的距离y(米)与甲出发的时间x(分)之间的关系如图中折线OA﹣AB﹣BC﹣CD所示.
(1)甲速度为 米/分,乙的速度为 米/分.
(2)求线段AB的表达式,并写出自变量x的取值范围.
(3)求乙比甲早几分钟到达终点?

22. [感知]如图①所示,在等腰![]() 中,
中,![]() ,AD平分
,AD平分![]() ,易得
,易得![]() (不需要证明)
(不需要证明)
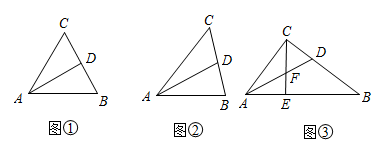
(1)[探究]如图②所示,李丽同学将图①的等腰![]() 改为任意
改为任意![]() ,AD平分
,AD平分![]() ,他通过观察、测量,猜想
,他通过观察、测量,猜想![]() 仍然成立,为了证明自己的猜想,他与同学进行交流讨论,得到了证明猜想的两种方法:
仍然成立,为了证明自己的猜想,他与同学进行交流讨论,得到了证明猜想的两种方法:
方法1:过点D分别作![]() 于点E,
于点E,![]() 于点F,利用
于点F,利用![]() 与
与![]()
面积比证明结论.
方法2:过点B作![]() 交AD延长线于点E,利用
交AD延长线于点E,利用![]() 与
与![]() 相似证明结论.
相似证明结论.
请你参考上面的两种方法,选择其中的一种方法完成证明.
(2)[应用]如图③所示,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,AD平分
,AD平分![]() .若点E在边AB上,
.若点E在边AB上,![]() ,CE交AD于点F,则
,CE交AD于点F,则![]() ______.
______.
23. 如图,在平面直角坐标系中,已知抛物线![]() 的顶点为
的顶点为![]() ,与
,与![]() 轴交于点
轴交于点![]() ,线段
,线段![]() 轴,交该抛物线于另一点
轴,交该抛物线于另一点![]() .
.

(1)抛物线对称轴是直线______;
(2)求点![]() 的坐标;
的坐标;
(3)点![]() 为抛物线上一点,若
为抛物线上一点,若![]() ,求点
,求点![]() 的坐标;
的坐标;
(4)平移抛物线![]() ,使其顶点始终在直线
,使其顶点始终在直线![]() 上移动,当平移后的抛物线与射线
上移动,当平移后的抛物线与射线![]() 只有一个公共点时,设此时抛物线的顶点横坐标为
只有一个公共点时,设此时抛物线的顶点横坐标为![]() ,请直接写出
,请直接写出![]() 的取值范围.
的取值范围.
24. 如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,O是边
,O是边![]() 的中点,动点P从点C出发以每秒1个单位的速度沿折线
的中点,动点P从点C出发以每秒1个单位的速度沿折线![]() 向终点A运动(不与
向终点A运动(不与![]() 顶点重合),点P在运动的过程中,线段
顶点重合),点P在运动的过程中,线段![]() 将
将![]() 分成两部分,将所得三角形部分沿
分成两部分,将所得三角形部分沿![]() 折叠得到
折叠得到![]() ,设
,设![]() 与
与![]() 重叠部分面积为S,点P运动时间是t(秒).
重叠部分面积为S,点P运动时间是t(秒).

(1)用含t的代数式表示![]() ;
;
(2)当点E落到![]() 边上时,求t值;
边上时,求t值;
(3)当点P在![]() 边上且
边上且![]() 所在直线把
所在直线把![]() 面积分成1:3两部分时,求S的值;
面积分成1:3两部分时,求S的值;
(4)当点P在![]() 边上且
边上且![]() 所在直线与
所在直线与![]() 边所夹锐角等于
边所夹锐角等于![]() 时,直接写出此时t的值.
时,直接写出此时t的值.
2022-2023学年度吉林省长市长高新第二实验学校九年级上学期第三次月考数学试题: 这是一份2022-2023学年度吉林省长市长高新第二实验学校九年级上学期第三次月考数学试题,文件包含吉林省长市长高新第二实验学校九年级上学期第三次月考数学试题原卷版docx、吉林省长市长高新第二实验学校九年级上学期第三次月考数学试题解析版docx等2份试卷配套教学资源,其中试卷共33页, 欢迎下载使用。
2022-2023学年度吉林省长市南关区第二实验中学九年级上学期8月月考数学试题: 这是一份2022-2023学年度吉林省长市南关区第二实验中学九年级上学期8月月考数学试题,文件包含吉林省长市南关区第二实验中学九年级上学期8月月考数学试题原卷版docx、吉林省长市南关区第二实验中学九年级上学期8月月考数学试题解析版docx等2份试卷配套教学资源,其中试卷共39页, 欢迎下载使用。
2022-2023学年度吉林省长市吉林大学附属中学九年级上学期12月月考数学试题: 这是一份2022-2023学年度吉林省长市吉林大学附属中学九年级上学期12月月考数学试题,文件包含吉林省长市吉林大学附属中学九年级上学期12月月考数学试题原卷版docx、吉林省长市吉林大学附属中学九年级上学期12月月考数学试题解析版docx等2份试卷配套教学资源,其中试卷共36页, 欢迎下载使用。












