2022-2023学年度吉林省长市南关区东北师大附中明珠学校九年级上学期期中数学试题

这是一份2022-2023学年度吉林省长市南关区东北师大附中明珠学校九年级上学期期中数学试题，文件包含吉林省长市南关区东北师大附中明珠学校九年级上学期期中数学试题原卷版docx、吉林省长市南关区东北师大附中明珠学校九年级上学期期中数学试题解析版docx等2份试卷配套教学资源，其中试卷共33页， 欢迎下载使用。

吉林省长春市南关区东北师大附中明珠校区2022-2023学年九年级（上）期中数学试卷
一、选择题（本大题共8小题，每小题3分，共24分）
1. 下列函数属于二次函数的是（　　）
A. B.
C. D.
【答案】D
【解析】
【分析】根据二次函数的定义：形如，则是的二次函数，从而可得答案．
【详解】解：A．不是整式，故A错误；
B．整理后得到，是一次函数，故B错误
C．，当时，是一次函数，故C错误；
D．是二次函数的顶点式解析式，故D正确．
故选：D．
【点睛】本题考查的是二次函数的定义，掌握二次根式的定义是解题的关键．
2. 如图所示，A、B、C、D是⊙O上的点，，下列结论错误的是（　　）

A. B. C. D.
【答案】C
【解析】
【分析】由A、B、C、D是⊙O上的点，，根据在同圆或等圆中，如果两个圆心角，两个圆周角，两条弧，两条弦，两条弦心距中有一组量相等，那么它们所对应的其余各组量都分别相等作答即可．
【详解】，
，，故A选项正确；
，即，故B选项正确；
，
，故D选项正确；
不能证明，故C选项错误；
故选：C．
【点睛】本题考查了圆心角，弦，弧之间的关系，熟练掌握知识点是解题的关键．
3. 点都在二次函数的图象上，则的大小关系为（　　）
A. B. C. D.
【答案】A
【解析】
【分析】由二次函数解析式可得函数对称轴和增减性，再根据离对称轴的远近的点的纵坐标的大小比较，即可得出的大小关系．
【详解】解：二次函数的图象开口向下，对称轴为直线，在对称轴左侧，y随x的增大而增大，
∴关于对称轴的对称点为，
∵，
∴，
故选：A．
【点睛】本题考查比较函数值的大小．解决此题的关键是理解当二次函数开口向下时，在函数图象上距离对称轴越远的点，函数值越小；当二次函数开口向上时，在函数图象上距离对称轴越远的点，函数值越大．
4. 用直角钢尺检查某一工件是否恰好是半圆环形，在下面四种情形中，可判断工件是半圆环形的（ ）
A. B.
C. D.
【答案】B
【解析】
【分析】由半圆（或直径）所对的圆周角是直角，的圆周角所对的弦是直径，即可得出答案．
【详解】解：∵的圆周角所对的弦是直径，
∴B选项是半圆环形．
故选B．
【点睛】此题考查了圆周角定理，熟记的圆周角所对的弦为直径是解题的关键．
5. 已知抛物线过点，则该抛物线的对称轴为（　　）
A. 直线 B. 直线 C. 直线 D. 直线
【答案】C
【解析】
【分析】根据抛物线的对称性，利用两点的函数值相同，两点关于对称轴对称进行求解即可．
【详解】解：∵，
∴两点关于对称轴对称，
∴对称轴为：；
故选C．
【点睛】本题考查二次函数的对称轴．熟练掌握函数值相同的两点关于对称轴对称是解题的关键．
6. 将抛物线向左平移2个单位长度，再向下平移3个单位长度，得到的抛物线的解析式为（ ）
A. B. C. D.
【答案】A
【解析】
【分析】根据抛物线平移变化规律左加右减，上加下减求解即可．
【详解】解：抛物线向左平移2个单位长度，再向下平移3个单位长度，得到的抛物线的解析式为，即，
故选：A．
【点睛】本题考查了抛物线的平移，解题关键是明确平移变化规律左加右减自变量，上加下减常数项．
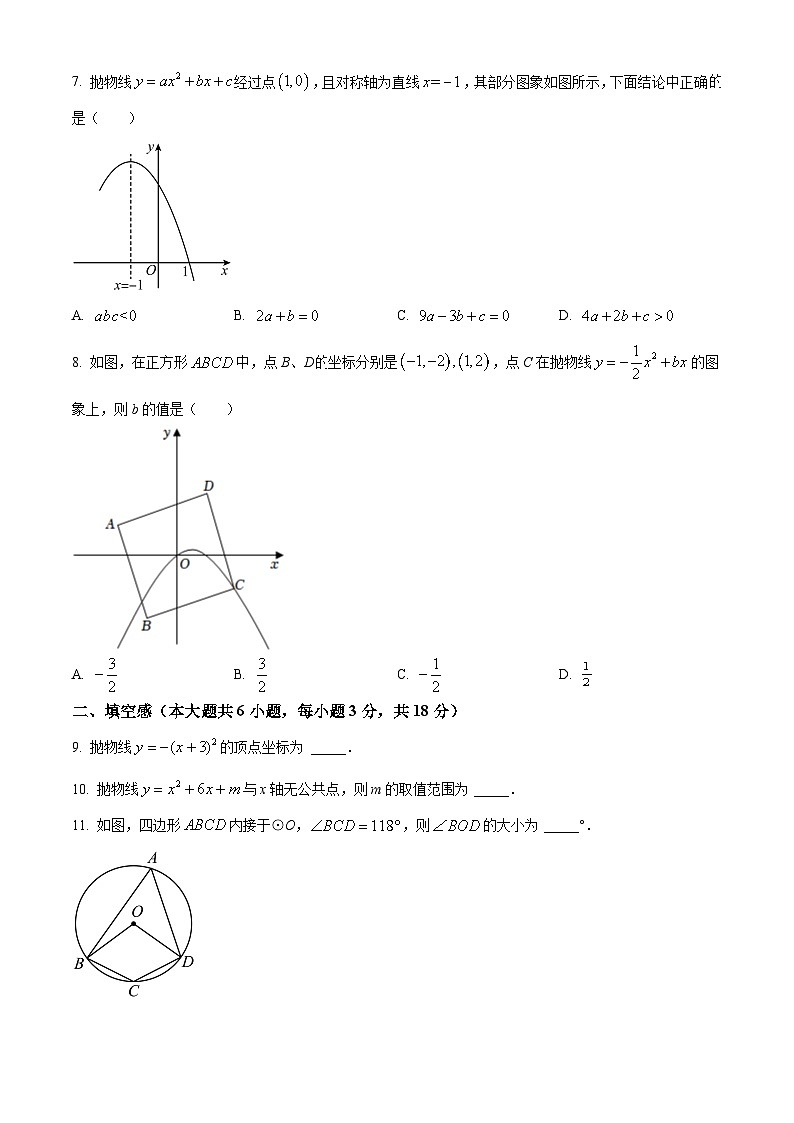
7. 抛物线经过点，且对称轴为直线，其部分图象如图所示，下面结论中正确的是（　　）

A. B. C. D.
【答案】C
【解析】
【分析】根据二次函数的图象和性质，逐一进行判断即可．
【详解】解：由图象可知：
抛物线开口向下，
∴，
对称轴为：，
∴，
与轴交于正半轴，
∴，
过点：，
∴，
根据对称性，图象过，
∴；
A、，选项错误，不符合题意；
B、，选项错误，不符合题意；
C、，选项正确，符合题意；
D、，选项错误，不符合题意；
故选C．
【点睛】本题考查根据二次函数的图象，判断系数的符号以及式子的符号．根据图象准确的获取信息，熟练掌握二次函数的性质，是解题的关键．
8. 如图，在正方形中，点B、D的坐标分别是，点C在抛物线的图象上，则b的值是（　　）

A. B. C. D.
【答案】D
【解析】
【分析】连接OB、OC，过点B作轴于点M，过点C作轴于点N，由正方形的性质可证明，由全等三角形的性质可求点C的坐标，将点C的坐标代入抛物线解析式即可求解．
【详解】连接OB、OC，过点B作轴于点M，过点C作轴于点N，

，
在正方形中，点B、D的坐标分别是，
∴点O为正方形对角线的交点，
∴，
，
，
，
，
，
∵点C在抛物线的图象上，
，
解得，
故选：D．
【点睛】本题考查了正方形的性质，全等三角形的判定和性质，求二次函数解析式，熟练掌握知识点是解题的关键．
二、填空感（本大题共6小题，每小题3分，共18分）
9. 抛物线的顶点坐标为 _____．
【答案】
【解析】
【分析】根据二次函数顶点式顶点坐标：，直接进行作答即可．
【详解】解：的顶点坐标为：；
故答案为：．
【点睛】本题考查二次函数顶点式的顶点坐标．熟记顶点式的顶点坐标为：是解题的关键．
10. 抛物线与x轴无公共点，则m的取值范围为 _____．
【答案】
【解析】
【分析】抛物线与x轴无公共点，也就是方程无实数根，根据根的判别式列式求解即可．
【详解】解：∵抛物线与x轴无公共点，
∴方程无实数根，
∴，
∴，
故答案为：．
【点睛】本题考查了抛物线与x轴的交点与一元二次方程根的关系；熟记抛物线与x轴的交点个数和一元二次方程根的关系是解决问题的关键．当二次函数与x轴有一个交点时，则对应的一元二次方程有两个相等的实数根；当二次函数与x轴有两个交点时，则对应的一元二次方程有两个不相等的实数根；当二次函数与x轴没有交点时，则对应的一元二次方程没有实数根．
11. 如图，四边形内接于⊙O，，则的大小为 _____°．

【答案】##124度
【解析】
【分析】根据圆内接四边形的对角互补求出的度数，再根据同弧所对的圆心角是圆周角的2倍，求解即可．
【详解】∵四边形内接于⊙O，
，
，
，
，
故答案为：．
【点睛】本题考查了圆内接四边形的对角互补，同弧所对的圆心角是圆周角的2倍，数来能掌握知识点是解题的关键．
12. 某种礼炮的升空高度h（m）与飞行时间t（s）的关系式是，则这种礼炮从点火升空到最高点引爆需要的时间为 _____s．
【答案】6
【解析】
【分析】把二次函数的一般式写成顶点式，找出顶点坐标，即可知道多长时间后得到最高点．
【详解】解：
，
∵，
∴这个二次函数图象开口向下．
∴当时，升到最高点．
故答案为：6．
【点睛】本题考查二次函数的应用，解题的关键是熟练掌握二次函数的性质．
13. 已知抛物线经过点，则不等式的解集是 _____．
【答案】或
【解析】
【分析】根据抛物线经过点，可得抛物线开口向下，且当时，或，再根据二次函数的图象和性质即可得出答案．
【详解】解：∵抛物线经过点，
抛物线开口向下，且当时，或，
不等式的解集是或，
故答案为：或．
【点睛】本题考查了利用二次函数的图象解一元二次不等式，熟练掌握知识点并运用数形结合的思想是解题的关键．
14. 在平面直角坐标系中，抛物线与y轴交于点A，过点A作x轴平行线交抛物线于点B，若点B关于的对称点C恰好落在抛物线上，则a值为_____．
【答案】##
【解析】
【分析】先根据二次函数的性质及题意求出点B的坐标，再根据对称的性质求出点C的坐标，最后将点C的坐标代入二次函数解析式求解即可．
【详解】当时，，∴点A的坐标为，
∵抛物线的对称轴为，过点A作x轴平行线交抛物线于点B，
，
设点B关于的对称点C的坐标为，
则有，解得，
∴，
∵点C恰好落在抛物线上，
，
解得，
故答案：．
【点睛】本题考查了二次函数的性质，关于某点对称的点的坐标，熟练掌握知识点并能够综合运用是解题的关键．
三、解答题（本大题共10小题，共78分）
15. 将二次函数配方成的形式，结果为______，顶点坐标为______．
【答案】，
【解析】
【分析】先将二次根式的一般式化为顶点式，再根据二次函数顶点式的表示方法表示即可．
【详解】，
∴顶点坐标为，
故答案为：．
【点睛】本题考查二次函数的顶点式，熟练掌握知识点是解题的关键．
16. 圆形拱门屏风是中国古代家庭中常见的装饰隔断，既美观又实用，彰显出中国元素的韵味，如图，是一款拱门的示意图，其中拱门最下端分米，为的中点，为拱门最高点，圆心在线段上，分米，求拱门所在圆的半径．

【答案】15分米
【解析】
【分析】连接，根据垂径定理求得，设圆的半径为分米，则，根据勾股定理即可求得．
【详解】解：连接，

∵过圆心，为的中点，
∴，
∵为的中点，
∴，
设圆的半径为x分米，则分米，
∵，
∴，
在中，，
∴，
∴（分米），
即拱门所在圆的半径是15分米．
【点睛】本题主要考查了垂径定理的应用，勾股定理，能够准确作出辅助线，根据勾股定理列出方程是解决问题的关键．
17. 已知二次函数．
（1）当时，求y的取值范围．
（2）当时，x的取值范围是______．
【答案】（1）
（2）
【解析】
【分析】（1）先将一般式化为顶点式，判断出抛物线的对称轴和开口方向，再根据二次函数的性质进行求解即可；
（2）先通过解方程求出或时函数值为3，再根据抛物线开口向下，且对称轴为直线求解即可．
【小问1详解】
解：，
对称轴为直线，
∵，
∴抛物线开口向下，
∴当时，随的增大而减小，
当时，；当时，；
∴y的取值范围为；
【小问2详解】
解：当时，
解得：或，
∵抛物线开口向下，且对称轴为直线，
∴当时，x的取值范围是，
故答案为：．
【点睛】本题考查了二次函数的图象和性质，解一元二次方程，将二次函数一般式化为顶点式，熟练掌握知识点是解题的关键．
18. 如图，四边形内接于，是直径，且平分，连结．

（1）试判断形状，并给出证明．
（2）若，则______，长度为______．
【答案】（1）等腰直角三角形；证明见解析
（2）30，6
【解析】
【分析】（1）根据直径所对的角是，以及等角，等弧，等弦，即可得证；
（2）根据圆周角定理，求出度数即可；延长交于点，连接，利用圆周角定理和的直角三角形进行求解即可．
【小问1详解】
是等腰直角三角形，证明如下：
∵是直径，
∴，
∵平分，
∴，
∴，
∴，
∴是等腰直角三角形；
【小问2详解】
解：∵是等腰直角三角形，
∴，
∵，
∴，
∵，
∴；
延长交于点，连接，

则：，，
∴，
∴．
故答案为：30，6．
【点睛】本题考查圆周角定理．熟练掌握直径所对的圆周角是，以及同弧所对圆周角相等是解题的关键．
19. 小明进行实心球训练，他尝试利用数学模型来研究实心球的运动情况，建立了如图所示的平面直角坐标系，实心球从y轴上的点A处出手，运动路径可看作抛物线，在点B处达到最高位置，落在x轴上的点C处．小明某次试投时的数据如图所示．

（1）根据图中信息，求出实心球路径所在抛物线的表达式．
（2）若实心球投掷距离（实心球落地点C与出手点A的水平距离OC的长度）不小于9.6m，成绩为满分，请通过计算，判断小明此次试投的成绩是否能达到满分．
【答案】（1）
（2）小明此次试投的成绩能达到满分，理由见解析
【解析】
【分析】（1）由题意得，抛物线的顶点坐标为，点A的坐标为，设抛物线解析式为，利用待定系数法代入求解即可；
（2）令，即，解方程求解即可得出结论．
【小问1详解】
由题意得，抛物线的顶点坐标为，点A的坐标为，
设抛物线解析式为，
∵抛物线经过点A，
，
解得，
∴抛物线解析式为；
【小问2详解】
令，即，
解得或（舍去），
，
，
所以，小明此次试投的成绩能达到满分．
【点睛】本题考查了二次函数在实际问题中的应用，正确理解题意，熟练掌握待定系数法及二次函数与一元二次方程的关系是解题的关键．
20. 如图，直线分别交x轴、y轴于A、B两点，抛物线过点A、B．

（1）求抛物线解析式．
（2）点M是抛物线上的一点，且在直线上方，连结．设点M横坐标为m，的面积为S，求S与m之间的函数关系式，并直接写出自变量m的取值范围．
【答案】（1）
（2）
【解析】
【分析】（1）先求出A、B两点的坐标，再利用待定系数法直接求解即可；
（2）由题意得，过点M作轴，交于点N，表示出点N的坐标为，求出MN的长度，再根据，代入求解即可．
【小问1详解】
当时，，，
当时，，，
把A、B两点的坐标代入，得，
解得，
∴抛物线解析式为；
【小问2详解】
由题意得，
过点M作轴，交于点N，

∴点N的坐标为，
，
∵，
，
．
【点睛】本题考查了二次函数图象与x轴的交点坐标，待定系数法求二次函数解析式，二次函数与几何图形的面积问题，熟练掌握知识点是解题的关键．
21. 在学习函数时，我们通过“列表、描点、连线”的方法画函数图象，并结合图象研究函数的性质．运用此方法研究函数的图象与性质．
[操作画图]
①请完成以下列表：
x
…




0

1

2
…
y
…
2
a


0
b


2
…
则______， ______．
②在平面直角坐标系中画出的图象．

[观察发现]
③观察函数图象，写出关于这个函数的两条性质．
[拓展应用]
④若关于x的方程有两个不相等的实数根，则m的取值范围是______．
【答案】①；②见解析；③函数图象关于轴对称；函数有最小值；④或
【解析】
【分析】①将，代入函数解析式，求解即可；
②根据①中的表格描点、连线即可；
③观察图象即可得出答案；
④方程解为函数和图象的交点，根据图象即可求解．
【详解】解：①当时，；
当时，；
故答案为：；
②图象如下：

③观察图象可得：函数图象关于轴对称；函数有最小值；
④方程的解为函数和图象的交点，
由图象可得，当或时，函数和图象有两个交点，


即方程有两个不相等的实数根，
当时，
当与有1个交点时，有三个实数根，
此时，即，

解得
结合图象可知，或，
故答案为：或．
【点睛】本题考查了二次函数的图象和性质，准确理解题意，熟练掌握知识点是解题的关键．
22. 金秋十月，我省某农业合作社有机水稻再获丰收，加工成有机大米后通过实体和电商两种渠道进行销售．该有机大米成本为每千克12元，销售价格不低于成本，且不超过22元/千克，根据各销售渠道的反馈，发现该有机大米一天的销售量y（千克）是该天的售价x（元/千克）的一次函数，部分情况如表：
售价x（元/千克）
…
14
16
18
…
销售量y（千克）
…
800
700
600
…

（1）求一天的销售量y（千克）与售价x（元/千克）之间的函数关系式，并写出x的取值范围．
（2）若某天销售这种大米获利3250元，那么这天该大米的售价为多少？
（3）该有机大米售价定为多少时，当天获利最大？最大利润为多少？
【答案】（1）
（2）17元 （3）4050元
【解析】
【分析】（1）用待定系数法求函数解析式即可；
（2）根据“利润=售价-成本，获利=利润×销量”列方程求解即可；
（3）先列出获利w与售价的函数关系式，然后再根据二次函数的性质求最值即可．
【小问1详解】
解：设一天的销售量y（千克）与售价x（元/千克）之间的函数关系式为
由题意得：，解得：
所以一天的销售量y（千克）与售价x（元/千克）之间的函数关系式为．
【小问2详解】
解：设这天该大米的售价为元
由题意可得：
解得或（舍）．
∴这天该大米的售价为17元．
【小问3详解】
解：由题意可得：有机大米一天的获利w（元）与该天的售价x（元/千克）的函数关系式为：
∴当时，y随x的增大而增大．
∴当时，w有最大值4050元．
【点睛】本题主要考查了二次函数的应用、求一次函数解析式、一元二次方程的应用等知识点，正确求得一天的销售量y（千克）与售价x（元/千克）之间的函数关系式是解答本题的关键．
23. 如图，在平面直角坐标系中，抛物线（b、c为常数）的顶点坐标为，与x轴交于A、B两点（点A在点B左侧），与y轴交于点C，点C，点D关于x轴对称，连结，作直线．

（1）求b、c的值；
（2）求点A、B的坐标；
（3）求证：；
（4）点P在抛物线上，点Q在直线BD上，当以点C、D、P、Q为顶点的四边形为平行四边形时，直接写出点Q的坐标．
【答案】（1）
（2）
（3）见解析 （4）或或或
【解析】
【分析】（1）直接利用待定系数法求二次函数解析式即可求解；
（2）令，代入函数解析式，解一元二次方程即可求解；
（3）先求出D点坐标，分别表示出的长度，再求解的正切值相等即可得到角相等；
（4）当为平行四边形的对角线时，由中点坐标公式列出方程组，进而求解；当、是平行四边形的对角线时，同理可解．
【小问1详解】
∵抛物线（b、c为常数）的顶点坐标为，
，
；
【小问2详解】
当时，或，
∵点A在点B左侧，
；
【小问3详解】
，点C，点D关于x轴对称，
，
，
，
，
，
，
，
；
小问4详解】
设直线的解析式为，
把B、D的坐标代入解析式，得，
解得，
∴直线的解析式为，
∴设点，点，，
当为平行四边形的对角线时，由中点坐标公式得：
，
整理得：，解得：（舍去）或2，
则，即点；
当是平行四边形的对角线时，同理可得：
，解得：，
即点；
当是平行四边形的对角线时，同理可得：
，解得：，
即点的坐标为或，
综上，点的坐标为：或或或．
【点睛】本题考查了待定系数法求二次函数解析式和一次函数解析式，二次函数中平行四边形存在性问题和二次函数图象与x轴的交点问题，正切，熟练掌握知识点是解题的关键．
24. 记函数的图象为，函数的图象记为，图象和记为图象G．
（1）若点在图象G上，求m的值．
（2）已知直线l与x轴平行，且与图象G有三个交点，从左至右依次为点A、点B、点C，若，求点C坐标．
（3）若当时，，直接写出n的取值范围．
（4）点P坐标为，过点P作x轴、y轴垂线，垂足分别为点M、点N，当矩形与图象G有两个公共点时，直接写出t的取值范围．
【答案】（1）
（2）
（3）
（4）或
【解析】
【分析】（1）根据可判断出点在图象上，将坐标代入解析式，求解即可；
（2）由图象可知，直线l与x轴平行，且与图象G有三个交点时，，设直线l解析式为，联立，整理得，结合，利用两点间距离公式，再根据根与系数的关系进行求解即可；
（3）当时，，分别求出当时，图象中y的值，当时，和解析式中的x的值，即可求解；
（4）结合图象，分情况讨论即可．
【小问1详解】
，
点图象上，
把点代入，
得；
【小问2详解】

，
∴图象的顶点坐标为，
当时，函数，
∴图象与x轴的交点为
由图象可知，直线l与x轴平行，且与图象G有三个交点时，，
设直线l解析式为，
联立，整理得，
设，
，，
，
，
即直线l解析式为，
当时，解得（负舍），
所以，点C的坐标为；
【小问3详解】
当时，，
当时，；
当时，
代入解析式为，解得；
代入解析式为，解得（负舍）；
；
【小问4详解】
由点P坐标为，可知点P在直线上，
当时，矩形与图象G恒有两个公共点（如图③）；

当时，矩形与图象G有0个公共点（如图④）；
当时，
，解得；
矩形与图象G有2个公共点（如图⑤）；

当时，矩形与图象G有3个或4个个公共点（如图⑥，⑦，⑧）；

综上，或．
【点睛】本题考查了二次函数的图象和性质，矩形的性质，二次函数与几何综合，一元二次方程根与系数的关系等，熟练掌握并综合运用知识点是解题的关键．