2022-2023学年度吉林省长市吉大附中力旺校区九年级上学期第一次月考数学试题

吉大力旺2022-2023学年度上学期九年级第一次月考数学试卷

一、选择题（本大题共8小题，每小题3分，共24分）

1. 相反数是（    ）

A. 3 B.  C. 9 D.

2. 2020年是全面打赢脱贫攻坚战收官之年，现有贫困人口5520000人今年脱贫，将数据5520000用科学记数法表示为（    ）

A.  B.  C.  D.

3. 如图，一个由圆柱和长方体组成几何体水平放置，它的俯视图是（　　）

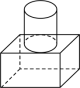
A. 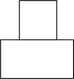   B.    C.    D.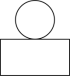  

4. 下列用数轴表示不等式的解集正确的是（    ）

A.  B.  C.  D.

5. 若，则值为（    ）

A. 1 B.  C. 2 D.

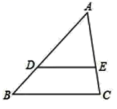
6. 如图，已知分别为上的两点，且，则的长为（    ）

A. 3 B. 6 C. 9 D. 12

7. 如图，依据尺规作图的痕迹，计算（    ）

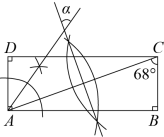
A.  B.  C.  D.

8. 如图，在平面直角坐标系中存在菱形，点的坐标为，点的坐标为，轴，当函数的图象与菱形有两个公共点，的取值范围是（    ）

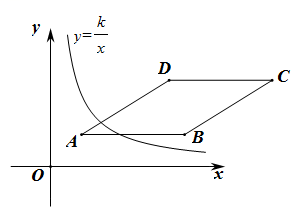
A.  B.  C.  D.

二、填空题（本大题共6小题，每小题3分，共18分）

9. 因式分解：__________．

10. 正方形的对角线长为，则它的面积为________（用含的代数式表示）．

11. 一元二次方程根的判别式的值为_______．

12. 如图，直线过正方形的顶点，点到的距离分别是2和3，则正方形的边长是________．

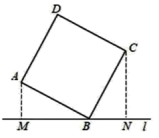
13. 如图，将边长为的正方形沿其对角线剪开，再把沿着方向平移，得到，当两个三角形重叠部分的面积占面积的一半时，平移的距离是________．

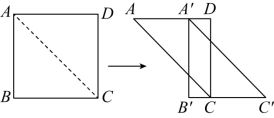
14. 已知一次函数，当变化时，原点到一次函数的图象的最大距离为________．

三、解答题（本大题共10小题，共78分）

15. 先化简，再求值：，其中．

16. 有三张正面分别画有等边三角形、矩形、菱形的不透明卡片，它们除正面图案外都相同．现将它们洗匀后背面朝上（图案为等边三角形的卡片记为，图案为矩形的卡片记为，图案为菱形的卡片记为）．

（1）从这三张卡片中随机抽出一-张 正面图案是菱形的概率为_______ ；

（2）从三张卡片中随机地抽出一张， 记住图案后将卡片放回，洗匀后，再从这三张卡片中随机抽出一张，记住图案．用列表或树状图的方法，求两次抽取的卡片上的图案皆为中心对称图形的概率．

17. 如图，在的正方形网格中，每个小正方形的边长均为1，线段的端点在格点上，按下列三个要求在每个网格中分别作出一个四边形（共需作出两个四边形）；

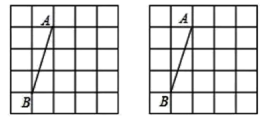
（1）以为边的格点四边形（顶点都在格点上）；

（2）轴对称图形；

（3）互相之间不全等．

18. 今年新冠肺炎疫情在全球肆虐，为降低病亡率，某工厂平均每天比原计划多生产10台呼吸机，现在生产120台呼吸机的时间与原计划生产90台呼吸机所需时间相同．求该工厂原来平均每天生产多少台呼吸机？

19. 某市教育行政部门为了解初三学生每学期参加综合实践活动的情况，随机抽样调查了某校初三学生一个学期参加综合实践活动的天数，并用得到的数据绘制了下面两幅不完整的统计图（如图）．请你根据图中提供的信息，回答下列问题：

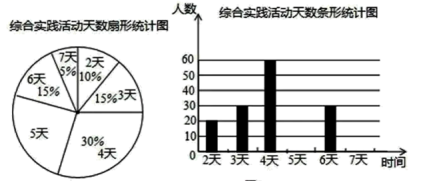
（1）该校初三学生总数为________人；

（2）补全频数分布直方图；

（3）扇形统计图中“活动时间为5天”的扇形所对圆心角的度数是_________；

（4）在这次抽样调查中，众数和中位数分别是_______、________；

（5）如果该市共有初三学生96000人，请你估计“活动时间不少于5天”的大约有________人．

20. （1）如图①，在正方形中，点为上一点，交于，垂足为．求证：；

（2）如图②，在正方形中，点为上一点，点为上一点，分别交于，垂足为点．若正方形的边长为12，，则四边形的面积为_______．

21. 一个水池有进水管和出水管各一个，进水管每分进水，出水管每分出水．水池在开始5min内只进水不出水，随后15min内既进水又出水．水池内的水量与经过的时间之间的函数关系如图．

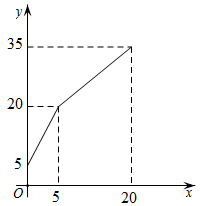
（1）求的值；

（2）若水池从第20min开始只出水不进水，

①求这段时间内与之间的函数关系式；（要求写出自变量的取值范围）

②在水池整个进出水过程中，当水池中的水量为时，直接写出的值．

22. 【教材呈现】如图是华师版九年级上册数学教材第103页的部分内容．

已知：如图，在中，，是斜边上的中线．

求证：．

证明：延长至点，使，连结．

问题解决】补全以上证明过程．

证明：延长至点，使，连接．

【规律探索】如图，在中，于点于点；点是中点，连结，若，则_______．

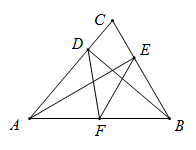
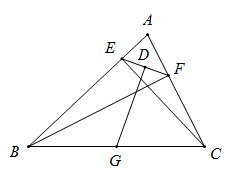
【结论应用】如图，分别是的高线，连结．分别是的中点，则的长为_______．

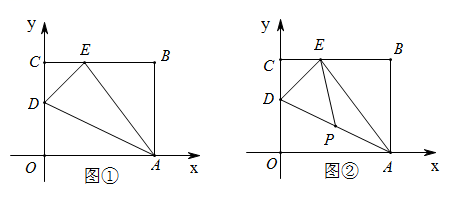
23. 如图①，四边形是一张放在平面中的矩形纸片，．在 边上取一点，将纸片沿翻折，使点落在边上的点处．

（1）_______，_________；

（2）求的长；

（3）如图②，若上有一动点（不与重合）自点沿向终点匀速运动，运动的速度为每秒个单位长度，设运动的时间为秒，连结，设，

①直接写出与时间之间的函数关系式；

②当以点为顶点的三角形为等腰三角形时，求时间的值．

24. 函数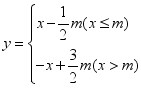的图象记为（为常数），当与轴存在两个交点时，设交点为和（点在点的左侧），

（1）当时，直接写出与时间之间函数的关系式；

（2）当时，求出点和点的坐标；

（3）当在部分的最高点到轴的距离为2时，求的值；

（4）点的坐标为，点的坐标为，当与线段有且仅有一个公共点时，直接写出的取值范围．