（沪教版）2022-2023学年度第一学期九年级数学26.3 二次函数y=ax2+bx+c的图像 同步测试

这是一份（沪教版）2022-2023学年度第一学期九年级数学26.3 二次函数y=ax2+bx+c的图像 同步测试，文件包含沪教版2022-2023学年度第一学期九年级数学263二次函数yax2+bx+c的图像同步测试学生版docx、沪教版2022-2023学年度第一学期九年级数学263二次函数yax2+bx+c的图像同步测试教师版docx等2份试卷配套教学资源，其中试卷共30页， 欢迎下载使用。


（沪教版）2022-2023学年度第一学期九年级数学26.3 二次函数y=ax2+bx+c的图像 同步测试
一、单选题
1．（2021九上·和平期末）已知二次函数y＝ax2+bx+c（a≠0，a，b，c为常数），如果a＞b＞c，且a+b+c＝0，则它的图象可能是（　　）
A． B．
C． D．
【答案】C
【知识点】二次函数y=ax^2+bx+c的图象
【解析】【解答】解：∵a+b+c=0，
∴函数图象过(1，0)，
排除D；
∵a+b+c=0，a>b>c，
∴a>0，排除A；
由选项B可知，c>0，对称轴x=−b2a=1，得b=−2a<0，与b>c矛盾，排除B，
故答案为：C．
【分析】 二次函数y＝ax2+bx+c 中，由于a+b+c=0，a>b>c，可知函数图象过(1，0)，a＞0，据此排除A、D；由选项B可知c>0，利用对称轴x=−b2a=1可求出b＜0，与b>c矛盾，故排除B，从而得解.
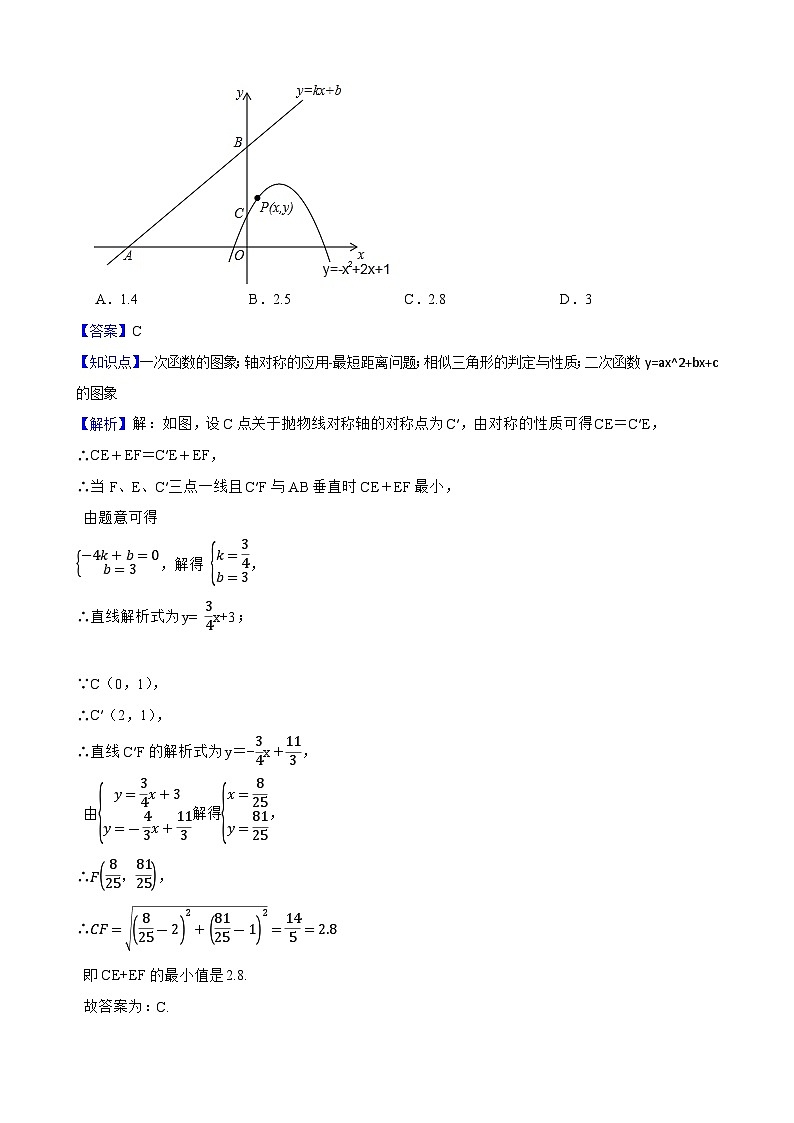
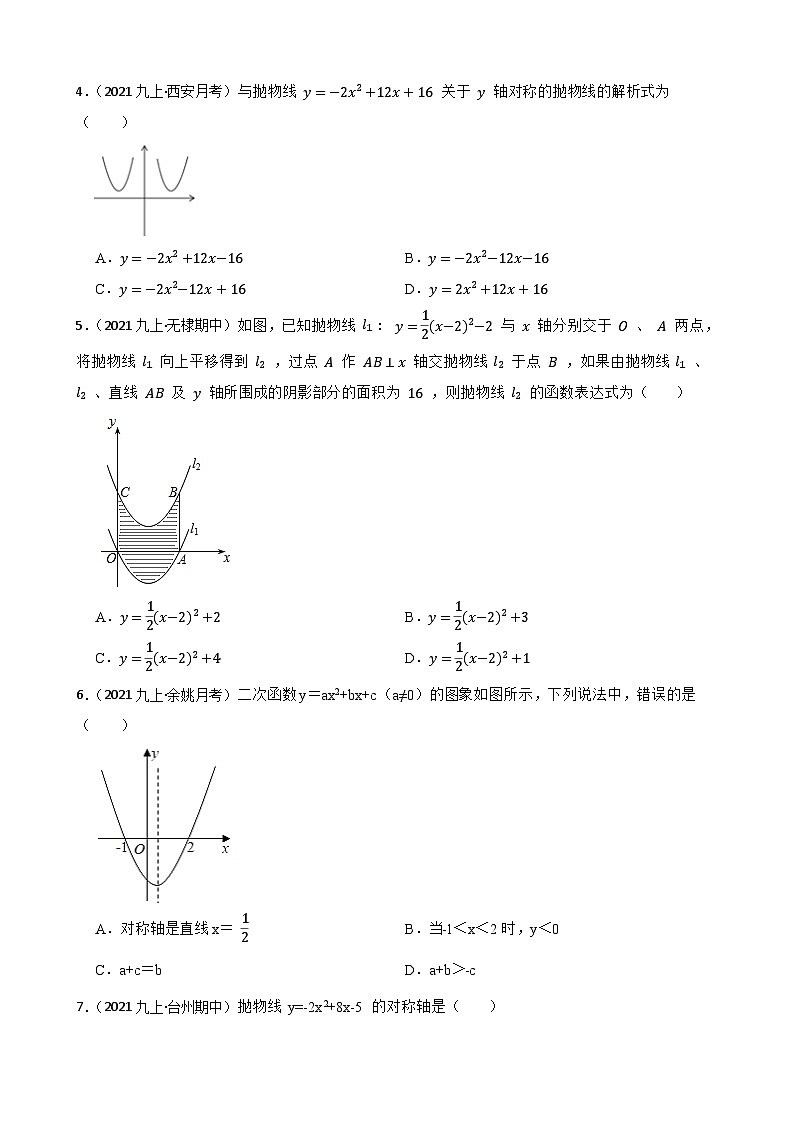
2．（2021九上·宜兴月考）如图，直线y=kx+b（k、b为常数）分别与x轴、y轴交于点A（﹣4，0）、B（0，3），抛物线y=﹣x2+2x+1与y轴交于点C，点E在抛物线y=﹣x2+2x+1的对称轴上移动，点F在直线AB上移动，CE+EF的最小值是（　　）

A．1.4 B．2.5 C．2.8 D．3
【答案】C
【知识点】一次函数的图象；轴对称的应用-最短距离问题；相似三角形的判定与性质；二次函数y=ax^2+bx+c的图象
【解析】解：如图，设C点关于抛物线对称轴的对称点为C′，由对称的性质可得CE＝C′E，
∴CE＋EF＝C′E＋EF，
∴当F、E、C′三点一线且C′F与AB垂直时CE＋EF最小，
由题意可得
−4k+b=0b=3，解得 k=34b=3，
∴直线解析式为y= 34x+3；

∵C（0，1），
∴C′（2，1），
∴直线C′F的解析式为y＝−34x＋113，
由y=34x+3y=-43x+113解得x=825y=8125，
∴F825，8125，
∴CF=825-22+8125-12=145=2.8
即CE+EF的最小值是2.8.
故答案为：C.
【分析】设C点关于抛物线对称轴的对称点为C′，由对称的性质可得CE＝C′E，则可知当F、E、C′三点一线且C′F与AB垂直时CE＋EF最小，由C点坐标可确定出C′，利用互相垂直的直线的斜率乘积等于-1及思安C'的坐标求出直线C'F的解析式，联立两直线解析式组成方程组，求解得出F点的坐标，进而根据平面内两点间的距离公式即可求得CE＋EF的最小值．

3．（2021九上·余杭月考）某二次函数的图象与函数y＝ 12 x2﹣4x＋3的图象形状相同、开口方向一致，且顶点坐标为（﹣2，1），则该二次函数表达式为（　　）
A．y＝ 12 （x﹣2）2＋1 B．y＝ 12 （x﹣2）2﹣1
C．y＝ 12 （x＋2）2＋1 D．y＝﹣ 12 （x＋2）2＋1
【答案】C
【知识点】待定系数法求一次函数解析式；二次函数y=ax^2+bx+c的图象
【解析】【解答】解：设二次函数的解析式为 y=a(x−h)2+k(a≠0) ，
∵二次函数的图象顶点坐标为（﹣2，1），
∴二次函数的解析式为 y=a(x+2)2+1 ，
∵二次函数的图象与函数y＝ 12 x2﹣4x＋3的图象形状相同、开口方向一致，
∴二次函数的解析式为： y=12(x+2)2+1 ，
故答案为：C.
【分析】根据顶点坐标可设二次函数的解析式为y=a(x+2)2+1，由两二次函数的形状、开口方向相同可得a相同，据此可得二次函数的表达式.
4．（2021九上·西安月考）与抛物线 y=−2x2+12x+16 关于 y 轴对称的抛物线的解析式为（　　）

A．y=−2x2+12x−16 B．y=−2x2−12x−16
C．y=−2x2−12x+16 D．y=2x2+12x+16
【答案】C
【知识点】关于坐标轴对称的点的坐标特征；二次函数y=ax^2+bx+c的图象
【解析】【解答】解 ：∵y=-2x2+12x+16=-2（x-3）2+34，顶点坐标为（3，34），
且（3，34）关于y轴对称的点的坐标为（-3，34），
而两抛物线关于y轴对称时形状不变，
∴y=-2x2+12x+16关于y轴对称的抛物线的解析式为y=-2（x+3）2+34=-2x2-12x+16.
故答案为：C.
【分析】将抛物线解析式化为顶点式可得顶点坐标为（3，34），其关于y轴的对称点的坐标为（-3，34），易知两抛物线形状相同，据此可得抛物线的解析式.
5．（2021九上·无棣期中）如图，已知抛物线 l1： y=12(x−2)2−2 与 x 轴分别交于 O 、 A 两点，将抛物线 l1 向上平移得到 l2 ，过点 A 作 AB⊥x 轴交抛物线 l2 于点 B ，如果由抛物线 l1 、 l2 、直线 AB 及 y 轴所围成的阴影部分的面积为 16 ，则抛物线 l2 的函数表达式为（　　）

A．y=12(x−2)2+2 B．y=12(x−2)2+3
C．y=12(x−2)2+4 D．y=12(x−2)2+1
【答案】A
【知识点】平移的性质；二次函数y=ax^2+bx+c的图象
【解析】【解答】当y＝0时，有 12 （x−2）2−2＝0，
解得：x1＝0，x2＝4，
∴OA＝4．
∵S阴影＝OA×AB＝16，
∴AB＝4，
∴抛物线 l2 的函数表达式为y＝ 12 （x−2）2−2＋4＝ y=12(x−2)2+2
故答案为：A．


【分析】根据题意可知阴影部分的面积就是矩形ABCO的面积，由抛物线的解析式可得点O，A的坐标，从而可求OA得长度，再由矩形的面积求得AB的长，即可得到答案。
6．（2021九上·余姚月考）二次函数y＝ax2+bx+c（a≠0）的图象如图所示，下列说法中，错误的是（　　）

A．对称轴是直线x＝ 12 B．当﹣1＜x＜2时，y＜0
C．a+c＝b D．a+b＞﹣c
【答案】D
【知识点】二次函数y=ax^2+bx+c的图象
【解析】【解答】解：A、对称轴是直线x＝ −1+22 ＝ 12 ，故选项A不符合题意；
B、由函数图象知，当﹣1＜x＜2时，函数图象在x轴的下方，
∴当﹣1＜x＜2时，y＜0，故选项B不符合题意；
C、由图可知：当x＝﹣1时，y＝a﹣b+c＝0，
∴a+c＝b，故选项C不符合题意；
D、由图可知：当x＝1时，y＝a+b+c＜0，
∴a+b＜﹣c，故选项D符合题意.
故答案为：D.
【分析】对称轴是直线x＝-1+22＝12，据此判断A；找出在x轴下方图象所对应的x的范围，据此判断B；根据x=-1对应的函数值为0可判断C；根据x=1对应的函数值小于0可判断D.
7．（2021九上·台州期中）抛物线 y=-2x2+8x-5 的对称轴是（　　）
A．x=2 B．x=-2 C．x=4 D．x=-4
【答案】A
【知识点】二次函数y=ax^2+bx+c的图象
【解析】【解答】解：∵y=-2x2+8x+5，
∴对称轴x=-b2a=8-2×-2=2.
故答案为：B.

【分析】根据抛物线对称轴方程公式求解即可.
8．（2021九上·镇原期中）二次函数y＝﹣2x2+4x+3的图象的顶点坐标是（　　）
A．（1，5） B．（﹣1，5） C．（1，3） D．（﹣1，3）
【答案】A
【知识点】二次函数y=ax^2+bx+c的图象
【解析】【解答】解：y＝﹣2x2+4x+3＝﹣2（x﹣1）2+5，
∴该函数的顶点坐标是（1，5）.
故答案为：A.
【分析】首先利用配方法将二次函数的解析式化为顶点式“y=（x-h)2+k”，根据顶点式得出其顶点坐标为（h，k），据此可得答案.
9．（2021九上·沂源期中）已知二次函数y＝2 x2 ﹣8x+6的图象交x轴于A，B两点．若其图象上有且只有 P1 ， P2 ， P3 三点满足 S△ABP1=S△ABP2=S△ABP3 =m，则m的值是（　　）
A．1 B．32 C．2 D．4
【答案】C
【知识点】三角形的面积；二次函数y=ax^2+bx+c的图象
【解析】【解答】∵数y＝2 x2 ﹣8x+6
= 2(x−2)2−2 ，
∴抛物线的顶点坐标为（2，-2），
∵2(x−2)2−2=0 ，
解得 x1=1 ， x2=3 ，

∴AB=3-1=2，
∵S△ABP1=S△ABP2=S△ABP3 =m，
∴P1 ， P2 ， P3 到AB的距离相等，
如图所示，三角形的高为2，
∴m= 12×2×2 =2，
故答案为：C．

【分析】先画出函数的草图，再根据S△ABP1=S△ABP2=S△ABP3可得P1 ， P2 ， P3 到AB的距离相等，结合图象可得三角形的高为2，再利用三角形的面积公式计算即可。
10．（2021九上·新丰期中）二次函数y = x2-2x-3的图象如图所示，则函数值y<0时，x的取值范围是（　　）

A．-1 C．x>3 D．x<-1或 x>3
【答案】A
【知识点】二次函数y=ax^2+bx+c的图象
【解析】【解答】解：∵二次函数y= x2－2x－3的图象如图所示．

∴图象与x轴交在（-1，0），（3，0），
∴当y＜0时，即图象在x轴下方的部分，此时x的取值范围是：-1＜x＜3．
故答案为：A．
【分析】利用函数解析式求出抛物线与x轴的交点坐标，再利用图象直接得出x轴下方图象所对应的x的范围即可.
二、填空题
11．（2021九上·澄海期末）二次函数y=ax2+bx+c图象上部分点的坐标满足下表：
x
…
-3
-2
-1
0
1
…
y
…
-3
-2
-3
-6
-11
…
则该函数图象的顶点坐标为　 　
【答案】（-2，-2）
【知识点】二次函数y=ax^2+bx+c的图象
【解析】【解答】∵x=−3和−1时的函数值都是−3相等，
∴二次函数的对称轴为直线x=−2，
∴顶点坐标为(−2，−2).

【分析】根据表格可得：x=−3和−1时的函数值都是−3相等，即可得到二次函数的对称轴为直线x=−2，再结合表格可得：顶点坐标为(−2，−2)。
12．（2021九上·东莞期末）若点（m，0）在二次函数y＝x2﹣3x+2的图象上，则2m2﹣6m+2029的值为 　 　．
【答案】2025
【知识点】代数式求值；二次函数y=ax^2+bx+c的图象
【解析】【解答】解：∵ 点（m，0）在二次函数y＝x2﹣3x+2的图象上，
∴m2−3m+2=0
即m2−3m=−2；
∴2m2﹣6m+2029=2(m2−3m)+2029=2×(−2)+2029=2025；
故应填2025．

【分析】将点（m，0）代入二次函数函数可得m2−3m+2=0，再将代数式 2m2﹣6m+2029变形为2(m2−3m)+2029，再计算即可。
13．（2021九上·虹口期末）已知二次函数y=(a−1)x2+x+a2−1的图像经过原点，则a的值是　 　．
【答案】−1
【知识点】二次函数y=ax^2+bx+c的图象
【解析】【解答】解：∵二次函数y=(a−1)x2+x+a2−1的图像经过原点(0，0)
∴a−1≠0a2−1=0
∴a=−1．
故答案是：−1

【分析】将点（0，0）代入二次函数解析式y=(a−1)x2+x+a2−1求出a的值即可。
14．（2022八下·北仑期末）二次函数y=x2−4x+5的对称轴为x=　 　．
【答案】2
【知识点】二次函数y=ax^2+bx+c的图象
【解析】【解答】解： y=x2−4x+5
=(x-2)2+1，
∴对称轴x=2.
故答案为：2.

【分析】先把函数化成顶点式y=a(x-h)2+k，根据对称轴x=h解答即可.
15．（2022·旌阳模拟）抛物线 y=ax2+bx+c （ a≠0 ）的对称轴为 x=−1 ，经过点（1，n），顶点为P，下列四个结论：
①若 a<0 ，则 c>n ；
②若c与n异号，则抛物线与x轴有两个不同的交点；
③方程 ax2+(b−n)x+c=0 一定有两个不相等的实数解；
④设抛物线交y轴于点C，不论a为何值，直线PC始终过定点（3，n）.
其中正确的是　 　（填写序号）.
【答案】①②④
【知识点】二次函数图象与坐标轴的交点问题；二次函数y=ax^2+bx+c的图象
【解析】【解答】解：∵抛物线 y=ax2+bx+c （ a≠0 ）的对称轴为 x=−1 ，
∴x=−b2a=−1 ，即b=2a，
∵抛物线过点（1，n），
∴a+b+c=n，即3a+c=n，
∴n-c=3a， a=n−c3 ，
若a<0，则n-c<0，即n ∆= b2−4ac = 4a2−4ac
=4a（a-c）
= 43(n−c)(n−c3−c)
= 49(n2−5nc+4c2) ，
∵c、n异号，
∴∆>0，则抛物线与x轴有2个交点，故②正确；
方程 ax2+(b−n)x+c=0 ，
∆= (b−n)2−4ac=(a−c)2 ，
当a=c时，∆=0，方程只有一个实数根；
当a ≠ c时∆>0，方程有2个实数根，故③错误；
∵P为抛物线 y=ax2+bx+c 顶点，
∴P坐标为（-1，-a+c），
∵点C坐标为（0，c），
直线PC的解析式为y=ax+c，
又 a=n−c3 ，则y= (n−c)3 x+c，
点（3，n），
当x=3时y=n-c+c=n，
∴直线PC始终过（3，n），故④正确.
故答案为：①②④.
【分析】根据抛物线的对称轴为直线x=-1可得b=2a，将（1，n）代入可得3a+c=n，表示出a，据此判断①；根据∆=b2-4ac可得∆，然后结合c、n异号确定出∆的正负，据此判断②；同理表示出∆，根据其结果的正负可判断③；易得P（-1，-a+c），表示出直线PC的解析式，令x=3，可得y=n，据此判断④.
三、解答题
16．（2021九上·镇平县期末）二次函数y＝ax2＋bx＋c的图象经过点A（4，0），B（0，﹣3），C（﹣2，0），求它的解析式，直接写出它的开口方向、对称轴和顶点坐标.
【答案】解：∵A（4，0），B（0，－3），C（－2，0），
∴c=−316a+4b+c=04a−2b+c=0
解得：a=38，b=−34，C＝－3，
∴二次函数解析式为：y=38x2−34x−3.
∵a=38>0，
∴二次函数的图象开口向上；
∵−b2a=−−342×38=1，
∴二次函数的对称轴为x＝1；
将x=1代入y=38x2−34x−3得：y=−278，
∴二次函数的顶点坐标为（1，−278）.
【知识点】待定系数法求二次函数解析式；二次函数y=ax^2+bx+c的图象
【解析】【分析】由题意把点A、B、C的坐标代入二次函数 y＝ax2＋bx＋c ，可得关于a、b、c的方程组，解方程组可求得二次函数的解析式，由a的符号可判断二次函数的图象开口向上；根据对称轴x=-b2a可求得二次函数的对称轴为x＝1；把对称轴x=1的值代入二次函数的解析式求得y的值，即为顶点坐标.
17．（2022九上·金东期末）已知抛物线y=x2+bx−3（b是常数）经过点A(−1，0).求该抛物线的解析式和顶点坐标.
【答案】解：∵抛物线y=x2+bx−3（b是常数）经过点A(−1，0)，
∴把点A坐标代入解析式得(−1)2+b×(−1)−3=0，
解得：b=-2，
∴抛物线解析式为：y=x2−2x−3，
把抛物线配方得y=(x2−2x+1)−3−1=(x−1)2−4，
抛物线的顶点坐标为（1，-4）.
【知识点】二次函数图象上点的坐标特征；二次函数y=ax^2+bx+c的图象
【解析】【分析】 把点A坐标代入抛物线y=x2+bx-3求出b值即得解析式，再将解析式化为顶点式即得顶点坐标.
18．（2021九上·萧山月考）已知点（0，3）在二次函数 y=ax2+bx+c 的图象上，且当 x=1 时，函数 y 有最小值2，这个二次函数的表达式。
【答案】解：∴点（1，2）为抛物线的顶点，
于是可设抛物线的关系式为y＝a（x﹣1）2+2，把（0，3）代入得，
a+2＝3，
∴a＝1，
∴抛物线的关系式为y＝（x﹣1）2+2，
即y＝x2﹣2x+3；
【知识点】二次函数的最值；二次函数y=ax^2+bx+c的图象
【解析】【分析】根据题意得出抛物线的顶点坐标，然后根据顶点式设函数解析式，代入已知点坐标求出a值，即可解答.
19．（2021七下·沐川期末）在等式y=ax2+bx+c中，当x=0时，y=6；当x=1时，y=5；x=2时，y=5.求a、b、c的值.
【答案】解：把x=0，y=6；x=1，y=5；x=2，y=5分别代入y=ax2+bx+c得c=6a+b+c=54a+2b+c=5，解得a=12b=−32c=6
∴a=12，b=−32，c=6.
【知识点】三元一次方程组解法及应用；二次函数y=ax^2+bx+c的图象
【解析】【分析】分别将x=0、y=6；x=1、y=5；x=2、y=5代入y=ax2+bx+c中就可求出a、b、c的值.
20．（2020九上·莲湖月考）求下列二次函数图象的对称轴和顶点坐标： y=2x2+12x+21 .
【答案】解： y=2x2+12x+21
=2(x2+6x+9−9)+21
=2(x+3)2−18+21
=2(x+3)2+3
∴对称轴为直线 x=−3 ，顶点坐标为( −3 ，3).
【知识点】二次函数y=ax^2+bx+c的图象
【解析】【分析】利用配方法将函数解析式转化为顶点式，利用二次函数y=a（x-h）2+k的顶点坐标为（h，k），对称轴直线为x=h即可直接得出答案.
21．（2020九上·亳州月考）若二次函数y=ax2+bx+c的图象的顶点是（2，1）且经过点（1，2），求此二次函数解析式．
【答案】解： 根据二次函数的顶点坐标，
设二次函数的解析式为y=a（x-2）2+1
将点（1,2）的坐标代入
a=1
∴y=x2-4x+4+1=x2-4x+5
【知识点】二次函数y=ax^2+bx+c的图象；二次函数y=ax^2+bx+c的性质
【解析】【分析】根据题意，设出二次函数的顶点式，将点（1,2）代入方程，求出解析式即可。
22．（2020九上·亳州月考）已知点 P(m,n) 在以y轴为对称轴的抛物线 y=x2+ax+4 上，求 2m−n 的最大值．
【答案】解：∵二次函数 y=x2+ax+4 的对称轴是直线x=0
∴−a2×1=0
∴a=0
∴该二次函数的解析式为： y=x2+4
∵点 P(m,n) 在该函数 y=x2+4 的图象上
∴n=m2+4
∴2m−n
=−m2+2m−4
=−(m−1)2−3
∴当m=1时， 2m−n 取得最大值-3．
【知识点】二次函数的最值；二次函数y=ax^2+bx+c的图象
【解析】【分析】根据该二次函数的对称轴为y轴可得a=0，进而得到函数解析式为 y=x2+4 ，再根据点 P(m,n) 在该函数 y=x2+4 的图象上，可得 2m−n=−(m−1)2−3 ，即可求解．
23．（2020九上·湖北月考）如图，抛物线y=x2+bx+c与y轴交于点A（0，2），对称轴为直线x=2，求此抛物线的解析式.

【答案】解：由题意得：x=- b2a =- b2 =-2，c=2，
解得：b=4，c=2，
则此抛物线的解析式为y=x2+4x+2.
【知识点】待定系数法求二次函数解析式；二次函数y=ax^2+bx+c的图象
【解析】【分析】由对称轴直线x=2，确定出b的值，将A点坐标代入函数解析式即可确定c的值，即可求出抛物线解析式.
24．（2020九上·亳州月考）如图，是某座抛物线型的隧道示意图，已知路面AB宽24米，抛物线最高点C到路面AB的距离为8米，为保护来往车辆的安全，在该抛物线上距路面AB高为6米的点E，F处要安装两盏警示灯，求这两盏灯的水平距离EF.（提示：以AB所在的直线为x轴，抛物线的对称轴为y轴建立平面直角坐标系）

【答案】解：设 y=ax2+8
求出 a=−118
写出解析式 y=−118x2+8
把 y=6 代入求出 x=±6 ，写出点 E 、 F 的坐标
EF=12
【知识点】二次函数y=ax^2+bx+c的图象；二次函数y=ax^2+bx+c的性质
【解析】【分析】根据待定系数法求出抛物线的解析式，根据题意即可得到点E和点F两点的纵坐标，代入抛物线即可得到横坐标，求出EF的距离即可。