【同步学案】苏教版（2019） 高中数学 必修第二册 第9章平面向量学案含解析

9.2.2　向量的数乘

知识点1　向量的数乘定义

一般地，实数λ与向量a的积是一个向量，记作λa，它的长度和方向规定如下：

(1)|λa|＝|λ||a|；

(2)若a≠0，则当λ＞0时，λa与a方向相同；当λ＜0时，λa与a方向相反．

实数λ与向量a相乘的运算，叫作向量的数乘．

特别地，当λ＝0时，0a＝0；当a＝0时，λ0＝0．

向量的数乘λa的几何意义：当λ＞0时，把向量a沿着a的相同方向放大或缩小；当λ＜0时，把向量a沿着a的相反方向放大或缩小．

1．λa＝0，一定能得到λ＝0吗？

[提示]　不一定．λa＝0，则λ＝0或a＝0．

1．思考辨析(正确的画“√”，错误的画“×”)

(1)a＝0，则λa＝0． (　　)

(2)对于非零向量a，向量－3a与向量3a方向相反． (　　)

(3)对于非零向量a，向量－6a的模是向量3a的模的2倍． (　　)

[答案]　(1)√　(2)√　(3)√

知识点2　向量数乘的运算律

设a，b为向量，λ，μ为实数，则

(1)λ(μa)＝(λμ)a；

(2)(λ＋μ)a＝λa＋μa；

(3)λ(a＋b)＝λa＋λb．

向量的加法、减法和数乘统称为向量的线性运算．

2．(1)5×(－4a)＝________．

(2)a＝e1＋2e2，b＝3e1－2e2，则a＋b＝________．

(1)－20a　(2)4e1　[(1)5×(－4a)＝5×(－4)a＝－20a．

(2)a＋b＝(e1＋2e2)＋(3e1－2e2)＝4e1．]

知识点3　向量共线定理

一般地，对于两个向量a(a≠0)，b，设a为非零向量，如果有一个实数λ，使b＝λa，那么b与a是共线向量；反之，如果b与a是共线向量，那么有且只有一个实数λ，使b＝λa．

2．向量共线定理中，为什么规定a≠0．

[提示]　当a＝0时，显然b与a共线，此时若b＝0，则存在无数实数λ，使b＝λa；若b≠0，则不存在实数λ使得b＝λa．

3．已知e1和e2不共线，则下列向量a，b共线的序号是____．

①a＝2e1，b＝2e2；

②a＝e1－e2，b＝－2e1＋2e2；

③a＝4e1－e2，b＝e1－e2；

④a＝e1＋e2，b＝2e1－2e2．

②③　[∵e1与e2不共线，∴①不正确；

对于②有b＝－2a；对于③有a＝4b；④不正确．]

类型1　向量数乘的基本运算

【例1】　计算：

(1)6(3a－2b)＋9(－2a＋b)；

(2)－；

(3)6(a－b＋c)－4(a－2b＋c)－2(－2a＋c)．

[解]　(1)原式＝18a－12b－18a＋9b＝－3b．

(2)原式＝－

＝a＋b－a－b－a－b－a＝0．

(3)原式＝6a－6b＋6c－4a＋8b－4c＋4a－2c＝6a＋2b．

向量的数乘运算类似于代数多项式的运算，主要是“合并同类项”“提取公因式”，但这里的“同类项”“公因式”指向量，实数看作是向量的系数.向量也可以通过列方程来解，把所求向量当作未知量，利用解代数方程的方法求解.

[跟进训练]

1．若向量a＝3i－4j，b＝5i＋4j，则－3＋(2b－a)＝________．

－16i＋ j　[原式＝a－b－3a－2b＋2b－a

＝－a－b

＝－(3i－4j)－(5i＋4j)

＝(－11－5)i＋ j

＝－16i＋j．]

类型2　向量的共线问题

【例2】　已知非零向量e1，e2不共线．

(1)如果＝e1＋e2，＝2e1＋8e2，＝3(e1－e2)，求证：A，B，D三点共线．

(2)欲使ke1＋e2和e1＋ke2共线，试确定实数k的值．

1欲证A，B，D三点共线，能否证明与或共线？

2若ke1＋e2与e1＋ke2共线，则两向量间存在怎样的等量关系？

[解]　(1)证明：∵＝e1＋e2，＝＋＝2e1＋8e2＋3e1－3e2＝5(e1＋e2)＝5，

∴，共线，且有公共点B，∴A，B，D三点共线．

(2)∵ke1＋e2与e1＋ke2共线，∴存在实数λ，使ke1＋e2＝λ(e1＋ke2)，则(k－λ)e1＝(λk－1)e2，由于e1与e2不共线，只能有∴k＝±1．

1．证明三点共线，通常转化为证明这三点构成的其中两个向量共线，向量共线定理是解决向量共线问题的依据．

2．若A，B，C三点共线，则向量，，在同一直线上，因此必定存在实数，使得其中两个向量之间存在线性关系．而向量共线定理是实现线性关系的依据．

[跟进训练]

2．(对接教材P19T11)已知O，A，M，B为平面上四点，且＝λ＋(1－λ)(λ∈R，λ≠0且λ≠1)．

(1)求证：A，B，M三点共线；

(2)若点B在线段AM上，求实数λ的取值范围．

[解]　(1)证明：∵＝λ＋(1－λ)，

∴＝λ＋－λ，

－＝λ－λ，

∴＝λ(λ∈R，λ≠0，且λ≠1)．

又与有公共点A，∴A，B，M三点共线．

(2)由(1)知＝λ，

若点B在线段AM上，则与同向，

∴||>||>0，∴λ>1．

类型3　向量的表示

【例3】　如图所示，已知△OAB中，点C是以A为对称中心的B点的对称点，D是把分成2∶1的一个内分点，DC和OA交于E，设＝a，＝b．

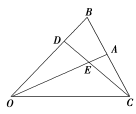
(1)用a和b表示向量，；

(2)若＝λ，求实数λ的值．

[解]　(1)依题意，A是BC中点，

∴2＝＋，

即＝2－＝2a－b，

＝－＝－

＝2a－b－b＝2a－b．

(2)若＝λ，

则＝－＝λa－(2a－b)＝(λ－2)a＋b．

∵与共线，

∴存在实数k，使＝k，

∴(λ－2)a＋b＝k，解得λ＝．

用已知向量表示未知向量的求解思路

(1)先结合图形的特征，把待求向量放在三角形或平行四边形中；

(2)然后结合向量的三角形法则或平行四边形法则及向量共线定理，用已知向量表示未知向量；

(3)求解过程体现了数学上的化归思想．

[跟进训练]

3．(1)设O是△ABC内部一点，且＋＝－3，则△AOB与△AOC的面积之比为________．

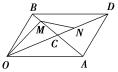
(2)如图，在▱OADB中，设＝a，＝b，＝，＝．试用a，b表示＝________．

(1)　(2)a－b　[(1)如图，由平行四边形法则，知＋＝，其中E为AC的中点．

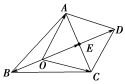
所以＋＝2＝－3．

所以＝－，||＝||．

设点A到BD的距离为h，则S△AOB＝||·h，S△AOC＝2S△AOE＝||·h．

所以＝＝＝×＝．

(2)由题意知，在▱OADB中，＝＝＝(－)＝(a－b)＝a－b．

则＝＋＝b＋a－b＝a＋b，

＝＝(＋)＝(a＋b)＝a＋b，

＝－＝a＋b－a－b＝a－b．]

1．已知线段上A，B，C三点满足＝2，则这三点在线段上的位置关系是(　　)

A　　　　　　　B

C　　　　　　　D

[答案]　A

2．(多选题)若＝4，则下列各式中正确的是(　　)

A．＝3   B．＝3

C．＝   D．＝

BCD　[由＝4可知＝－＝－4＝－3＝3，故A错误，B正确；同理可知＝，＝，故选BCD．]

3．已知m∈R，下列说法正确的是(　　)

A．若ma＝0，则必有a＝0

B．若m≠0，a≠0，则ma与a方向相同

C．m≠0，a≠0，则|ma|＝m|a|

D．若m≠0，a≠0，则ma与a共线

D　[A错．若ma＝0，则m＝0或a＝0；

B错．m＞0时，ma与a同向，m＜0时，ma与a反向；

C错．∵|ma|＝|m||a|，∴m＞0时，|ma|＝m|a|；m＜0时，|ma|＝－m|a|．]

4．△ABC中，E，F分别是AB，AC的中点，且＝a，＝b，则＝________(用a，b表示)．

(b－a)　[＝－＝－＝(b－a)．]

5．若＝5e，＝－7e，且||＝||，则四边形ABCD的形状是________．

等腰梯形　[∵＝5e，＝－7e，

∴＝－，

∴与平行且方向相反，易知||＞||．

又∵||＝||，

∴四边形ABCD是等腰梯形．]

回顾本节知识，自我完成以下问题：

1．如何描述向量λa的大小、方向？

[提示]　向量λa的大小为：|λa|＝|λ||a|；

向量λa的方向与实数λ有关：当λ>0时，λa的方向与a相同；

当λ＝0时，λa的方向具有任意性；

当λ<0时，λa的方向与a相反．

2．若＝x＋y，则A，B，P三点共线的充要条件是什么？

[提示]　x＋y＝1．

3．若向量a，b共线，且a≠0，则a与b存在怎样的等量关系？

[提示]　b＝λa，其中λ是唯一确定的实数．