【同步学案】苏教版（2019） 高中数学 必修第二册 第11章解三角形学案含解析

第2课时　正弦定理(2)

问题：∠A＝60°，b＝4，a为何值时，作出的三角形是唯一的？

知识点1　解三角形的类型

(1)已知三角形的两角和任意一边，求另两边和另一角，此时有唯一解，三角形被唯一确定．

(2)已知两边和其中一边的对角，求其他的边和角，此时可能出现一解、两解或无解的情况．

如已知两边a，b和a的对角A，解的情况如下表：

1．在△ABC中，根据下列条件解三角形，其中无解的是________；有一解的是________；有两解的是________．

①a＝7，b＝3，B＝30°；

②b＝6，c＝5，B＝45°；

③a＝15，b＝10，B＝120°；

④b＝6，c＝6，C＝60°．

①③　④　②　[对于①，由正弦定理，得sin A＝sin B＝sin 30°＝>1，所以此三角形无解；

对于②，由正弦定理，得sin C＝sin B＝sin 45°＝<1，且c>b，所以此三角形有两解；

对于③，由正弦定理，得sin A＝sin B＝sin 120°＝>1，所以此三角形无解；

对于④，由正弦定理，得sin B＝sin C＝sin 60°＝<1，且c>b，所以B<C，B＝30°，A＝90°，所以此三角形只有一解．]

知识点2　三角形的面积公式

任意三角形的面积公式为：

(1)S△ABC＝bcsin A＝acsin B＝absin C，即任意三角形的面积等于任意两边与它们夹角的正弦的乘积的一半．

(2)S△ABC＝ah，其中a为△ABC的一边长，而h为该边上的高的长．

(3)S△ABC＝r(a＋b＋c)＝rl，其中r，l分别为△ABC的内切圆半径及△ABC的周长．

(4)S△ABC＝，其中p为△ABC的半周长，即p＝(a＋b＋c)．该公式称为海伦－秦九韶公式，适用于三角形三边为有理数时，计算三角形的面积比较简便．

2．在△ABC中，A，B，C所对的边分别为a，b，c，其中a＝4，b＝3，C＝60°，则△ABC的面积为(　　)

A．3  B．3  C．6  D．6

B　[由S＝absin C＝×4×3×得S＝3，故选B．]

类型1　三角形解的个数的判断

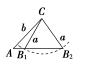
【例1】　已知下列各三角形中的两边及其一边的对角，判断三角形是否有解，有解的作出解答．

(1)a＝10，b＝20，A＝80°；

(2)a＝2，b＝6，A＝30°．

[解]　(1)a＝10，b＝20，a<b，A＝80°<90°，

讨论如下：

∵bsin A＝20sin 80°>20sin 60°＝10，

∴a<bsin A，∴本题无解．

(2)a＝2，b＝6，a<b，A＝30°<90°，

∵bsin A＝6sin 30°＝3，a>bsin A，

∴bsin A<a<b，∴三角形有两解．

由正弦定理得sin B＝＝＝，

又∵B∈(0°，180°)，∴B1＝60°，B2＝120°．

当B1＝60°时，C1＝90°，c1＝＝＝4；

当B2＝120°时，C2＝30°，c2＝＝＝2．

∴B1＝60°时，C1＝90°，c1＝4；B2＝120°时，C2＝30°，c2＝2．

已知两边和其中一边的对角解三角形时，首先求出另一边的对角的正弦值，根据该正弦值求角时，要根据已知两边的大小情况来确定该角有一个值还是两个值，或者根据该正弦值不等于1时在0°～180°范围内求角，一个锐角，一个钝角，只要不与三角形内角和定理矛盾，就是所求.

[跟进训练]

1．△ABC中，a＝x，b＝2，B＝45°．若该三角形有两解，则x的取值范围是________．

(2，2)　[由asin B<b<a，得x<2<x，∴2<x<2．]

类型2　三角形的面积

【例2】　在△ABC中，若a＝2，C＝，cos ＝，求△ABC的面积S．

[解]　∵cos ＝，∴cos B＝2cos2 －1＝．

∴B∈，∴sin B＝．

∵C＝，∴sin A＝sin (B＋C)

＝sin Bcos C＋cos Bsin C＝．

∵＝，

∴c＝＝×＝．

∴S＝acsin B＝×2××＝．

已知三角形的两边和夹角可求三角形的面积，三角形的面积公式为S＝absin C＝acsin B＝bcsin A．

[跟进训练]

2．(1)在△ABC中，若a＝3，cos C＝，S△ABC＝4，则b＝________．

(2)在△ABC中，AB＝，AC＝1，B＝30°，则△ABC的面积等于________．

(1)2　(2)或　[(1)∵cos C＝，

∴C∈(0°，90°)，

∴sin C＝＝，

又S△ABC＝absin C＝×3×b×＝4，

∴b＝2．

(2)由正弦定理得sin C＝＝＝，

又∵C∈(0°，180°)，

∴C＝60°或120°，

∴A＝90°或30°，

∴S△ABC＝AB·AC·sin A＝或．]

类型3　正弦定理的综合应用

【例3】　在△ABC中，角A，B，C所对的边分别是a，b，c，m＝(sin A，sin B)，n＝(cos B，cos A)，m·n＝－sin 2C．

(1)求C的大小；

(2)若c＝2，A＝，求△ABC的面积．

1由m·n＝－sin 2C，利用三角恒等变换求出C的大小；

2由正弦定理可得b的大小，利用三角形的面积公式求解.

[解]　(1)由题意知，m·n＝sin Acos B＋sin Bcos A＝－sin 2C，

即sin(A＋B)＝－sin 2C，sin C＝－2sin Ccos C．

由0<C<π，得sin C>0．

所以cos C＝－，C＝．

(2)由C＝，A＝，得B＝π－A－C＝．

由正弦定理，＝，

即＝，解得b＝2．

所以△ABC的面积S＝bcsin A＝×2×2×sin ＝．

借助正弦定理可以实现三角形中边角关系的互化，转化为角的关系后，常利用三角变换公式进行变形、化简，确定角的大小或关系，继而判断三角形的形状、证明三角恒等式.

[跟进训练]

3．在△ABC中，已知c＝10，＝＝，求a，b及△ABC的内切圆半径．

[解]　由正弦定理知＝，∴＝．

即sin Acos A＝sin Bcos B，

∴sin 2A＝sin 2B．

又∵a≠b且A，B∈(0，π)，

∴2A＝π－2B，即A＋B＝．

∴△ABC是直角三角形且C＝，

由 得a＝6，b＝8．

∴内切圆的半径为r＝＝＝2．

1．在△ABC中，sin A＝sin C，则△ABC是(　　)

A．直角三角形   B．等腰三角形

C．锐角三角形   D．钝角三角形

B　[由正弦定理可得sin A＝sin C⇒＝，即a＝c，所以△ABC为等腰三角形．]

2．在△ABC中，A＝30°，a＝3，b＝2，则这个三角形有(　　)

A．一解   B．两解

C．无解   D．无法确定

A　[由b<a和大边对大角可知三角形的解的个数为一解．]

3．在△ABC中，a，b，c分别是角A，B，C的对边，若a＝1，b＝，B＝60°，则△ABC的面积为(　　)

A．  B．  C．1  D．

B　[∵a＝1，b＝，B＝60°，

∴由正弦定理可得：sin A＝＝＝，

∵a＜b，A＜60°，∴A＝30°，C＝180°－A－B＝90°，

∴S△ABC＝ab＝×1×＝．故选B．]

4．在△ABC中，A＝，a＝c，则＝________．

1　[由＝得sin C＝＝×＝，

又0<C<，

所以C＝，B＝π－(A＋C)＝．

所以＝＝＝1．]

5．在△ABC中，若b＝5，B＝，tan A＝2，则sin A＝________，a＝________．

　2　[由tan A＝2，得sin A＝2cos A，

由sin2A＋cos2A＝1，得sin A＝，

∵b＝5，B＝，

由正弦定理＝，

得a＝＝＝2．]

回顾本节知识，自我完成以下问题：

1．正弦定理的常见变形有哪些？

[提示]　正弦定理的常见变形：

①sin A∶sin B∶sin C＝a∶b∶c；

②＝＝＝＝2R；

③a＝2Rsin A，b＝2Rsin B，c＝2Rsin C；

④sin A＝，sin B＝，sin C＝．

2．正弦定理及其变形体现了怎样的数学思想？

[提示]　正弦定理及其变形体现了转化化归的数学思想．具体如下：

利用正弦定理可以实现三角形中边角关系的相互转化，一方面可以化边为角，转化为三角函数问题来解决；另一方面，也可以化角为边，转化为代数问题来解决．

3．已知三角形的任意两边及一边的对角，如何判断其解的情况？

[提示]　判断方法常有两种：

法一：如下表，过点C作AB的垂线，根据边a与AB边上的高的大小关系来判断解的个数．

法二：由正弦定理＝⇒sin B＝，若sin B>1，则无解；若sin B＝1，则一个解；若0<sin B<1，则由三角形“大边对大角”来确定角B的范围，从而判断解的情况．

秦九韶的“三斜求积术”

你听说过“三斜求积术”吗？这是我国宋代的数学家秦九韶用实例的形式提出的，其实质是根据三角形的三边长a，b，c求三角形面积S，即

S＝．

“三斜求积术”中的“三斜”指三角形的三条边，而且三条边从小到大分别称为“小斜”“中斜”“大斜”．秦九韶是用语言叙述的相关公式，即：以少广求之，以小斜幂并大斜幂，减中斜幂，余半之，自乘于上；以小斜幂乘大斜幂，减上，余四约之，为实；一为从隅，开平方得积．

事实上，利用余弦定理等内容，也可推导出“三斜求积术”，过程如下：

S2＝c2a2sin2B＝(c2a2－c2a2cos2B)，

又因为cacos B＝，

所以

S2＝，

从而可知

S＝．