1.4 有理数的大小比较 基础（解析版） 试卷

这是一份1.4 有理数的大小比较 基础（解析版），共13页。
1.4  有理数的大小比较  基础  一、单选题1．在0,1，-3，-1四个数中，最小的数是（   ）A．0 B．1 C．-3 D．-1【答案】C【解析】【分析】有理数大小比较的法则：①正数都大于0；②负数都小于0；③正数大于一切负数；④两个负数，绝对值大的其值反而小，据此判断即可．【详解】解：∵-3＜-1＜0＜1，
∴-3最小，
故选：C．【点睛】本题考查了有理数比较大小，注意负数的绝对值越大负数越小．2．绝对值小于5.1的整数有（    ）A．5个 B．6个 C．10个 D．11个【答案】D【分析】根据绝对值表示数在数轴上对应的点到原点的距离即可解答．【详解】解：绝对值小于5.1的整数有：±1，±2，±3，±4，±5和0共有11个．
故选：D．【点睛】本题考查了绝对值的定义，绝对值就是数表示的点到原点的距离，理解定义是关键．3．下列各式中正确的是（　　）A．﹣6＜﹣9 B．﹣0.36＜﹣0.66C． D．【答案】C【分析】根据负数比较大小的法则，先比较两个数的绝对值，再确定两个数的大小，即可得出答案.【详解】解：A.因为6<9，所以，所以A错误；B.因为0.36<0.66，所以，所以B错误；C.因为，所以，所以C正确；D. 因为，所以，所以D错误；故答案选C.【点睛】本题考查负数比较大小，先比较两个数的绝对值，再根据负数绝对值大的数反而小，得出比较结果；熟练掌握负数比较大小的方法是解题关键.4．下列四个数的绝对值比2大的是(　　)．A．－3 B．0 C．1 D．2【答案】A【分析】分别求出选项中四个数的绝对值，再与2比较，从而可得答案．【详解】解：因为：所以：>2．故选：A．【点睛】本题考查的是求一个数的绝对值以及有理数的大小比较，掌握以上知识是解题的关键．5．的相反数是(     )A． B． C．-5 D．5【答案】B【解析】【分析】根据只有符号不同的两个数互为相反数解答即可.【详解】的相反数是.故选B.【点睛】本题考查了相反数的定义，解答本题的关键是熟练掌握相反数的定义，正数的相反数是负数，0的相反数是0，负数的相反数是正数.6．下列四个选项表示某水军四个时刻的水位高度（单位：m），其中高度最低的是（    ）A． B．10 C． D．0【答案】A【分析】根据正数与负数在实际生活中的应用、有理数的大小比较法则即可得．【详解】由有理数的大小比较法则得：四个选项的大小关系为则在四个选项中，高度最低的是故选：A．【点睛】本题考查了正数与负数在实际生活中的应用、有理数的大小比较法则，掌握大小比较法则是解题关键．7．下列有理数最小的是（    ）A． B． C．0 D．1【答案】B【分析】根据正数大于一切负数；两个负数，绝对值大的其值反而小解答即可．【详解】根据正数大于0，0大于负数，故排除C、D两项，
两个负数比较大小，绝对值大的数值反而小，
∵，∴，
∴最小的数是.
故选：B．【点睛】本题考查了有理数的大小比较，非常简单，要注意：①正数都大于0；②负数都小于0；③正数大于一切负数；④两个负数，绝对值大的其值反而小；先分类比较，再判断两个负数的大小．8．在﹣4，2，0，﹣3这四个数中，最小的数是（　　）A．﹣4 B．2 C．0 D．﹣3【答案】A【分析】根据正数大于0，0大于负数，正数大于负数进行比较即可．【详解】解：根据有理数比较大小的方法，可得﹣4＜﹣3＜0＜2，∴在﹣4，2，0，﹣3这四个数中最小的数是﹣4．故选A．【点睛】本题主要考查的是比较有理数的大小，掌握比较有理数大小的法则是解题的关键.  二、填空题9．比较大小：______（填“”，“”或“”）；用种方法说明你是怎么比较的．【答案】；见解析．【分析】（1）根据与的差的正负，判断出它们的大小关系即可；（2）两个负数，绝对值大的其值反而小，据此判断即可．【详解】解：①，；②，，，．故答案为：．【点睛】本题考查了有理数大小比较的方法，要熟练掌握，解答此题的关键是要明确：①正数都大于；②负数都小于；③正数大于一切负数；④两个负数相比较，绝对值大的反而小．10．比较大小：  － ______－（填“＜”或“＞”）【答案】【分析】根据绝对值大的反而小的方法进行比较.【详解】∵＞，∴－ <－.故答案是：<.【点睛】考查了比较两个负数的大小，解题关键是运用了绝对值大的反而小的方法进行比较.11．大于-3．5小于4．7的整数有_______个．【答案】8【解析】试题分析：根据有理数的大小比较及有理数的分类即可得到结果.大于-3．5小于4．7的整数有-3、-2、-1、0、1、2、3、4共8个.考点：有理数的大小比较，有理数的分类点评：本题是有理数的分类的基础应用题，在中考中比较常见，常以填空题、选择题形式出现，难度一般.12．比较大小：_______．【答案】 ＜【详解】试题分析：两个负数比较因为绝对值大的反而小，所以只需要比较绝对值即可.，因为所以 考点：有理数的比较.13．大于﹣7小于6.5的正整数有_____个．【答案】6【分析】根据正整数的含义及利用数轴进行有理数的大小比较可得答案．【详解】解：如图：所以大于﹣7小于6.5的正整数有1，2，3，4，5，6，一共6个．故答案为：6．【点睛】本题考查的是正整数的含义及利用数轴进行有理数的大小比较，掌握正整数的含义与有理数的大小比较是解题的关键．14．比较大小:-(-0.3)___(填“=”“>”或“<”).【答案】<【详解】分析：根据有理数计算法则求出两个数，然后根据有理数的大小比较方法得出答案．详解：∵－(－0.3)=0.3，， 0.3＜，  ∴－(－0.3)＜．点睛：本题主要考查的是有理数的大小比较方法，属于基础题型．两个正数比较大小，绝对值大的数就大．15．比较大小：-2020____________-2021（填“>”，“<”或“=”）．【答案】＞【分析】比较两个负数，绝对值大的反而小，据此回答即可．【详解】解：∵|-2020|=2020，|-2021|=2021，2020<2021，∴-2020＞-2021，故答案为：＞．【点睛】本题考查有理数的大小比较，侧重比较两个负数，依据法则是解答本题的关键．16．比较大小： ____ （用“>”、“<”号填空 ）．【答案】>【解析】∵，∴，即“空格处应填>”.考点：有理数大小的比较，两个负数绝对值大的反而小. 三、解答题17．画一条数轴，把下列各数在数轴上表示出来，并用“＜”把它们连接起来．             －4，  3.5，  0，， 2【答案】-4＜＜0＜2＜3.5【解析】【分析】根据数轴是表示数的一条直线，可把数在数轴上表示出来，根据数轴上的点表示的数右边的总比左边的大，可得答案；【详解】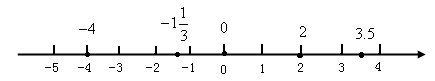-4＜＜0＜2＜3.5．【点睛】本题考查了有理数大小比较，数轴上的点表示的数右边的总比左边的大．18．比较-3与2的大小．【答案】-3<2【解析】试题分析：有理数的大小比较法则：正数大于0，负数小于0，正数大于负数，两个负数，绝对值大的反而小.考点：有理数的大小比较点评：本题是有理数的大小比较的基础应用题，在中考中比较常见，一般以选择题、填空题形式出现，属于基础题，难度不大.19．比较下列各组数的大小：(1)和；(2)－2.8和－3.7.【答案】(1) ＞ ;(2) －2.8＞－3.7.【解析】【分析】根据两个负数比较大小，其绝对值大的反而小比较即可.【详解】解：(1)因为，，＜，所以＞.(2)因为|－2.8|＝2.8，|－3.7|＝3.7,2.8＜3.7，所以－2.8＞－3.7.【点睛】本题考查了对有理数的大小比较法则的应用.注意：正数都大于0，负数都小于0，正数大于负数，两个负数比较大小，其绝对值大的反而小.20．若，且，分别求的值.【答案】x=2，y=5或x=-2，y=5【分析】先根据求出x=±2，y=±5，在根据确定x、y的值．【详解】∵∴x=±2，y=±5又∵∴x=2，y=5或x=-2，y=5【点睛】本题考查的是绝对值的意义，掌握绝对值的定义及有理数的大小比较是关键．21．在数轴上表示下列各数，并比较大小．2，－，0，，－1.5.【答案】画数轴略，－1.5＜－＜0＜＜2.【解析】分析：根据数轴表示数的方法表示出所给的5个数，然后利用数轴上的点从左到右的顺序，就是点所表示的数从小到大的顺序，写出它们的大小关系．详解：用数轴表示为：∵数轴上的点从左到右的顺序，就是点所表示的数从小到大的顺序，∴－1.5＜－＜0＜＜2点睛：考查了利用数轴来比较有理数的大小，先在数轴上找出数所对应的点，再利用数轴上的点从左到右的顺序，就是点所表示的数从小到大的顺序来比较数的大小.22．在数轴上表示，，，并把这些数的相反数用“＜”连接起来.【答案】【分析】首先计算出每个算式的值，把这些数在数轴上表示出来；再根据相反数的定义求得每个数的相反数，最后借助数轴上右边的数大于左边的数即可得解.【详解】解：，，，-1，-2，-4在数轴上表示如图所示.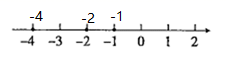它们的相反数用“＜”连接为：.故答案为.【点睛】本题考查相反数，有理数大小比较，重点是确定数值在坐标原点的左侧还是右侧，负数在原点左侧，正数在原点右侧．23．比较下列各组数的大小：（写出过程）  （1）与；       （2）与．【答案】（1）；（2）【分析】（1）根据有理数的大小比较求解即可；（2）先对原数化简，然后利用有理数的大小比较求解即可．【详解】解：（1），，∵   ，∴   ．（2）∵   ，，∴   ．【点睛】本题主要考查有理数的大小比较，熟练掌握有理数的大小比较是解题的关键．24．在数轴上表示出以下各数，并把这些数由小到大用“＜”号连接起来．【答案】如图所示见解析，.【分析】先将各个数标注在数轴上，再根据数轴方向向右时，右边的数总比左边的大排列.【详解】解：＝﹣1，|﹣2|＝2，在数轴上表示为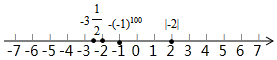：按从小到大的顺序排列为：．【点睛】本题考查了利用数轴比较有理数的大小，关键是掌握当数轴方向向右时，右边的数总比左边的大.25．小贝认为：若有理数a，b满足，则．小贝的观点正确吗？请说明理由．【答案】小贝的观点不正确．理由见解析．【分析】根据绝对值的含义和求法，可得：两个负数，绝对值小的，这个数反而大；一个正数一个负数，绝对值大的负数小于正数；并举例子证明即可．【详解】解：小贝的观点不正确．理由如下：因为当时，，但是，所以若，则不一定成立，所以小贝的观点不正确．【点睛】此题主要考查了绝对值的含义和应用，要熟练掌握，解答此题的关键是要明确：①当a是正有理数时，a的绝对值是它本身a；②当a是负有理数时，a的绝对值是它的相反数-a；③当a是零时，a的绝对值是零．26．如果，且，求的值．【答案】3或11【分析】先由和得到，再分和进行计算即可得到答案.【详解】因为，所以，因为，所以；当时，；当时，；故或13.【点睛】本题考查绝对值、有理数大小的比较和有理数的加法，解题的关键是掌握求绝对值、有理数大小的比较和有理数的加法.