


高中数学人教A版 (2019)必修 第一册3.1 函数的概念及其表示精品教学设计
展开![]() 3.1函数的概念及其表示(第四课时)教学设计
3.1函数的概念及其表示(第四课时)教学设计
一、内容及内容解析
(一)教学内容
1.选择恰当的方法表示函数;
2.分段函数的应用;
(二)教学内容解析
学生在上一节课已经了解了函数的三种表示及认识了分段函数,本节课通过在实际情景中,学生选择适当的方法表示函数,了解简单的分段函数,提升学生的数学抽象,数学建模素养。在实际问题中,选择恰当的方法表示函数,不仅是应用函数模型解决实际问题的需要,而且是进一步理解函数概念,深化对具体函数模型的认识需要。同时,基于现实生活中分段函数的应用很广泛,因此学习简单的分段函数也是培养学生数学建模素养的重要过程。
(三)教学重点
1.在实际情景中,根据不同的需要选择恰当的方法表示函数;
2.了解简单的分段函数;
二、教学目标
1.通过研究实例,能根据不同的需要选择恰当的方法表示函数,发展数学建模的素养.
2.通过具体实例,能简单应用分段函数,体会利用图象简化代数运算的过程.
三、教学问题诊断分析
问题:对于一个函数问题,如何选择恰当的方法表示问题中的函数关系?
突破:通过课本的例7,引导学生用不同的方法分析三位同学的数学学习情况,再师生一起进行评价并总结。
四、教学支持条件
为了增加学生对函数的理解,可以利用GGB软件,作出图像,让学生观察.
五、教学过程设计
上一节我们已经学习过了函数的三种表示法,那么函数的具体表示方法有哪些呢,在不同的情境中应该选择哪种方法表示呢?
问题1:下面这个例子表示函数用的是什么方法?
例7 表3.1-4是某校高一(1)班三名同学在高一学年度六次数学测试的成绩及班级平均分表.
请你对这三位同学在高一学年的数学学习情况做一个分析.
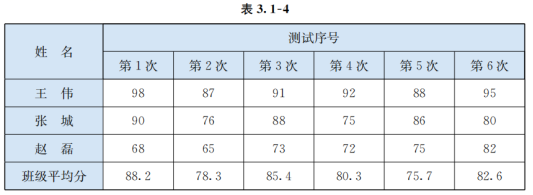
师生活动:(1)教师提出问题,学生分组讨论后回答,根据学生的解答,教师进行必要的补充.
(2)追问1:用上面的方法表示这三位同学的成绩有什么优缺点?
师生活动:教师提出问题,学生分组讨论后回答,根据学生的解答,教师进行必要的补充.
从表中可以读取出每位同学在每次测试中的成绩,但不太容易分析每位同学的成绩变化情况。
(3)追问2:有没有更好的方法能够直观地看到每位同学成绩变化的情况?
师生活动:学生分组讨论后作答,根据学生的解答,教师进行必要的补充.
如果将每位同学的“成绩”与“测试序号”之间的函数关系分别用图象(均为6个离散的点)表示出来,如图,那么就能直观地看到每位同学成绩变化的情况.
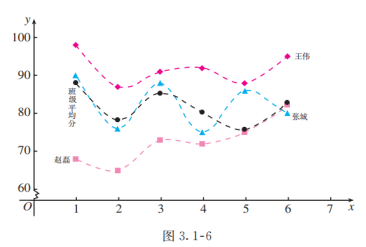
(4)追问3:你能否说说这个方法表示的好处?
师生活动:教师提出问题,学生分组讨论后作答,根据学生的解答,教师进行必要的补充.
从图可以看到,王伟同学的数学学习成绩始终高于班级平均水平,学习情况比较稳定而且成绩优秀.张城同学的数学学习成绩不稳定,总是在班级平均水平上下波动,而且波动幅度较大.赵磊同学的数学学习成绩低于班级平均水平,但表示他成绩变化的图象呈上升趋势,表明他的数学成绩在稳步提高.
设计意图:通过选择恰当的方法表示实际情景中的函数,分析其优劣,引导学生关注选择恰当方法表示函数的重要性。
(5)追问4:图中用虚线连接离散的点,虚线是函数图像的一部分吗?
师生活动:教师提出问题,学生讨论后作答。根据学生的解答,教师进行必要的补充.
图中的虚线不是函数图象的组成部分,之所以用虚线连接同一个函数的散点图,主要是为了让三个函数的图象具有整体性,这样方便比较.
问题2:你能否运用所学解决下面的问题?
例8依法纳税是每个公民应尽的义务,个人取得的所得应依照 《中华人民共和国个人所得税法》向国家缴纳个人所得税 (简称个税).2019年1月1日起,个税税额根据应纳税所得额、税率和速算扣除数确定,计算公式为
个税税额=应纳税所得额×税率-速算扣除数.①
应纳税所得额的计算公式为
应纳税所得额=综合所得收入额-基本减除费用-专项扣除
-专项附加扣除-依法确定的其他扣除.②
其中,“基本减除费用”(免征额)为每年60000元.税率与速算扣除数见表2.
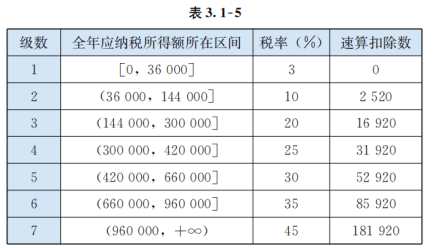
(1)设全年应纳税所得额为t,应缴纳个税税额为y,求y=f(t);
师生活动:(1)学生思考后写出详细解答过程并展示。师生评价并补充。
解:(1)根据表,可得函数y=f(t)的解析式为
y=③
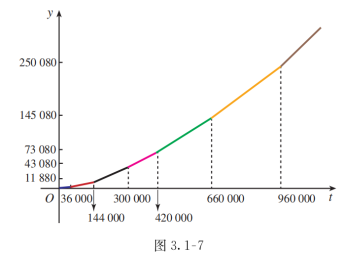
追问1:你能否画出图象?
师生活动:(1)学生独立思考后画出图像。
函数图象如图所示.
(2)追问2:小王全年综合所得收入额为189600元,假定缴纳的基本养老保险、基本医疗保险、失业保险等社会保险费和住房公积金占综合所得收入额的比例分别是8%,2%,1%,9%,专项附加扣除是52800元,依法确定的其他扣除是4560元,那么他全年应缴纳多少综合所得个税?
师生活动:学生思考后详细写出解题过程并展示.教师根据学生的答案进行评价纠错。
根据②,小王全年应纳税所得额为
t=189600-60000-189600(8%+2%+1%+9%)-52800-4560
=0.8×189600-117360
=34320.
将t的值代入③,得y=0.03×34320=1029.6.
所以,小王应缴纳的综合所得个税税额为1029.6元.
设计意图:例8的设计有三个目的:一是不仅可以让学生尝试用函数模型去表达实际问题,培养用数学的眼光观察、分析并解决身边问题的能力,而且渗透了公民意识教育;二是可以更进一步地体会根据问题的特点恰当选择函数的的表示法;三是进一步学习分段函数的表示,让学生体会分段函数在实际中的应用价值。
问题3:请同学们总结一下,本节课我们学习了哪些知识,掌握了哪些方法?
师生活动:老师可以提问同学作答,本节课学习了选择恰当的方法表示实际情景中的函数。
设计意图:通过回顾本节课内容,形成知识体系,进行知识内化。
六、目标检测设计
课堂检测
1.某种产品每件定价80元,每天可售出30件,如果每件定价120元,则每天可售出20件,如果售出件数是定价的一次函数,则这个函数解析式为( )
A.y=-![]() x+50(0<x<200)
x+50(0<x<200)
B.y=![]() x+50(0<x<100)
x+50(0<x<100)
C.y=-![]() x+50(0<x<100)
x+50(0<x<100)
D.y=![]() x+50(0<x<200)
x+50(0<x<200)
2.电讯资费调整后,市话费标准为:通话时间不超过3分钟收费0.2元;超过3分钟后,每增加1分钟收费0.1元,不足1分钟按1分钟计费.通话收费S(元)与通话时间t(分钟)的函数图像可表示为下图中的( )
A.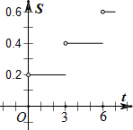 B.
B.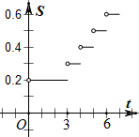
C. D.
D.
3.从甲城市到乙城市t min的电话费由函数g(t)=1.06×(0.75[t]+1)给出,其中t>0,[t]为t的整数部分,则从甲城市到乙城市5.5 min的电话费为( )
A.5.04元 B.5.56元
C.5.84元 D.5.38元
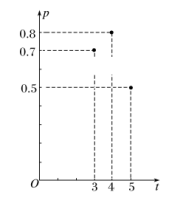
4.加工爆米花时,爆开且不糊的粒数占加工总粒数的百分比称为“可食用率”.在特定条件下,可食用率p与加工时间t(单位:分钟)满足函数关系![]() (a,b,c是常数),如图记录了三次实验的数据.根据上述函数模型和实验数据,可以得到最佳加工时间为________分钟.
(a,b,c是常数),如图记录了三次实验的数据.根据上述函数模型和实验数据,可以得到最佳加工时间为________分钟.
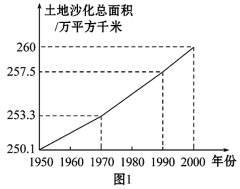
5.在未实行大规模绿化造林之前,我国是世界上受荒漠化危害最严重的国家之一,如图1表示我国土地沙化总面积在1950-2000年的变化情况,由图1中的相关信息,试将上述有关年份中,我国从1950-1970、1970-1990、1990-2000年的平均土地沙化面积在图2中表示出来.

课后作业
教科书第72页练习1,2
设计意图:巩固本节课的主要知识、方法。
人教A版 (2019)必修 第一册4.3 对数优秀教案设计: 这是一份人教A版 (2019)必修 第一册4.3 对数优秀教案设计,共4页。
高中数学人教A版 (2019)必修 第一册4.3 对数公开课教案及反思: 这是一份高中数学人教A版 (2019)必修 第一册4.3 对数公开课教案及反思,共2页。教案主要包含了内容和内容解析,目标及其解析,教学问题诊断分析,教学支持条件分析,课时分配设计等内容,欢迎下载使用。
数学必修 第一册3.1 函数的概念及其表示优秀教学设计: 这是一份数学必修 第一册3.1 函数的概念及其表示优秀教学设计,共4页。教案主要包含了内容及内容解析,教学目标,教学问题诊断分析,教学支持条件,教学过程设计等内容,欢迎下载使用。













