高中数学人教A版 (2019)必修 第一册第一章 集合与常用逻辑用语1.3 集合的基本运算优质教案设计

1.3.1集合的基本运算(1)课时教学设计

一、课题：集合的基本运算（1）

二、教学内容

1.集合并集的含义与运算；

2.集合交集的含义与运算；

3.区分交、并运算的运算符号，会进行简单的离散型和连续型集合的交、并运算.

三、教学目标

  学生能通过类比实数运算，结合具体实例，能理解集合并集、交集运算的含义，掌握简单的集合运算，并学会使用图、数轴等几何方法表达集合的关系及运算，体会直观图示对理解抽象概念的作用，从而体会数形结合在理解集合中的重要作用，发展学生数学运算的核心素养.

四、教学重难点

教学重点：理解并集、交集的含义，并会进行简单的集合基本运算.

教学难点：区分交、并集运算符号，掌握集合的交、并运算.

五、教学设计过程

问题1：我们知道，实数有加法运算，两个实数可以相加，集合是否也有类似的运算呢？请同学们考察下列两组集合，你能说出集合与集合之间的关系吗?

(1)

(2

师生活动：引导学生通过观察集合，并借助图得出集合间的关系，并发现集合的元素全部由集合构成，并且没有元素不属于集合.

设计意图：学生通过观察具体集合，发现集合并集的运算实质，获得数学活动经验，回顾上节知识的同时也回顾了数形结合解决问题的思想.

追问：你能用集合的语言描述集合与集合之间的关系吗？

师生活动：学生尝试将自然语言转化为集合语言，老师进行必要的指导和补充.

 设计意图：让学生学会用数学的语言来描述数学问题，获得概念的严谨表述.

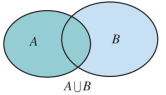并集概念：一般地，由所有属于集合或集合的元素组成的集合. 称为集合与的并集，记作：；读作“并”.用描述法表示为.

图表示为：

例1：设，求.

解：.

设计意图：通过具体例题，深化并集概念，练习离散集合的并集运算.

例2：设集合，集合，求.

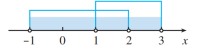解：用数轴表示：

则

追问：若中间两个虚点变为实点后结果改变了吗？ 

师生活动：学生思考后回答.

设计意图：让学生做题时注意把握细节，并体会集合端点对集合并集结果的影响.

问题2：下列关系式成立吗？

师生活动：学生根据并集的概念思考后易得到答案.

设计意图：让学生体会特殊集合的并集运算，考虑问题中特殊情况的处理.

追问：若则？

师生活动：可以引导学生借助图来理解和解决问题.

设计意图：在问题2的基础上，继续让学生进一步理解并集概念，了解集合间的关系与集合运算的联系，并学会用图来直观的研究问题.

问题3：考察下面的问题，集合与集合之间有什么关系？

（1）

（2）

师生活动：学生观察两组集合，发现集合中的元素是由集合中共有的元素组成的，引导学生注意并且不能有漏掉的.如果学生总结不严谨，可以给出集合是立德中学今年在校的身高超过的高一年级女同学，通过比较与的不同点，来引导、帮助学生更加严谨地归纳总结交集的概念，强调是集合的所有元素组成.

设计意图：通过给出两个实例，让学生们自己观察并交流，找出集合A，B与集合C之间的关系，通过模仿上面并集的概念，锻炼了学生观察、类比以及总结的能力. 

交集概念：一般地，由属于集合.用描述法表示为：

用图表示为：

例3：立德中学开运动会，设

解:就是立德中学高一年级中既参加的同学组成的集合.所以，

是立德中学高一年级既参加百米赛跑又参加跳高比赛的同学.

例4：设平面内直线上点的集合为，直线上点的集合为，试用集合的运算表示和的位置关系.解：平面内直线和可能有三种位置关系，即相交于一点，平行或重合.（1）直线和相交于一点P，可表示为；（2）直线和平行可表示为；（3）直线和重合可表示为.

设计意图：学生通过应用交集运算解决实际问题和几何问题，巩固了对交集概念的理解，实现了交集运算的实际应用，同时也考察了学生分类讨论的能力.

问题4：下列交集运算的结果是什么呢？（1）（2）（3）若，则？

师生活动：学生借助图，思考讨论后给出答案.

设计意图：让学生在问题2和交集概念的基础上，类比并集的概念，加强概念横向间的联系.

问题5：请同学们对比交集和并集的概念，从文字上面能发现什么不同吗？

师生活动：学生指出交集中使用的是“且”字，并集中使用的是“或”字.

设计意图：让学生对比交集和并集的概念，加强概念横向间的对比.

追问：如果我们称大于3或大于5的实数为集合，那么3是集合的元素吗？5呢？6呢？这三个元素有什么不同呢？

师生活动：学生经讨论后发现，3不是集合的元素，5和6是集合的元素，其中3不满足大于3也不满足大于5,5只满足其中第一个，6两个都满足。

设计意图：让学生进一步理解或的含义，只要元素属于其中一个集合，即属于并集.

追问：交集的符号是，并集的符号是，交集概念中用且，并集概念中用或，你能区分两者的符号吗？

师生活动：引导学生观察 “”和“且”轮廓的相似，加强记忆，也可以鼓励学生自己找到记忆方法。

设计意图：让学生注意区分交集和并集的符号异同，记忆交集和并集的符号.

六、课堂检测与评价

1.设是小于9的正整数}，求.

2. 已知集合

设计意图：让学生及时巩固所学，检测离散型和连续型两类集合基本运算的掌握情况.

1.3.2集合的基本运算(2)课时教学设计

一、课题：集合的基本运算（2）

二、教学内容

1.在具体情境中，理解全集的含义；

2.理解补集的含义，会求给定子集的补集；

3.能进行简单的集合混合运算.

三、教学目标

  在学习了交集和并集运算的基础上，学生能通过类比实数减法运算，结合具体实例，能理解集合全集和补集运算的含义，掌握简单的补集运算，并学会使用图、数轴等几何方法表达全集和补集运算，进一步体会直观图示对理解抽象概念的作用，从而体会数形结合在理解集合中的重要作用，发展学生数学运算的核心素养.

四、教学重难点

教学重点：理解全集和补集的含义，并会进行简单的集合补集运算.

教学难点：正确理解全集的含义，能够进行集合的混合运算.

五、教学设计过程

引言：在上一节中，我们通过类比实数的加法运算，学习了集合的并集运算，并在并集的基础上学习了交集运算，请同学们完成下题：若集合，，求、。

师生活动：学生完成题目，过程中老师注意指出学生问题。

设计意图：学生复习已有知识，为本节学习全集和补集热身.

问题1：在实数范围内解方程，方程的解是什么？若在自然数范围呢？两者有什么不同？

师生活动：引导学生观察两个方程解的不同是由于研究问题的框定范围不同导致的，发现确定研究范围的重要性。

设计意图：学生通过观察具体问题，体会研究问题的范围对结果的重要性。

全集概念：一般地，如果一个集合含有我们所研究问题中所涉及的所有元素，那么就称这个集合为全集（universe set），通常记作.

图一般用矩形表示为：

需要指出的是：全集并不是固定不变的，在具体的研究问题中全集是具体的，一般情况下我们把作为全集，特定情况下也可以给定全集，比如在自然数范围内解方程，全集就是自然数。

问题2：我们知道，实数有减法运算，比如，9中去掉6剩下的部分就是3，当然我们也可以说9中去掉3剩下的部分就是6，集合是否也有类似的运算呢？请同学们考察下列两组集合，你能说出全集中去掉集合的元素剩下元素组成的集合，与集合之间的关系吗?

(1)

(2

师生活动：引导学生通过观察集合，并借助图得出集合间的关系，并发现全集中去掉集合的元素剩下元素组成的集合就是集合，同理全集中去掉集合的元素剩下元素组成的集合就是集合。

设计意图：学生通过观察具体集合，对比实数减法运算，发现补集的运算实质，获得数学活动经验.

追问：你能计算一下吗？

师生活动：学生计算得到, ,并用自然语言指出两者关系。

设计意图：让学生进一步用数学语言描述给定集合与其补集的集合关系，并用自然语言理解.

补集概念：对于全集的一个子集，由全集中所有不属于集合的所有元素组成的集合称为集合相对于全集的补集（complementary set）,简称为集合的补集，记作,即 .

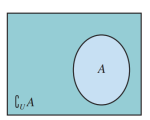
图表示为：

注意：补集是相对于全集而言的，不可单独出现。

问题3：下列关系式成立吗？（），（），

师生活动：学生根据补集的概念，借助图思考后易得到上述式子是正确的.

设计意图：让学生掌握集合与的关系，理解与互为补集关系.

追问： ？？

师生活动：学生根据补集和空集概念得到.

设计意图：可以引导学生注意空集的特殊性，进一步理解补集.

例5：设，求，.

解:，，

设计意图：通过具体例题，深化补集概念，练习离散集合的补集运算.

例6：已知集合.

解:借助图可得，.

设计意图：通过具体例题，深化补集概念，练习连续集合的补集运算.

例7：已知集合

解:借助图可得，，,.

设计意图：通过具体例题，使学生掌握集合的交并补的混合运算.

例8：设全集，求，.

解：根据三角形的分类可知

设计意图：学生通过应用补集运算表示几何关系，巩固了对补集概念的理解。

六、课堂检测与评价

1.设是小于9的正整数}，求.

2. 设S={|是至少有一组对边平行的四边形}，|是平行四边形}，B={|是菱形}，C={|是矩形}，求.

3. 已知集合

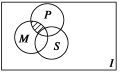4.如图，是全集是的个子集，则阴影部分所表示的集合是（    ）

设计意图：让学生及时巩固所学，检测集合基本运算的掌握情况，重点检测对补集运算的理解.