
【同步教案】北师大版数学七年级上册--4.5多边形和圆的初步认识 教案
展开4.5 多边形和圆的初步认识
一、教学目标
(1)在具体情境中认识多边形、正多边形、圆、扇形;
(2)能根据扇形和圆的关系求扇形的圆心角的度数。
二、课时安排
1课时
三、教学重点
认识多边形、正多边形、圆、扇形,能根据扇形和圆的关系求扇形的圆心角的度数。
四、教学难点
探索分割平面图形的一些规律,感受图形世界的丰富图形,养成把数学应用于生活实际问题的习惯
五、教学过程
(一)情境导入
1、有哪些熟悉的平面图形?



(二)讲授新课
1、多边形和对角线
三角形、四边形、五边形、六边形等都是多边形,它们都是由若干条不在同一直线上的线段首位顺次相连组成的封闭平面图形。
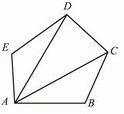
如图,在多边形ABCDE中,点A、B、C、D、E是多边形的顶点;线段AB、BC、CD、DE、EA是多边形的边;∠EAB、∠ABC、∠BCD、∠CDE、∠DEA是多边形的内角;AC、AD都是连接不相邻两个顶点的线段,像这样的线段叫做多边形的对角线。
我们看一下多边形的表格,看看能发现什么规律。
多边形 | 四边形 | 五边形 | 六边形 | n边形 |
图形 |
|
|
|
|
从一个顶点发出 的对角线的条数 | 1条 | 2条 | 3条 | (n-3)条 |
分成三角 形的个数 | 2个 | 3个 | 4个 | (n-2)个 |
内角和 | 360° | 540° | 720° | (n-2)×180° |
2、观察下图中的多边形,它们的边、角有什么特点?

各边相等,各角也相等的多边形叫做正多边形。上图中的多边形分别是正三角形、正四边形(正方形)、正五边形、正六边形、正八边形。
3、下边图形中有我们熟悉的圆和扇形,你还记得用那些方法可以画一个圆吗?你能用一根细绳和笔画出一个圆吗?

平面上,一条线段绕着它固定的一个端点旋转一周,另一个端点形成的图形叫做圆。固定的端点O称为圆心,线段OA称为半径。
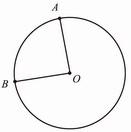
圆上任意两点A、B间的部分叫做圆弧,简称弧,记作![]() ,读作“圆弧”或弧AB;由一条弧AB和经过这条弧的端点的两条半径OA、OB组成的图形叫做扇形;顶点在圆心的角叫做圆心角。
,读作“圆弧”或弧AB;由一条弧AB和经过这条弧的端点的两条半径OA、OB组成的图形叫做扇形;顶点在圆心的角叫做圆心角。
例 将一个圆分割成三个扇形,它们的圆心角的度数比为1:2:3:4,求这三个扇形的圆心角的度数。
解:因为一个圆周角为360°,所以分成的三个扇形的圆心角分别是:
![]() ,
,![]() ,
,![]()
(三)重难点精讲
正确认识角的平分线
(四)归纳小结
1、多边形和对角线
2、正多边形
3、圆弧、圆心角
(五)随堂检测
1、将一个圆分割成四个大小相同的扇形,则每个扇形的圆心角是________度.
2、如果一个圆的面积是30 cm2,那么其中圆心角为60°的扇形面积是________cm2.
3、一个正八边形的边长是2 cm,则这个正八边形的周长是________cm.
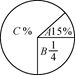
4、如图,将圆分成A、B、C三个扇形,且半径为3 cm.
(1)求扇形C的面积;
(2)求扇形A和B圆心角的度数.
六、板书设计
4.5 多边形和圆的初步认识
概念 例题 练习
七、作业布置
1.家庭作业:完成本节课的同步练习;
2.预习作业:完成导学案5.1《认识一元一次方程》探究案









