初中湘教版3.2 平行线分线段成比例优秀练习题

3.2 平行线分段成比例

班级：___________姓名：___________得分：__________

一．选择题

1．如图，DE∥FG∥BC，若DB=4FB，则EG与GC的关系是（　　）

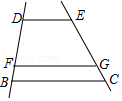
A．EG=4GC   B．EG=3GC   C．EG=GC   D．EG=2GC

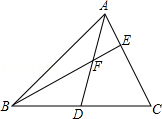
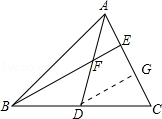
2．如图，AG：GD=4：1，BD：DC=2：3，则AE：EC的值是（　　）

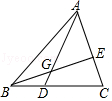
A．3：2      B．4：3           C．6：5     D．8：5

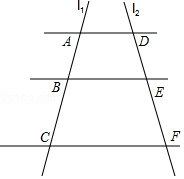
3．如图，已知直线l1，l2，l3分别交直线l4于点A，B，C，交直线l5于点D，E，F，且l1∥l2∥l3，若AB=4，AC=6，DF=9，则DE=（　　）

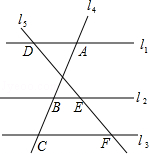
A．5       B．6         C．7    D．8

4．如图，线段AB与CD交于点O，下列条件中能判定AC∥BD的是（　　）

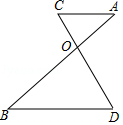
A．OC=1，OD=2，OA=3，OB=4    B．OA=1，AC=2，AB=3，BD=4

C．OC=1，OA=2，CD=3，OB=4    D．OC=1，OA=2，AB=3，CD=4．

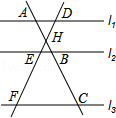
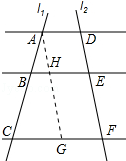
5．如图，直线l1∥l2∥l3，直线AC分别交l1，l2，l3于点A，B，C；直线DF分别交l1，l2，l3于点D、E、F，AC与DF相交于点H，且AH=2，HB=1，BC=5，则=（　　）

A．          B．2        C．      D．

二．填空题

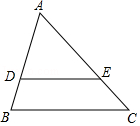
6．如图，在△ABC中，DE∥BC，AD=4，DB=2，AE=6，则EC的长为　   　．

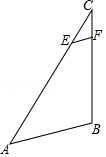
7．如图所示，AB∥EF，若CE=4，CF=3，AE=BC，则BC=　   　．

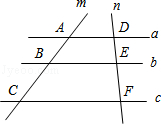
8．如图，直线a∥b∥c，直线m、n与这三条直线分别交于点A、B、C和点D、E、F．若AB=4，BC=6，DE=3，则DF的长为　   　．

三．解答题

9．如图，已知AD∥BE∥CF，它们依次交直线l1、l2于点A、B、C和D、E、F．若=，AC=14，

（1）求AB的长．

（2）如果AD=7，CF=14，求BE的长．

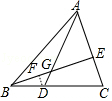
10．如图，AD是△ABC的中线，点E在AC上，BE交AD于点F．某数学兴趣小组在研究这个图形时得到如下结论：

（1）当=时，=；

（2）当=时，=；

（3）当=时，=；

…

猜想：当=时，=？并说明理由．

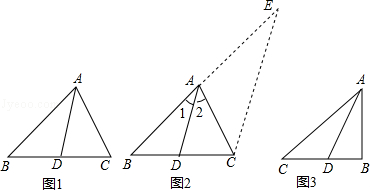
11．阅读与计算，请阅读以下材料，并完成相应的问题．

角平分线分线段成比例定理，如图1，在△ABC中，AD平分∠BAC，则=．下面是这个定理的部分证明过程．

证明：如图2，过C作CE∥DA．交BA的延长线于E．…

任务：

（1）请按照上面的证明思路，写出该证明的剩余部分；

（2）填空：如图3，已知Rt△ABC中，AB=3，BC=4，∠ABC=90°，AD平分∠BAC，则△ABD的周长是　   　．

试题解析

一．选择题

1．B

【分析】根据平行线分线段成比例定理即可得到答案．

【解答】解：∵DE∥FG∥BC，DB=4FB，

∴．

故选：B．

【点评】此题主要考查平行线分线段成比例定理的理解及运用．根据平行线分线段成比例定理解答是解题的关键．

2．D

【分析】过点D作DF∥CA交BE于F，如图，利用平行线分线段成比例定理，由DF∥CE得到==，则CE=DF，由DF∥AE得到===，则AE=4DF，然后计算的值．

【解答】解：过点D作DF∥CA交BE于F，如图，

∵DF∥CE，

∴=，

而BD：DC=2：3，

∴=，则CE=DF，

∵DF∥AE，

∴=，

∵AG：GD=4：1，

∴=，则AE=4DF，

∴==．

故选：D．

【点评】本题考查了平行线分线段成比例：三条平行线截两条直线，所得的对应线段成比例．平行于三角形一边的直线截其他两边（或两边的延长线），所得的对应线段成比例．

3．B

【分析】根据平行线分线段成比例定理解答即可．

【解答】解：∵l1∥l2∥l3，AB=5，AC=8，DF=12，

∴，

即，

可得；DE=6，

故选：B．

【点评】本题考查了平行线分线段成比例定理的应用，能熟练地运用定理进行计算是解此题的关键，题目比较典型，难度适中，注意：对应成比例．

4．C

【分析】根据平行线的判定方法即可一一判断．

【解答】解：A、∵≠，

∴本选项不符合题意．

B、无法判断=，

∴本选项不符合题意；

C、∵OC=1，OA=2，CD=3，OB=4，

∴=，

∴AC∥BD，

∴本选项符合题意；

D、∵≠，

∴本选项不符合题意．

故选：C．

【点评】本题考查平行线分线段成比例定理，平行线的判定等知识，解题的关键是熟练掌握基本知识，所以中考常考题型．

5．A

【分析】求出AB=3，由平行线分线段成比例定理得出比例式，即可得出结果．

【解答】解：∵AH=2，HB=1，

∴AB=AH+BH=3，

∵l1∥l2∥l3，

∴==．

故选：A．

【点评】本题考查了平行线分线段成比例定理；熟记平行线分线段成比例定理是解决问题的关键．

二．填空题

6．3

【分析】根据平行线分线段成比例定理，列出比例式求解即可得到答案．

【解答】解：∵DE∥BC，

∴，

即，

解得：EC=3，

则EC的长是3．

故答案为：3．

【点评】此题考查了平行线分线段成比例定理的运用，熟练利用平行线分线段成比例定理是解题关键．

7．12

【分析】根据平行线分线段成比例解答即可．

【解答】解：∵AB∥EF，

∴=．

∵CE=4，CF=3，AE=BC，

∴=，

则BC=12．

故答案是：12．

【点评】本题考查平行线分线段成比例定理，找准对应关系，避免错选其他答案．

8．7.5

【分析】根据平行线分线段成比例定理得到，代入数据即可得到结论．

【解答】解：∵AD∥BE∥CF，

∴，

即，

∴DF=7.5，

故答案为：7.5

【点评】本题主要考查平行线分线段成比例的性质，掌握平行线分线段可得对应线段成比例是解题的关键．

三．解答题

9．【分析】（1）由平行线分线段成比例定理和比例的性质得出，即可求出AB的长；

（2）过点A作AG∥DF交BE于点H，交CF于点G，得出AD=HE=GF=7，由平行线分线段成比例定理得出比例式求出BH，即可得出结果．

【解答】解：（1）∵AD∥BE∥CF，

∴，

∴，

∵AC=14，

∴AB=4，

（2）过点A作AG∥DF交BE于点H，交CF于点G，如图所示：

又∵AD∥BE∥CF，AD=7，

∴AD=HE=GF=7，

∵CF=14，

∴CG=14﹣7=7，

∵BE∥CF，

∴，

∴BH=2，

∴BE=2+7=9．

【点评】本题考查了平行线分线段成比例：三条平行线截两条直线，所得的对应线段成比例；熟练掌握平行线分线段成比例，通过作辅助线运用平行线分线段成比例求出BH是解决问题的关键．

10．【分析】如图，作辅助线；证明，得到EG=nAE；证明EG=CG，AC=（2n+1）AE，即可解决问题．

【解答】解：猜想：当=时，=；理由如下：

如图，过点D作DG∥BE，交AC与点G；

则，

∴，EG=nAE；

∵AD是△ABC的中线，

∴EG=CG，AC=（2n+1）AE，

∴．

【点评】该题主要考查了平行线分线断成比例定理等几何知识点的性质及其应用问题；解题的关键是作辅助线，构造平行线，灵活运用平行线分线断成比例定理来分析、判断、推理或解答．

11．【分析】（1）如图2，过C作CE∥DA．交BA的延长线于E，利用平行线分线段成比例定理得到=，利用平行线的性质得∠2=∠ACE，∠1=∠E，由∠1=∠2得∠ACE=∠E，所以AE=AC，于是有=；

（2）先利用勾股定理计算出AC=5，再利用（1）中的结论得到=，即=，则可计算出BD=，然后利用勾股定理计算出AD=，从而可得到△ABD的周长．

【解答】（1）证明：如图2，过C作CE∥DA．交BA的延长线于E，

∵CE∥AD，

∴=，∠2=∠ACE，∠1=∠E，

∵∠1=∠2，

∴∠ACE=∠E，

∴AE=AC，

∴=；

（2）解：如图3，∵AB=3，BC=4，∠ABC=90°，

∴AC=5，

∵AD平分∠BAC，

∴=，即=，

∴BD=BC=，

∴AD===，

∴△ABD的周长=+3+=．

故答案为．

【点评】本题考查了平行线分线段成比例定理：三条平行线截两条直线，所得的对应线段成比例．