湘教版九年级上册3.1 比例线段精品精练

3.1.2 成比例线段

班级：___________姓名：___________得分：__________

（满分：100分，考试时间：40分钟）

一．选择题（共5小题，每题8分）

1．下列线段中，能成比例的是（　　）

A．3cm、6cm、8cm、9cm     B．3cm、5cm、6cm、9cm

C．3cm、6cm、7cm、9cm     D．3cm、6cm、9cm、18cm

2．已知线段a=2，b=8，线段c是线段a、b的比例中项，则c=（　　）

A．2    B．±4    C．4    D．8

3．在比例尺为1：38 000的城市交通地图上，某条道路的长为5cm，则它的实际长度为（　　）

A．0.19 km   B．1.9 km   C．19 km   D．190 km

4．黄金分割数是一个很奇妙的数，大量应用于艺术、建筑和统计决策等方面，请你估算﹣1的值（　　）

A．在1.1和1.2之间     B．在1.2和1.3之间

C．在1.3和1.4之间     D．在1.4和1.5之间

5．点C为线段AB的黄金分割点，且AC＞BC，下列说法正确的有（　　）

①AC=AB，②AC=AB，③AB：AC=AC：BC，④AC≈0.618AB

A．1个    B．2个    C．3个    D．4个

二．填空题（共5小题，每题8分）

6．若（a+b+c≠0），则k=　   　．

7．在比例尺为1：200000的城市交通地图上，某条道路的长为17cm，则这条道路的实际长度用科学记数法表示为　   　m．

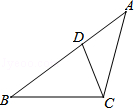
8．如图，D为△ABC的边AB上一点，如果∠ACD=∠ABC时，那么图中　   　是AD和AB的比例中项．

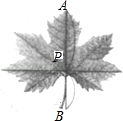
9．大自然是美的设计师，即使是一片小小的树叶，也蕴含着“黄金分割”，如图，P为AB的黄金分割点（AP＞PB），如果AB的长度为10cm，那么PB的长度为　   　cm．

10．已知线段AB=4，点P是线段AB的黄金分割点，且AP＜BP，那么AP的长为　   　．

三．解答题（共3小题，第11、12题各5分，第13题10分）

11．已知线段a=0.3m，b=60cm，c=12dm．

（1）求线段a与线段b的比．

（2）如果线段a、b、c、d成比例，求线段d的长．

（3）b是a和c的比例中项吗？为什么？

12．如图，四边形ABCD与四边形ABFE都是矩形，AB=3，AD=6.5，BF=2．

（1）求下列各线段的比：，，；

（2）指出AB，BC，CF，CD，EF，FB这六条线段中的成比例线段（写一组即可）

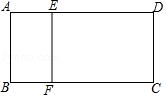
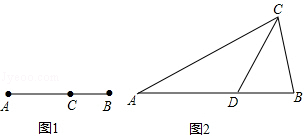
13．如图1，我们已经学过：点C将线段AB分成两部分，如果，那么称点C为线段AB的黄金分割点．某校的数学拓展性课程班，在进行知识拓展时，张老师由黄金分割点拓展到“黄金分割线”，类似地给出“黄金分割线”的定义：直线l将一个面积为S的图形分成两部分，这两部分的面积分别为S1，S2，如果，那么称直线l为该图形的黄金分割线．

如图2，在△ABC中，∠A=36°，AB=AC，∠C的平分线交AB于点D．

（1）证明点D是AB边上的黄金分割点；

（2）证明直线CD是△ABC的黄金分割点．

试题解析

一．选择题

1．D

【分析】如果其中两条线段的乘积等于另外两条线段的乘积，则四条线段叫成比例线段．

【解答】解：根据如果其中两条线段的乘积等于另外两条线段的乘积，则四条线段叫成比例线段．

所给选项中，只有D符合，3×18=6×9，故选D．

【点评】理解成比例线段的概念，注意在线段两两相乘的时候，要让最小的和最大的相乘，另外两条相乘，看它们的积是否相等进行判断．

2．C

【分析】根据比例中项的定义得到c2=ab，然后利用算术平方根的定义求c的值．

【解答】解：∵线段c是线段a、b的比例中项，

∴c2=ab=2×8，

∴c=4．

故选：C．

【点评】本题考查了比例线段：对于四条线段a、b、c、d，如果其中两条线段的比（即它们的长度比）与另两条线段的比相等，如  a：b=c：d（即ad=bc），我们就说这四条线段是成比例线段，简称比例线段．

3．B

【分析】根据比例尺=图上距离：实际距离，依题意列比例式直接求解即可．

【解答】解：设这条道路的实际长度为x，则，

解得x=190000cm=1.9km．

∴这条道路的实际长度为1.9km．

故选：B．

【点评】此题考查比例线段问题，能够根据比例尺正确进行计算，注意单位的转换．

4．B

【分析】根据≈2.236，可得答案．

【解答】解：∵≈2.236，

∴﹣1≈1.236，

故选：B．

【点评】本题考查了估算无理数的大小，利用≈2.236是解题关键．

5．C

【分析】根据黄金分割的概念和黄金比值进行解答即可．

【解答】解：∵点C数线段AB的黄金分割点，

∴AC=AB，①正确；

AC=AB，②错误；

BC：AC=AC：AB，③正确；

AC≈0.618AB，④正确．

故选：C．

【点评】本题考查的是黄金分割的概念，掌握把一条线段分成两部分，使其中较长的线段为全线段与较短线段的比例中项，这样的线段分割叫做黄金分割，他们的比值叫做黄金比是解题的关键．

二．填空题

6．2

【分析】去掉分母，然后整理求解即可．

【解答】解：∵===k，

∴a+b=ck，b+c=ak，c+a=bk，

∴（a+b）+（b+c）+（c+a）=ck+ak+bk，

∴（a+b+c）k=2（a+b+c），

∵a+b+c≠0，

∴k=2．

故答案为：2．

【点评】本题考查了比例的性质，比较简单，用含k的式子表示出分子是解题的关键．

7．3.4×104

【分析】根据比例尺=图上距离：实际距离，依题意列比例式直接求解即可．

【解答】解：设这条道路的实际长度为x，则，

解得x=3400000cm=3.4×104m．

∴这条道路的实际长度为3.4×104m．

故答案为；3.4×104

【点评】此题考查比例线段问题，能够根据比例尺正确进行计算，注意单位的转换．

8．AC

【分析】根据两角分别相等的两个三角形相似，可得△ACD∽△ABC的关系，根据相似三角形的性质，可得答案．

【解答】解：在△ACD与△ABC中，

∠ACD=∠ABC，∠A=∠A，

∴△ACD∽△ABC，

∴=，

∴AC是AD和AB的比例中项．

故答案为AC．

【点评】本题考查了相似三角形的判定与性质，比例线段，得出△ACD∽△ABC是解题的关键．

9．（15﹣5）

【分析】先利用黄金分割的定义计算出AP，然后计算AB﹣AP即得到PB的长．

【解答】解：∵P为AB的黄金分割点（AP＞PB），

∴AP=AB=×10=5﹣5，

∴PB=AB﹣PA=10﹣（5﹣5）=（15﹣5）cm．

故答案为（15﹣5）．

【点评】本题考查了黄金分割：把线段AB分成两条线段AC和BC（AC＞BC），且使AC是AB和BC的比例中项（即AB：AC=AC：BC），叫做把线段AB黄金分割，点C叫做线段AB的黄金分割点．其中AC=AB≈0.618AB，并且线段AB的黄金分割点有两个．

10．（6﹣2）

【分析】根据黄金分割点的定义和AP＜BP得出PB=AB，代入数据即可得出BP的长度．

【解答】解：由于P为线段AB=4的黄金分割点，

且AP＜BP，

则BP=×4=（2 ﹣2）cm．

∴AP=4﹣BP=6﹣2

故答案为：（6﹣2）cm．

【点评】本题考查了黄金分割．应该识记黄金分割的公式：较短的线段=原线段的 ，较长的线段=原线段的 ．

三．解答题

11．【分析】（1）根据a=0.3m=30cm；b=60cm，即可求得a：b的值；

（2）根据线段a、b、c、d是成比例线段，可得=，再根据c=12dm=120cm，即可得出线段d的长；

（3）根据b2=3600，ac=30×120=3600，可得b2=ac，进而得出b是a和c的比例中项．

【解答】解：（1）∵a=0.3m=30cm；b=60cm，

∴a：b=30：60=1：2；

（2）∵线段a、b、c、d是成比例线段，

∴=，

∵c=12dm=120cm，

∴=，

∴d=240cm；

（3）是，理由：

∵b2=3600，ac=30×120=3600，

∴b2=ac，

∴b是a和c的比例中项．

【点评】本题主要考查了成比例线段，判段四条线段是否成比例，只要把四条线段按大小顺序排列好，判断前两条线段之比与后两条线段之比是否相等即可；求线段之比时，要先统一线段的长度单位．

12．【分析】（1）根据矩形的性质和线段的和差关系得到CD，EF，BC，CF，再代入数据即可求得各线段的比；

（2）根据成比例线段的定义写一组即可求解．

【解答】解：（1）∵四边形ABCD与四边形ABFE都是矩形，AB=3，AD=6.5，BF=2，

∴CD=EF=AB=3，BC=AD=6.5，CF=BC﹣BF=4.5，

∴==，==，=；

（2）成比例线段有=．

【点评】本题考查了矩形的性质，比例线段，解决问题的关键是得到CD，EF，BC，CF的值．

13．【分析】（1）易证△BCD∽△BAC，则有=，再由BC=CD=AD可得=，由此可得D是AB边上的黄金分割点；

（2）设△ABC的边AB上的高为h，则S△ADC=AD•h，S△DBC=DB•h，S△ABC=AB•h，即可得到=，=．由（1）得=，即可知=，由此可得CD是△ABC的黄金分割线．

【解答】解：（1）点D是边AB上的黄金分割点，理由如下：

∵∠A=36°，AB=AC，∴∠B=∠ACB=72°．

∵CD平分∠ACB，∴∠ACD=∠DCB=36°，

∴∠BDC=∠B=72°，∠ACD=∠A=36°，

∴BC=DC=AD．

∵∠A=∠BCD，∠B=∠B，

∴△BCD∽△BAC，

∴=．

∴=．

∴D是AB边上的黄金分割点；

（2）直线CD是△ABC的黄金分割线，理由如下：

设△ABC的边AB上的高为h，则

S△ADC=AD•h，S△DBC=DB•h，S△ABC=AB•h，

∴=，=．

∵D是AB的黄金分割点，

∴=，

∴=．

∴CD是△ABC的黄金分割线．

【点评】本题主要考查了相似三角形的判定与性质、等腰三角形的判定与性质、三角形的面积公式，需要注意的是：当比例顺序不确定时，应分情况讨论，避免出现漏解的现象．