











- 人教版初中数学七年级上册 第二章 整式的加减 章节复习 课件+达标检测(含教师+学生版) 课件 58 次下载
- 人教版初中数学七年级上册 3.1.1 一元一次方程 课件+教案+导学案+分层练习(含教师+学生版) 课件 36 次下载
- 人教版初中数学七年级上册 3.2.1 一元一次方程的解法(一)合并同类项 课件+教案+导学案+分层练习(含教师+学生版) 课件 31 次下载
- 人教版初中数学七年级上册 3.2.2 一元一次方程的解法(一)移项 课件+教案+导学案+分层练习(含教师+学生版) 课件 33 次下载
- 人教版初中数学七年级上册 3.3.1 一元一次方程的解法(二)去括号 课件+教案+导学案+分层练习(含教师+学生版) 课件 30 次下载
初中数学人教版七年级上册3.1.2 等式的性质优秀作业课件ppt
展开3.1.2 等式的性质 分层作业
基础训练
1.若![]() ,则下列变形正确的是( )
,则下列变形正确的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】D
【分析】直接利用等式的基本性质分别判断得出答案;
【详解】A、∵![]() ,故本选项错误,不符合题意;
,故本选项错误,不符合题意;
B、∵![]() ,故本选项错误,不符合题意;
,故本选项错误,不符合题意;
C、∵![]() ,故本选项错误,不符合题意;
,故本选项错误,不符合题意;
D、∵ ![]() ,故本选项正确,符合题意,
,故本选项正确,符合题意,
故选D
【点睛】此题主要考查了等式的性质,正确掌握等式的基本性质是解题关键.
2.下列等式的变形,正确的是( )
A.若![]() ,则
,则![]() B.若
B.若![]() ,则
,则![]()
C.若![]() ,则
,则![]() D.若
D.若![]() ,则
,则![]()
【答案】B
【分析】根据等式的性质依次判断即可.
【详解】解:A、![]() ,当
,当![]() 时,
时,![]() ,选项错误,不符合题意;
,选项错误,不符合题意;
B、![]() ,两边同时减去y得
,两边同时减去y得![]() ,选项正确,符合题意;
,选项正确,符合题意;
C、![]() ,则
,则![]() ,选项错误,不符合题意;
,选项错误,不符合题意;
D、![]() ,当
,当![]() 时,则
时,则![]() ,选项错误,不符合题意;
,选项错误,不符合题意;
故选:B.
【点睛】题目主要考查等式的性质,熟练掌握等式的性质是解题关键.
3.已知![]() ,由等式的性质不能得到的是( )
,由等式的性质不能得到的是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
【答案】B
【分析】根据等式性质逐个计算即可得到答案.
【详解】解:由题意可得,
由![]() 可得,
可得,![]() ,即
,即![]() ,故A不符合题意;
,故A不符合题意;
由![]() 可得,
可得,![]() ,故B符合题意;
,故B符合题意;
由![]() 可得,
可得,![]() ,故C不符合题意;
,故C不符合题意;
由![]() 可得,
可得,![]() ,故D不符合题意;
,故D不符合题意;
故选B.
【点睛】本题考查等式的性质,解题的关键掌握等式的基本性质.
4.下列各式中正确的是( )
A.若![]() ,则
,则![]() B.若
B.若![]() ,则
,则![]()
C.若![]() ,且
,且![]() ,则
,则![]() D.若
D.若![]() ,则
,则![]()
【答案】D
【分析】根据不等式的性质逐项分析判断即可求解.
【详解】解:A. 若![]() ,则
,则![]() ,故该选项不正确,不符合题意;
,故该选项不正确,不符合题意;
B. 若![]() ,则
,则![]() ,故该选项不正确,不符合题意;
,故该选项不正确,不符合题意;
C. 若![]() ,且
,且![]() ,则
,则![]() ,故该选项不正确,不符合题意;
,故该选项不正确,不符合题意;
D. 若![]() ,则
,则![]() ,故该选项正确,符合题意;
,故该选项正确,符合题意;
故选:D.
【点睛】本题考查了不等式的基本性质.不等式的基本性质:不等式两边加(或减)同一个数(或式子),不等号的方向不变;不等式两边乘(或除以)同一个正数,不等号的方向不变;不等式两边乘(或除以)同一个负数,不等号的方向改变.
5.根据等式的性质,下列等式的变形正确的是( )
A.若![]() ,则
,则![]() B.若
B.若![]() ,则
,则![]()
C.若![]() ,则
,则![]() D.若
D.若![]() ,则
,则![]()
【答案】A
【分析】根据等式的性质逐一进行判断即可.
【详解】解:若![]() ,则
,则![]() ,表述正确,故A符合题意;
,表述正确,故A符合题意;
若![]() ,则
,则![]() ,原表述错误,故B不符合题意;
,原表述错误,故B不符合题意;
若![]() ,则
,则![]() 或
或![]() ,原表述错误,故C不符合题意;
,原表述错误,故C不符合题意;
若![]() ,
,![]() ,则
,则![]() ,原表述错误,故D不符合题意;
,原表述错误,故D不符合题意;
故选:A.
【点睛】本题考查了等式的性质,性质1等式两边加同一个数(或式子)结果仍得等式;性质2:等式两边乘同一个数或除以一个不为零的数,结果仍得等式.
6.若![]() ,则下列等式:①
,则下列等式:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;⑤
;⑤![]() .其中正确的有 .(填序号)
.其中正确的有 .(填序号)
【答案】①②④
【分析】根据等式的性质,两边同时加上(减去)同一个数(或式子),等式仍成立;等式两边同时乘(或除以)以同一个数(式子,,不为零,数式子),等式仍成立;由此即可求解.
【详解】解:若![]() ,则下列等式:①
,则下列等式:①![]() ;②
;②![]() ;③
;③![]() ,当
,当![]() 时,分式不成立;④
时,分式不成立;④![]() ;⑤
;⑤![]() ,当
,当![]() 时,分式不成立其中正确的有①②④.
时,分式不成立其中正确的有①②④.
故答案为:①②④.
【点睛】本题主要靠考查等式的性质,掌握等式的加减乘除乘法法则,整式的化简求值是解题的关键.
7.将方程![]() 的两边同时 ,得
的两边同时 ,得![]() ;再将方程
;再将方程![]() 的两边同时 ,得
的两边同时 ,得![]() .
.
【答案】 ![]() /加5 12 12
/加5 12 12 ![]() /除以4 3
/除以4 3
【分析】根据等式的基本性质即可完成解答,等式的基本性质为:1、等式两边同时加上(或减去)同一个整式,等式仍然成立。2、等式两边同时乘或除以同一个不为0的整式,等式仍然成立.
【详解】将方程![]() 的两边同时加5,得
的两边同时加5,得![]() ;再将方程
;再将方程![]() 12的两边同时除以4,得
12的两边同时除以4,得![]() 3.
3.
解:![]()
两边同时![]() 得:
得:![]() ;
;
两边同时![]() 得:
得:![]() ,
,
故答案为:![]() ;
;![]() ;3.
;3.
【点睛】本题主要考查了等式的基本性质,掌握等式的基本性质是解题的关键.
8.在下列各题的横线上填上适当的数或整式,使所得结果仍是等式,并说明根据是等式的哪一条性质以及是怎样变形的.
(1)如果![]() ,那么
,那么![]() ,根据 ;
,根据 ;
(2)如果![]() ,那么
,那么![]() ,根据 ;
,根据 ;
(3)如果![]() ,那么
,那么![]() ,根据 ;
,根据 ;
(4)如果![]() ,那么
,那么![]()
![]() ,根据 .
,根据 .
【答案】 ![]() 等式的性质2,两边都乘
等式的性质2,两边都乘![]()
![]() 等式的性质2,两边都乘
等式的性质2,两边都乘![]() ; 6 等式的性质2,两边都乘
; 6 等式的性质2,两边都乘![]() 3x 等式的性质1,两边都减去3x
3x 等式的性质1,两边都减去3x
【分析】(1)根据等式的性质2:等式的两边同乘(或除以)同一个数(除数不为0)结果仍相等即可得出答案.
(2)根据等式的性质2:等式的两边同乘(或除以)同一个数(除数不为0)结果仍相等即可得出答案.
(3)根据等式的性质2:等式的两边同乘(或除以)同一个数(除数不为0)结果仍相等即可得出答案.
(4)根据等式的性质1:等式的两边加(或减)同一个数(或式子)结果仍相等,即可得出答案.
【详解】解:(1)如果![]() ,那么
,那么![]() ,根据等式的性质2,两边都乘
,根据等式的性质2,两边都乘![]() ;
;
(2)如果![]() ,那么
,那么![]() ,根据等式的性质2,两边都除以
,根据等式的性质2,两边都除以![]() ;
;
(3)如果![]() ,那么
,那么![]() ,等式的性质2,两边都乘
,等式的性质2,两边都乘![]() ;
;
(4)如果![]() ,那么
,那么![]() ,根据等式的性质1,两边都减去3x.
,根据等式的性质1,两边都减去3x.
故答案为:![]() ,等式的性质2,两边都乘
,等式的性质2,两边都乘![]() ;
;![]() ,等式的性质2,两边都乘
,等式的性质2,两边都乘![]() ;6,等式的性质2,两边都乘
;6,等式的性质2,两边都乘![]() ;3x,等式的性质1,两边都减去3x.
;3x,等式的性质1,两边都减去3x.
【点睛】本题考查等式的基本性质.熟练掌握等式的基本性质是解题的关键.
9.给出下列方程的变形:①由![]() ,得
,得![]() ;②由
;②由![]() ,得
,得![]() ;③由
;③由![]() ,得
,得![]() ;④由
;④由![]() ,得
,得![]() .其中正确的有 个.
.其中正确的有 个.
【答案】2
【分析】根据等式的性质逐个判断即可得到答案;
【详解】解:由题意可得,
由![]() ,得
,得![]() ,故①错误,不符合题意;
,故①错误,不符合题意;
由![]() ,得
,得![]() 故②错误,不符合题意;
故②错误,不符合题意;
由![]() ,得
,得![]() 故③正确,符合题意;
故③正确,符合题意;
由![]() ,得
,得![]() ,故④正确,符合题意;
,故④正确,符合题意;
∴正确的有③④,共2个,
故答案为:2
【点睛】本题考查等式性质解一元一次方程的步骤,解题的关键是熟练掌握移项及系数化为1的方法.
10.由![]() ,得
,得![]() ,那么
,那么![]() 应该满足的条件是 .
应该满足的条件是 .
【答案】![]()
【分析】根据等式性质![]() ,等式两边同时乘同一个数,或除以同一个不为
,等式两边同时乘同一个数,或除以同一个不为![]() 的数,结果仍相等,进行解答即可.
的数,结果仍相等,进行解答即可.
【详解】解:根据等式的性质![]() 可得,
可得,
若![]() ,当
,当![]() 时,
时,![]() ,
,
故答案为:![]() .
.
【点睛】本题考查了等式性质,熟练掌握等式的性质并灵活运用是解答本题的关键.
11.如果![]() x-4=6那么2x-12= .
x-4=6那么2x-12= .
【答案】18
【分析】根据等式的性质解答即可.
【详解】解:等式![]() x-4=6的两边都乘3,根据等式的性质2可得2x-12=18.
x-4=6的两边都乘3,根据等式的性质2可得2x-12=18.
故答案为:18.
【点睛】本题考查了等式的性质.解题的关键是掌握等式的性质:性质1、等式两边加同一个数(或式子)结果仍得等式;性质2、等式两边乘同一个数或除以一个不为零的数,结果仍得等式.
12.已知关于x的方程![]() 的解为
的解为![]() ,根据等式的性质,可得
,根据等式的性质,可得![]() 的值为 .
的值为 .
【答案】3
【分析】将![]() 代入方程
代入方程![]() 可得
可得![]() ,然后利用等式的基本性质变形即可求解.
,然后利用等式的基本性质变形即可求解.
【详解】解:已知![]() 的方程
的方程![]() 的解为
的解为![]()
得到:![]() ,
,
根据等式的性质可得:![]() ,
,
则![]() .
.
故答案为:3.
【点睛】本题考查方程的解,等式的基本性质,熟练掌握等式的基本性质是解决问题的关键.
13.已知2a-3b=-3,则4a-6b+5=
【答案】-1
【分析】首先根据题目入手,要求解4a-6b,所以将等式的两边同时乘以2可得4a-6b,代入即可.
【详解】根据等式的性质可得4a-6b=-6
所以4a-6b+5=-6+5=-1.
【点睛】本题主要考查等式的性质,关键在于构造计算的式子.
14.下列方程的变形是否正确?为什么?
(1)由![]() ,得
,得![]() .
.
(2)由![]() ,得
,得![]() .
.
(3)由![]() ,得
,得![]() .
.
(4)由![]() ,得
,得![]() .
.
【答案】(1)不正确,理由见解析
(2)不正确,理由见解析
(3)不正确,理由见解析
(4)不正确,理由见解析
【分析】(1)根据左边减3,右边加3,可得变形不正确;
(2)根据左边除以7,右边乘![]() ,可得变形不正确;
,可得变形不正确;
(3)根据左边乘2,右边加2,可得变形不正确;
(4)根据左边加x减3,右边减x减3,可得变形不正确.
【详解】(1)解:由![]() ,得
,得![]() ,不是
,不是![]() ,故原变形不正确,
,故原变形不正确,
∵方程左边减3,右边加3,
∴变形不正确;
(2)解:由![]() ,得
,得![]() ,不是
,不是![]() ,故原变形不正确,
,故原变形不正确,
∵左边除以7,右边乘![]() ,
,
∴变形不正确;
(3)解:由![]() ,得
,得![]() ,不是
,不是![]() ,故原变形不正确,
,故原变形不正确,
∵左边乘2,右边加2,
∴变形不正确;
(4)解:由![]() ,得
,得![]() ,不是
,不是![]() ,故原变形不正确,
,故原变形不正确,
∵左边加x减3,右边减x减3,
∴变形不正确.
【点睛】本题考查了等式的性质,等式的两边不是都加或都减同一个数,左右大小关系发生了变化,等式的两边不是都乘或都除同一个数(不为0),左右大小关系发生了变化.
15.用等式的性质解下列方程:
(1)![]() ;
;
(2)![]() ;
;
(3)![]() ;
;
(4)![]() .
.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ;(4)
;(4)![]()
【分析】(1)根据等式的性质1:等式的两边同时加上(或减去)同一个数(或字母),等式仍成立,可得答案;
(2)根据等式的两边同时加上(或减去)同一个数(或字母),等式仍成立;等式的两边同时乘以(或除以)同一个不为0数(或字母),等式仍成立;
(3)根据等式的两边同时加上(或减去)同一个数(或字母),等式仍成立;等式的两边同时乘以(或除以)同一个不为0数(或字母),等式仍成立;
(4)根据等式的两边同时加上(或减去)同一个数(或字母),等式仍成立;等式的两边同时乘以(或除以)同一个不为0数(或字母),等式仍成立.
【详解】解:(1)两边都加4,得
![]() ;
;
(2)两边都减2,得
![]() ,
,
两边都乘以2,得
![]() ;
;
(3)两边都减1,得
![]() ,
,
两边都除以3,得
![]() ;
;
(4)两边都加2,得
![]() ,
,
两边都除以4,得
![]() .
.
【点睛】本题主要考查了等式的基本性质,解题的关键是掌握等式的两边同时加上(或减去)同一个数(或字母),等式仍成立;等式的两边同时乘以(或除以)同一个不为0数(或字母),等式仍成立.
16.小周学习《5.2等式的基本性质》后,对等式![]() 进行变形,得出“
进行变形,得出“![]() ”的错误结论,但他找不到错误原因,聪明的你能帮助他找到原因吗?小周同学的具体过程如图所示:
”的错误结论,但他找不到错误原因,聪明的你能帮助他找到原因吗?小周同学的具体过程如图所示:
将等式 得 ∴ |
(1)哪一步等式变形产生错误?
(2)请你分析产生错误的原因.
【答案】(1)第二步等式变形错误
(2)等式两边同时除以一个可能等于零的m
【分析】(1)根据等式的性质可知错误发生在第二步;
(2)根据等式的基本性质即可解答.
【详解】(1)第二步等式变形产生错误.
(2)第二步产生错误的原因是:等式两边同时除以一个可能等于零的![]() ,等式不成立.
,等式不成立.
【点睛】本题考查了等式的基本性质,根据等式的性质是解决本题的关键.
能力提升
17.有三种不同质量的物体“■”“▲”“●”,其中同一种物体的质量都相等.下列四个天平中只有一个天平没有处于平衡状态,则该天平是( )
A.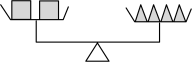 B.
B.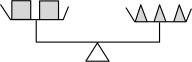
C.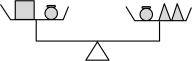 D.
D.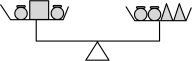
【答案】B
【分析】设“■”的质量为x,“▲”的质量为y “●”的质量为m,列出等式,根据等式的性质计算判断即可.
【详解】设“■”的质量为x,“▲”的质量为y “●”的质量为m,
根据题意,得![]() 即
即![]() ,故A正确,不符合题意;
,故A正确,不符合题意;
∴![]() ,故C正确,不符合题意;
,故C正确,不符合题意;
故B不正确,符合题意;
∴![]() ,故D正确,不符合题意;
,故D正确,不符合题意;
故选B.
【点睛】本题考查了等式的性质,正确理解等式的性质是解题的关键.
18.设“〇”“▱”“△”分别表示三种不同的物体,如图所示,前两架天平保持平衡,如果要使第三架天平也平衡,那么“?”处应放“〇”的个数为( )
![]()
A.5 B.4 C.3 D.2
【答案】D
【分析】设“〇”表示的数为x,“▱”表示的数是y,“△”表示的数为z,根据题意得出![]() ,求出
,求出![]() 即可.
即可.
【详解】解:设“〇”表示的数为x,“▱”表示的数是y,“△”表示的数为z,
根据题意得:![]() ,
,
![]() ,
,
即![]() ,
,
即“?”处应该放“〇”的个数为2,
故选:D.
【点睛】本题考查了等式的性质,能求出![]() 是解此题的关键.
是解此题的关键.
19.如下图可以表示的等式变形是( )(其中![]() 、
、![]() 、
、![]() 均为正数)
均为正数)

A.如果![]() ,那么
,那么![]() B.如果
B.如果![]() ,那么
,那么![]()
C.如果![]() ,那么
,那么![]() D.如果
D.如果![]() ,那么
,那么![]()
【答案】C
【分析】观察图形可得,两边的物品都变为之前的一半,天平仍平衡,结合等式的性质,即可进行解答.
【详解】解:由图可得:两边的物品都变为之前的一半,天平仍平衡,
∴图中可以表示的等式变形是:如果![]() ,那么
,那么![]() ,
,
故选:C.
【点睛】本题主要考查了等式的基本性质,解题的关键是掌握等式的性质一:等式两边同时加上或者是减去同一个整式,等式仍然成立.性质二:等式两边同时乘或除以同一个不为0的整式,等式仍然成立.
20.若![]() ,且
,且![]() ,则
,则![]() .
.
【答案】![]()
【分析】两式相加得![]() ,即可求解.
,即可求解.
【详解】解:∵![]() ①,且
①,且![]() ②,
②,
①+②得:![]()
∴![]()
![]() ,
,
故答案为:![]() .
.
【点睛】本题考查了等式的性质,掌握等式的性质是解题的关键.
21.![]() 、
、![]() 、
、![]() 各代表一个数,根据
各代表一个数,根据![]()
![]()
![]()
![]() ,
,![]()
![]()
![]() =63,
=63,![]()
![]()
![]()
![]() ,求得
,求得![]()
![]()
【答案】![]()
【分析】首先根据![]()
![]()
![]()
![]() ,
,![]()
![]()
![]() =63,判断出
=63,判断出![]() 、
、![]() 的关系;然后根据
的关系;然后根据![]()
![]()
![]()
![]() ,求出
,求出![]() 表示的数是多少即可.
表示的数是多少即可.
【详解】解:![]()
![]()
![]()
![]() ①,
①,![]()
![]()
![]()
![]() ②,
②,
②![]() ①,可得:
①,可得:![]()
![]()
![]()
![]() ,
,
所以![]()
![]()
![]()
![]() ③,
③,
把③代入![]()
![]()
![]()
![]() ,
,
可得:![]()
![]() ,
,
解得:![]()
![]() .
.
故答案为:![]() .
.
【点睛】此题主要考查了简单的等量代换问题,要熟练掌握,解答此题的关键是判断出〇、口的关系.
22.若![]() ,利用等式的性质,比较a与b的大小.
,利用等式的性质,比较a与b的大小.
【答案】![]()
【分析】利用等式的性质将一个字母用另一个字母表示出来,再判断即可.
【详解】解:等式两边同减去![]() ,得:
,得:![]() ,
,
等式两边同减去![]() ,得:
,得:![]() ,
,
等式两边再同时加上1,得:![]() ,
,
∵![]() ,
,
∴![]() .
.
【点睛】本题主要考查了等式的基本性质.等式性质1:等式的两边同时加上或减去同一个数或字母,等式仍成立;等式性质2:等式的两边同时乘以或除以同一个不为0数或字母,等式仍成立,熟练运用等式的性质进行变形是解决本题的关键.
拔高拓展
23.已知x2-xy=-3,2xy-y2=-8,求代数式2x2+4xy-3y2的值.
【答案】-30.
【分析】根据已知式子的特点以及等式的性质,对式子进行变形,进而整体代入求得代数式的值.
【详解】由x2-xy=-3,得2x2-2xy=-6①;
由2xy-y2=-8,得6xy-3y2=-24②.
①+②,得(2x2-2xy)+(6xy-3y2)=(-6)+(-24)=-30,
即2x2+4xy-3y2=-30.
【点睛】本题考查了等式的性质,代数式求值,根据等式的性质对式子进行变形是解题的关键.
数学五年级上册5 简易方程2 解简易方程等式的性质精品课件ppt: 这是一份数学五年级上册5 简易方程2 解简易方程等式的性质精品课件ppt,共14页。PPT课件主要包含了复习导入,探究新知,你发现了什么,等式的性质1,等式的性质2,根据等式的性质填空,15×5,填空题,x52,-4x20等内容,欢迎下载使用。
小学人教版等式的性质示范课课件ppt: 这是一份小学人教版等式的性质示范课课件ppt,共19页。PPT课件主要包含了天平平衡,a2b,①加1个茶杯,②加2个茶杯,③加1个茶壶,a+a2b+a,a+b4b,a+b-b4b-b,拿掉1个花瓶,你发现了什么等内容,欢迎下载使用。
小学数学人教版五年级上册等式的性质背景图ppt课件: 这是一份小学数学人教版五年级上册等式的性质背景图ppt课件,共17页。PPT课件主要包含了课堂目标,情景导入,新知探究,探索等式的性质1,a表示茶壶的质量,b表示单个茶杯的质量,天平平衡,a2b,加一个茶杯,a+b2b+b等内容,欢迎下载使用。














