





- 21.2.1配方法课件 课件 0 次下载
- 21.2.2公式法课件 课件 0 次下载
- 21.2.3因式分解法课件 课件 0 次下载
- 21.3实际问题与一元二次方程课件 课件 0 次下载
- 22.1.1二次函数的定义课件 课件 0 次下载
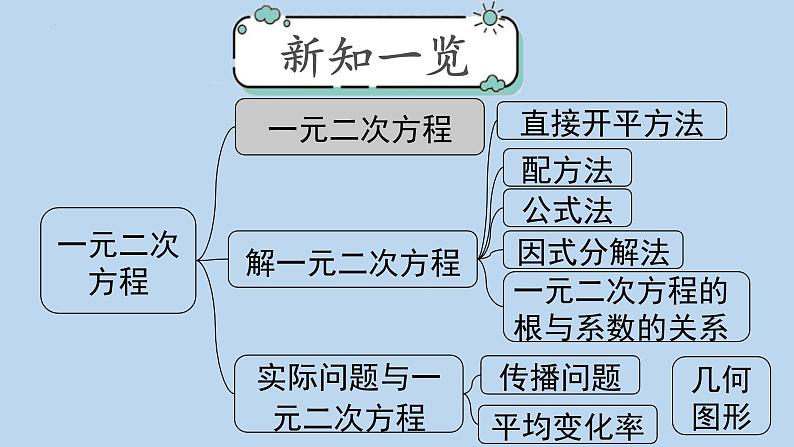
人教版九年级上册21.1 一元二次方程精品课件ppt
展开实际问题与一元二次方程
一元二次方程的根与系数的关系
知识点 1:一元二次方程的概念
对于上述问题请抽象出数学模型并列出合适的方程.
已知 AB = 2m,
解:设雕像下部 BC = x m,列方程得 x 2 = 2(2 - x ),整理得 x 2 + 2x - 4 = 0.①
方程 ① ② ③ 有什么共同点?
(1) 方程的两边都是_____;
(2) 都只含_____个未知数;
(3) 未知数的最高次数都是__.
x2 - 75x+350 = 0 ②
x2 + 2x - 4 = 0 ①
x2 - x = 56 ③
类比一元一次方程的特征填空.
要组织一次排球邀请赛,参赛的每两个队之间都要比赛一场,根据场地和时间等条件,赛程计划安排7天,每天安排4场比赛,比赛组织者应邀请多少个队参赛?
(2)最高次数是2;(3)方程两边都是整式.
像这样的等号两边都是整式,只含有一个未知数(一元),并且未知数的最高次数是2(二次)的方程,叫做一元二次方程.
x2-75x+350=0
2x2+3x-2=0
x2-x=56
请口答下面问题. (1)下面三个方程整理后含有几个未知数?
(3)方程两边都是整式吗?
(2)按照整式中的多项式的规定,它们最高次数是几次?
判断一个方程是一元二次方程需同时满足三个条件:
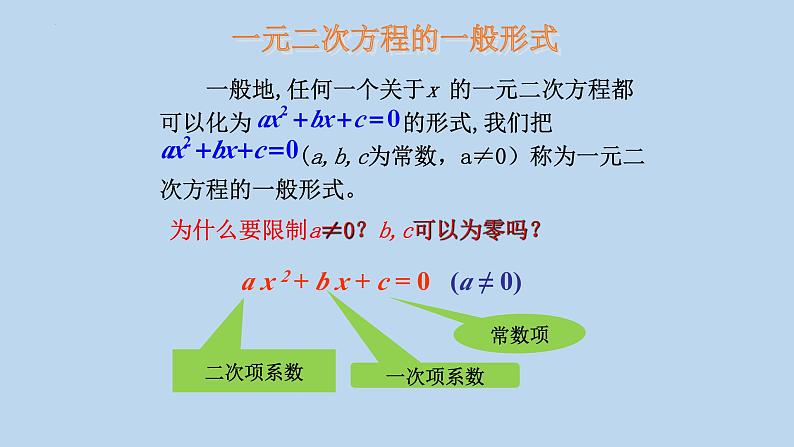
一元二次方程的一般形式
为什么要限制a≠0?b,c可以为零吗?
a x 2 + b x + c = 0
将方程3x(x-1)=5(x+2)化成一元二次方程的一般形式,并写出其中的二次项系数,一次项系数及常数项.
3x2-3x=5x+10.
移项,合并同类项,得一元二次方程的一般形式:
3x2-8x-10=0.
其中二次项系数为3,一次项系数为-8,常数项为-10.
请同学们自学课本一元二次方程的概念以下部分,勾画并记忆. 注意:1.理解并记住一元二次方程的一般形式、二次项、二次项系数等概念;2.思考问题“为什么规定a≠0?” ;
ax2 + bx + c = 0 (a≠0)
一元二次方程的一般形式:一般地,任何一个关于 x 的一元二次方程,经过整理,都能化成形式:ax2 + bx + c = 0 (a≠0)
1.一元二次方程的一般形式有什么特点?
若a=0,则二次项ax2的系数为0,二次项不存在。那么,方程就不是一元二次方程了。
2.“为什么规定a≠0?”
对比总结:一元一次方程与一元二次方程有什么区别与联系?
整式方程,只含有一个未知数
例题1:请你将方程3x(x-1)=5(x+2)化成一元二次方程的一般形式,并写出其中的二次项系数,一次项系数及常数项 。
解 :去括号,得移项,合并同类项,得一元二次方程的一般形式:其 中二次项系数为 ,一次项系数为 ,常数项为 .
3x2-3x=5x+10.
例题2:m为何值时,关于x的方程(m-1)xm2-1+2mx-3=0为一元二次方程。
解:由题意得:m2-1=2,m-1≠0,
整理,得 m2=3
2. 已知关于x的方程(k-2)x2-kx=x2-1. (1)当k取何值时,方程为一元二次方程? (2)当k取何值时,方程为一元一次方程?
画龙在于点睛 学习在于运用
同学们根据本节所学知识编写一道练习题,同桌交换解答,并在小组内交流。
通过本节课的学习谈谈你的收获和大家一起分享。
1、只含有一个未知数,并且未知数的最高次数是2的整式方程,叫做一元二次方程.
3、在实际问题转化为数学模型( 一元二次方程 ) 的过程中,体会学习一元二次方程的必要性和重要性.
人教版九年级上册第二十一章 一元二次方程21.1 一元二次方程备课ppt课件: 这是一份人教版九年级上册第二十一章 一元二次方程21.1 一元二次方程备课ppt课件,共14页。PPT课件主要包含了学习目标,化简得,知识归纳,一元二次方程的概念,当a0时,bx+c0,ax2+c0,ax20,3x+3y36,5x+10等内容,欢迎下载使用。
人教版九年级上册21.1 一元二次方程课文ppt课件: 这是一份人教版九年级上册21.1 一元二次方程课文ppt课件,共17页。PPT课件主要包含了情景思考,②只有一个未知数,③未知数最高次数是2,①等号两边都是整式,一元二次方程,课堂测试,小组讨论等内容,欢迎下载使用。
人教版九年级上册21.1 一元二次方程完美版ppt课件: 这是一份人教版九年级上册21.1 一元二次方程完美版ppt课件













