初中14.1.2 幂的乘方课前预习课件ppt

这是一份初中14.1.2 幂的乘方课前预习课件ppt，共26页。PPT课件主要包含了学习目标，新课导入，复习引入，n个a，am+n+p，am+n，am∙an，练一练，b10，y3n+6等内容，欢迎下载使用。

1.理解并掌握幂的乘方法则,会运用幂的乘方法则进行幂的 乘方的运算.（重点）2.掌握幂的乘方法则的推导过程.（难点）
即am∙an= （m，n都是正整数）.
幂的意义：a·a·…·a= .
同底数幂的乘法法则：同底数幂相乘，底数 ，指数 .
对于三个（或三个以上）的同底数幂相乘，有am∙an∙ap= （m，n，p都是正整数）.
同底数幂的乘法的逆应用：am+n= （m，n都是正整数）.
填空：(1) b5∙b5= ; (2) y2n∙yn+4∙y2 = ; (3) (m-n) 2∙(n-m) 4= ; (4) 已知a3=8，a5=32，则a8= .
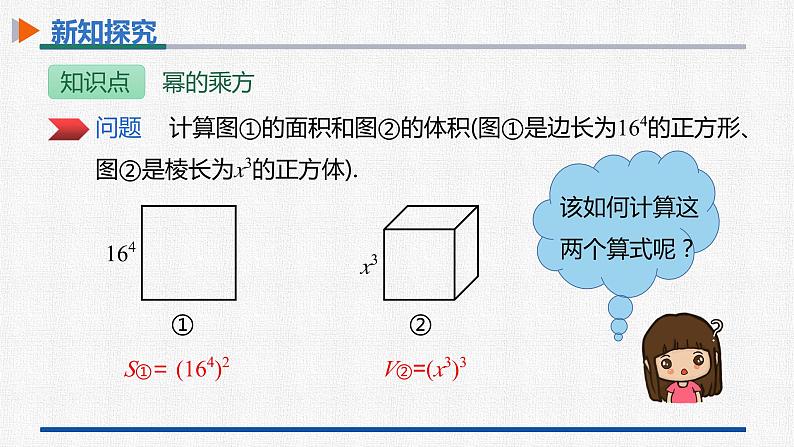
问题 计算图①的面积和图②的体积(图①是边长为164的正方形、图②是棱长为x3的正方体).
S①= (164)2
V②=(x3)3
(同底数幂的乘法法则)
根据乘方的意义及同底数幂的乘方，观察计算结果，你能发现什么规律？(1) (32)3=32×32×32=3（ ） ;(2) (a2)3=a2∙a2∙a2=a（ ） ;(3) (am)3=am∙am∙am=a（ ） （m是正整数）.
（1）(32)3=32×32×32=3（ ）
（2）(a2)3=a2∙a2∙a2=a（ ）
（3） (am)3=am∙am∙am=a（ ） （m是正整数）;
（3） (am)3=a3m（m是正整数）
（1）(32)3=36
（2）(a2)3=a6
观察：计算前后，（1）底数有何变化?
指数相乘得到结果中的指数
(am)n=amn （m，n都是正整数）
猜想：幂的乘方的运算法则，底数不改变，只需把指数相乘，字母表示为：
=am·am·…·am
=amn .
验证：一般地，对于任意底数a与任意正整数m，n，
使用该法则运算的前提条件有两个： ①乘方运算；②底数相同.
问题 [(am)n]p= （m，n，p都为正整数）.
=amn+mn+…+mn
=amnp .
=amn·amn·…·amn
如:[(y5)2]2= ;[(x5)m]n= .
（1）（103）5 ；
解: (1) (103)5 =103×5=1015；
(2) (a2)4 =a2×4=a8；
(3) (am)2 =am·2=a2m；
(4) -(x4)3 =-x4×3=-x12.
(3) -[(a-b)3 ]5 = -(a-b)3×5= -(a-b)15 .
例2 计算：(1)[ (an+1)2]3 ; (2) [(-x)7]4 ; (3) -[(a-b)3 ]5 .
解：(1)[ (an+1)2]3 = a(n+1)×2×3 = a6(n+1)= a6n+6 ;
(2) [(-x)7]4 = (-x)7×4 = (-x)28= x28 ;
(2)一定不要将幂的乘方与同底数幂的乘法混淆
同底数幂的乘法与幂的乘方的运算性质的区别
运用幂的乘方法则进行计算时，应注意：(1)底数不一定只是一个数或一个字母，也可以是单项式或多项式.
amn可以写成am的n次方的形式或an的m次方的形式
(am)n=amn （m，n都为正整数）
amn = (am)n= (an)m（m，n都为正整数）
填一填：x2m 可变形为（ ）m或（ ）2（1）若xm =3 ，则x2m 应变形为（ ）2，代入数值可知，x2m =（ ）2= ；
（2）若x2 =5 ，m=2，则x2m 应变形为（ ）m，代入数值可知，x2m =（ ）( )= .
幂的乘方，底数不变，指数相乘
(am)n=amn (m,n都是正整数）
[(am)n]p=amnp(m,n,p都是正整数）
amn =(am)n=(an)m (m,n都是正整数）
区分同底数幂的乘法法则与幂的乘方的法则
1.计算-（x3)5=（　　）A．x8 B．-x8C．x15D．-x15
2.下列各式的括号内，应填入b4的是( )A．b12＝(　　)8 B．b12＝(　　)6C．b12＝(　　)3 D．b12＝(　　)2
【解析】A、B均不是同类项，不能合并;C.根据同底数幂的乘法法则，a3•a2=a5;D.根据幂的乘方法则，（a3）2=a6．故选C．
3.（2021宁波模拟）下列各式的计算结果为a5的是( ) A.a3+a2 B.a6-a C.a3•a2 D.（a3）2
【解析】根据题意，得2m=（22）3，即2m=26，∴m=6.故选C．
(3)[(x-y)3]2+[(y-x)2]3.
(2)[(a2)3]5·[(-a)3]3;
(1)[x3·(-x)2]3；
解：(1)[x3·(-x)2]3=(x3·x2)3=(x5)3=x15；
(2)[(a2)3]5·[(-a)3]3=a2×3×5·(-a)3×3=a30·(-a)9=-a30·a9=-a39；
(3)[(x-y)3]2+[(y-x)2]3=(x-y)6+(y-x)6=(x-y)6+(x-y)6=2(x-y)6.
解：a4n-a6n = (a2n)2- (a2n)3 = 32-33 =-18 .
6.已知 a2n=3，求 a4n-a6n 的值.
7.(1)已知x2n＝3，求(x3n)4的值；
(2)已知2x＋5y－3＝0，求4x·32y的值．
解：(1) (x3n)4=x12n=
(2) ∵2x＋5y－3=0，∴2x＋5y=3,
=(22)x·(25)y=
22x·25y=22x＋5y=23=8.