



还剩27页未读,
继续阅读
所属成套资源:人教版数学八年级上册精品PPT课件整册打包
成套系列资料,整套一键下载
12.2第3课时三角形全等的判定(三) 课件 人教版数学八年级上册
展开
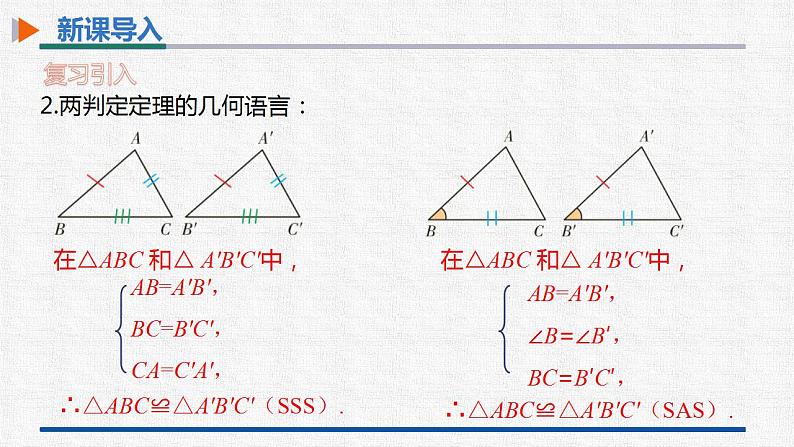
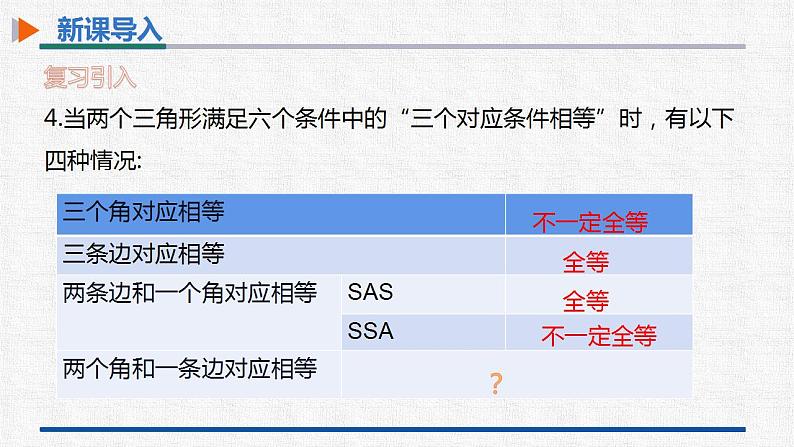
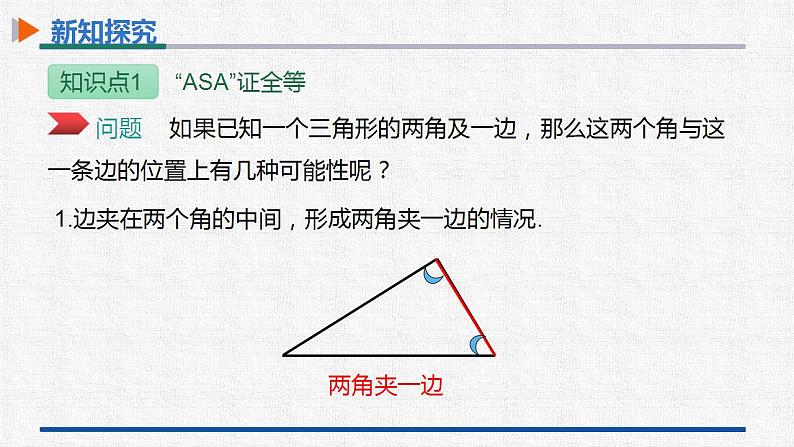
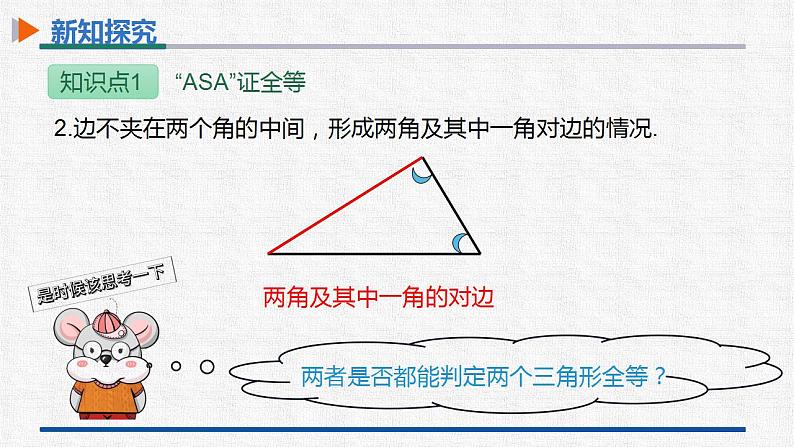
第十二章 全等三角形12.2 三角形全等的判定第3课时 三角形的全等的判定(三)(ASA,AAS) 学习目标-新课导入-新知探究-课堂小结-课堂训练 学习目标1.探索并正确理解三角形全等的判定方法“ASA”和“AAS”.(重点)2.能熟练利用三角形全等的判定方法“ASA”和“AAS”证明两个三角形全等.(难点) 新课导入复习引入 1.回顾我们已经学习过的判定三角形全等的两个定理. 边边边(SSS):三边分别相等的两个三角形全等.边角边(SAS):两边和它们的夹角分别相等的两个三角形全等. 新课导入复习引入2.两判定定理的几何语言:在△ABC 和△ A'B'C'中,∴△ABC≌△A'B'C'(SSS).在△ABC 和△ A'B'C'中,∴△ABC≌△A'B'C'(SAS). 新课导入复习引入 3.(1)我们已经总结过的找相等边的方法. ③等边加同边,其和还是等边. ①公共边. (2)我们已经总结过的找相等角的方法.①利用平行线可找到相等的角. ②正多边形的边相等.②对顶角.③等角加同角,其和还是等角.④等角减同角,其差还是等角.⑤等角的补角相等.⑥正多边形的内角相等. ④等边减同边,其差还是等边. 新课导入复习引入4.当两个三角形满足六个条件中的“三个对应条件相等”时,有以下四种情况:全等不一定全等不一定全等全等? 新知探究两角夹一边1.边夹在两个角的中间,形成两角夹一边的情况. 新知探究两角及其中一角的对边两者是否都能判定两个三角形全等?2.边不夹在两个角的中间,形成两角及其中一角对边的情况. 新知探究动手试一试 新知探究作法:(1)画A'B'=AB; (2)在A'B'的同旁画∠DA'B'=∠A,∠EB'A '=∠B,A'D, B'E相交于点C'.A′B′C′ED 新知探究思考 ① △A′B′C′ 与△ABC全等吗?②这两个三角形全等满足的是哪三个条件?全等两角一夹边A′B′C′ED 新知探究 新知探究在△ABC 和△ A'B'C'中,∴△ABC≌△A'B'C'(ASA).该判定定理的几何语言:注意:必须是两角的夹边就也是说,三角形的两个角的大小和它们的夹边的大小确定了,这个三角形的形状、大小就确定了. 新知探究例 在△ABC和△DEF中,∠A=∠D,∠B=∠E,BC=EF.求证:△ABC≌△DEF.证明:在△ABC中,∠A+∠B+∠C=180°.∴∠C=180°-∠A-∠B.同理 ∠F=180°-∠D-∠E.【分析】如果能证明∠C=∠F,就可以利用“角边角”证明△ABC和△DEF全等,由三角形内角和定理可以证明∠C=∠F. 新知探究例 在△ABC和△DEF中,∠A=∠D,∠B=∠E,BC=EF.求证:△ABC≌△DEF.∠B=∠E, BC=EF, ∠C=∠F,∴△ABC≌△DEF(ASA).又∠A=∠D,∠B=∠E,∴∠C=∠F.在△ABC和△DEF中, 新知探究问题 已知在△ABC中,∠B=60°,∠C=45°,AB=3cm,你能画出△A′B′C′,使△A′B′C′≌△ABC吗? 新知探究因为∠B=60°,∠C=45°,所以∠A=75°,则“AAS”可转化为“ASA”,那么△A′B′C′≌△ABC.75° 新知探究在△ABC 和△ A'B'C'中,∴△ABC≌△A'B'C'(AAS).该判定定理的几何语言:就也是说,三角形的两个角的大小和其中一个角的对边的长度确定了,这个三角形的形状、大小就确定了. 新知探究跟踪训练 新知探究如图,已知∠ACB=∠DBC,∠ABC=∠CDB,判别下面的两个三角形是否全等,并说明理由. 解:不全等,因为BC虽然是公共边,但不是对应边. 新知探究思考 三角分别相等的两个三角形全等吗?不一定全等假设三个角分别为30°,60°和90°. 新知探究判定两个三角形全等的方法SSS,SAS,ASA,AAS 课堂小结三角形的全等的判定(三)(ASA,AAS)内容两角和它们的夹边对应相等的两个三角形全等已知两角,必须找“夹边” 注意事项有两角和一边分别相等的两个三角形不一定全等.内容注意事项两角分别相等且其中一组等角的对边相等的两个三角形全等.SSS,SAS,ASA,AAS 课堂训练1.如图,小明不慎将一块三角形模具打碎为三块,他想配一块与原来一样的三角形模具,为了方便,应该带哪块去商店?( )A.1 B.2 C.3 D.三块都带去 A 课堂训练2.(2021•重庆)如图,在△ABC和△DCB中,∠ACB=∠DBC,添加一个条件,不能证明△ABC和△DCB全等的是( )A.∠ABC=∠DCB B.AB=DC C.AC=DB D.∠A=∠DB【解析】已知∠ACB=∠DBC,BC=BC,A:当∠ABC=∠DCB时,可用ASA证明;B:当AB=DC时,不能证明两三角形全等;C:当AC=DB时,可用SAS证明;D:当∠A=∠D时,可用AAS证明.故选B. 课堂训练3.(2021•齐齐哈尔)如图,AC=AD,∠1=∠2,要使△ABC≌△AED,应添加的条件是 .(只需写出一个条件即可)【解析】∵∠1=∠2,∴∠1+∠BAD=∠2+∠BAD,即∠BAC=∠EAD.∵AC=AD,∴当添加∠B=∠E时,可根据“AAS”判断;当添加∠C=∠D时,可根据“ASA”判断;当添加AB=AE时,可根据“SAS”判断.(任选其中一个条件即可). 课堂训练4.(2021•衡阳)如图,点A、B、D、E在同一条直线上,AB=DE,AC∥DF,BC∥EF.求证:△ABC≌△DEF. 课堂训练5.(2021•泸州)如图,点D在AB上,点E在AC上,AB=AC,∠B=∠C,求证:BD=CE. 课堂训练6.(2021•铜仁市)如图,AB交CD于点O,在△AOC与△BOD中,有下列三个条件:①OC=OD,②AC=BD,③∠A=∠B.请你在上述三个条件中选择两个为条件,另一个能作为这两个条件推出来的结论,并证明你的结论(只要求写出一种正确的选法).(1)你选的条件为 、 , 结论为 ;(2)证明你的结论. 课堂训练①OC=OD,②AC=BD,③∠A=∠B. 课堂训练解:选的条件为②、③ ,结论为①. 证明:在△AOC和△BOD中, ∠AOC=∠BOD, ∠A=∠B, AC=BD,∴△AOC≌△BOD(AAS),∴OC=OD.①OC=OD,②AC=BD,③∠A=∠B. 课堂训练①OC=OD,②AC=BD,③∠A=∠B.若选的条件为①、② ,得不到结论③,因为“SSA”不能作为判定全等的定理.再结合∠AOC=∠BOD, 课堂训练7.(2021•陕西模拟)如图,在△DAE和△ABC中,D是AC上一点,AD=AB,DE∥AB,∠E=∠C.求证:AE=BC. 课堂训练8.如图,点E、C、D、A在同一条直线上,AB∥DF,ED=AB,∠E=∠CPD.求证:BC=EF. 课堂训练9.(2021•西安一模)如图,在△ABC中,∠ABC=90°,BD⊥AC于点D,点E在DB的延长线上,DE=BC,∠1=∠2,求证:DF=AB.
相关资料
更多









