数学必修 第二册7.3* 复数的三角表示教案设计

第七章 复数

7.3* 复数的三角表示

7.3.2 复数乘、除运算的三角表示及几何意义

教学设计

一、教学目标

1.   通过复数的几何意义，了解复数的三角表示。
2.   了解复数乘、除运算的三角表示及几何意义。

二、教学重难点

1.   教学重点

复数乘、除运算的三角表示及几何意义。

2.   教学难点

复数乘、除运算的三角表示及几何意义。

三、教学过程

1. 新课导入

前面，我们研究了复数代数形式的乘、除运算，下面我们利用复数的三角表示研究复数的乘、除运算及其几何意义。

2. 探索新知

如果把复数z1，z2分别写成三角形式z1=r1(cos1+isin1)，z2= r2(cos2+isin2)，你能计算z1z2并将结果表示成三角形式吗？

根据复数的乘法法则以及两角和的正弦、余弦公式，可以得到

z1z2=r1(cos1+isin1) r2(cos2+isin2)

= r1r2(cos1+isin1) (cos2+isin2)

= r1r2[(cos1cos2-sin1sin2)+i(sin1cos2+cos1sin2)]

= r1r2[cos(1+2)+isin(1+2)]

即r1(cos1+isin1) r2(cos2+isin2)= r1r2[cos(1+2)+isin(1+2)]

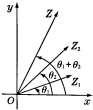这就是说，两个复数相乘，积的模等于各复数的模的积，积的辐角等于各复数的辐角的和。

两个复数z1，z2相乘时，可以像左图那样，先分别画出与z1，z2对应的向量，，然后把向量绕点O按逆时针方向旋转角2（如果2<0，就要把绕点O按顺时针方向旋转角|2|），再把它的模变为原来的r2倍，得到向量，表示的复数就是积z1z2。这就是复数乘法的几何意义。

设z1=r1(cos1+isin1)，z2= r2(cos2+isin2)，且z1z2，因为r2(cos2+isin2)[cos(1-2)+isin(1-2)]= r1(cos1+isin1)，所以根据复数除法的定义，有[cos(1-2)+isin(1-2)]。

这就是说，两个复数相除，商的模等于被除数的模除以除数的模所得的商，商的辐角等于被除数的辐角减去除数的辐角所得的差。

3. 课堂练习

见课本P89练习及习题。

4. 小结作业

小结：本节课学习了复数乘、除运算的三角表示及几何意义。

作业：完成本节课课后习题。

四、板书设计

7.3.2复数乘、除运算的三角表示及几何意义

复数乘法运算的三角表示：r1(cos1+isin1) r2(cos2+isin2)= r1r2[cos(1+2)+isin(1+2)]

复数除法运算的三角表示：[cos(1-2)+isin(1-2)]