第1章 有理数 知识梳理-浙教版七年级数学上册章节复习

有理数知识梳理

一、正数与负数

1.如+3、+1.5、、+584等大于0的数，叫做正数；如－3、－1.5、、－584等小于0的数，叫做负数．

【注】①一个数前面的“+”“-”是这个数的性质符号， “+”常省略，但 “-”不能省略.

②带“+”号的数不一定是正数，带“-”的数不一定是负数，如a＜0时，+a表示一个负数，而-a表示一个正数．

③0既不是正数也不是负数，它是正数和负数的分界线．

2.相反意义的量

（1）定义：我们把一种意义的量规定为正的，把另一种和它意义相反的量规定为负的，就产生了正数和负数.

（2）具有相反意义的量的特点：

①具有相反意义的量是成对出现的，单独一个量不能成为具有相反意义的量；

②与一个量意义相反的量不止一个；

③具有相反意义的量包含两个要素：一是它们的意义相反，二是它们都具有数量；

④具有相反意义的量必须是同类量，如节约1吨水和浪费3吨油不是具有相反意义的量.

二、有理数的分类

1.定义：整数和分数统称为有理数.

2.分类

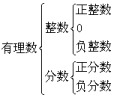（1）按整数、分数的关系分类：   （2）按正数、负数与0的关系分类：　
　　　                 　　

【注】①有理数都可以写成分数的形式，整数也可以看作是分母为1的数.

②分数与有限小数、无限循环小数可以互化，所以有限小数和无限循环小数可看作分数，但无限不循环小数不是分数，例如．

③正数和零统称为非负数；负数和零统称为非正数；正整数、0、负整数统称整数．

④在对有理数进行分类时，要做到不重不漏.

三、数轴

1.定义：规定了原点、正方向和单位长度的直线叫做数轴.

【注】①原点、正方向和单位长度是数轴的三要素，三者缺一不可；

      ②数轴是一条可以向两端无限延长的直线；

      ③原点的位置、单位长度、正方向都是根据实际需要规定的；

      ④一般地，数轴上原点右边的点表示正数，左边的点表示负数；反过来也对，即正数用数轴上原点右边的点表示，负数用原点左边的点表示，零用原点表示.

2. 数轴与有理数的关系：任何一个有理数都可以用数轴上的点来表示，但数轴上的点不都表示有理教，还可以表示其他数，比如.

四、相反数

1.定义：只有符号不同的两个数互为相反数；0的相反数是0.

2.性质：

（1）互为相反数的两数的点分别位于原点的两旁，且与原点的距离相等（这两个点关于原点对称）.

（2）数a的相反数是-a，互为相反数的两数和为0.

五、绝对值

1.定义：一般地，数轴上表示数a的点与原点的距离叫做数a的绝对值，记作|a|.

2.绝对值的代数意义：一个正数的绝对值是它本身；一个负数的绝对值是它的相反数；0的绝对值是0．即对于任何有理数a都有：

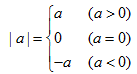
3.绝对值的几何意义：一个数的绝对值就是表示这个数的点到原点的距离，离原点的距离越远，绝对值越大；离原点的距离越近，绝对值越小．

4．性质：

（1）0除外，绝对值为一正数的数有两个，它们互为相反数．

（2）互为相反数的两个数的绝对值相等.

（3）绝对值具有非负性，即任何一个数的绝对值总是正数或0．

六、有理数的大小比较

1．数轴比较法：在数轴上表示出两个有理数，左边的数总比右边的数小．

2.代数比较法：两个数比较大小，按数的性质符号分类，情况如下：

3.作差比较法：设a、b为任意数，若a-b＞0，则a＞b；若a-b＝0，则a＝b；若a-b＜0，a＜b；反之成立．

4.求商比较法：设a、b为任意正数，若，则；若，则；若，则；反之也成立．若a、b为任意负数，则与上述结论相反．

5.倒数比较法：如果两个数都大于零，那么倒数大的反而小．