人教版九年级上册22.2二次函数与一元二次方程精品导学案

这是一份人教版九年级上册22.2二次函数与一元二次方程精品导学案，共4页。学案主要包含了学习目标，重点难点，新知准备，课堂探究，学后反思等内容，欢迎下载使用。

【学习目标】
1.经历探索二次函数与一元二次方程关系的过程，体会方程与函数之间的联系；
2.理解抛物线与轴公共点的个数与相应的一元二次方程根的对应关系；
3.会求抛物线与坐标轴的交点坐标.
【重点难点】
重点：一次函数图象与一元二次方程的关系，抛物线与轴三类交点情况．
难点：抛物线与轴公共点的个数与相应的一元二次方程根的对应关系.
【新知准备】
1.口述二次函数的图象和性质.
2. 解下列方程:
① ② ③
3.对于任何一个一元二次方程，我们可以通过表达式 的值判断方程的根的情况如下：当 时，方程有 实数根；
当 时，方程有 实数根；
当 时，方程 实数根
【课堂探究】
一、自主探究
探究1
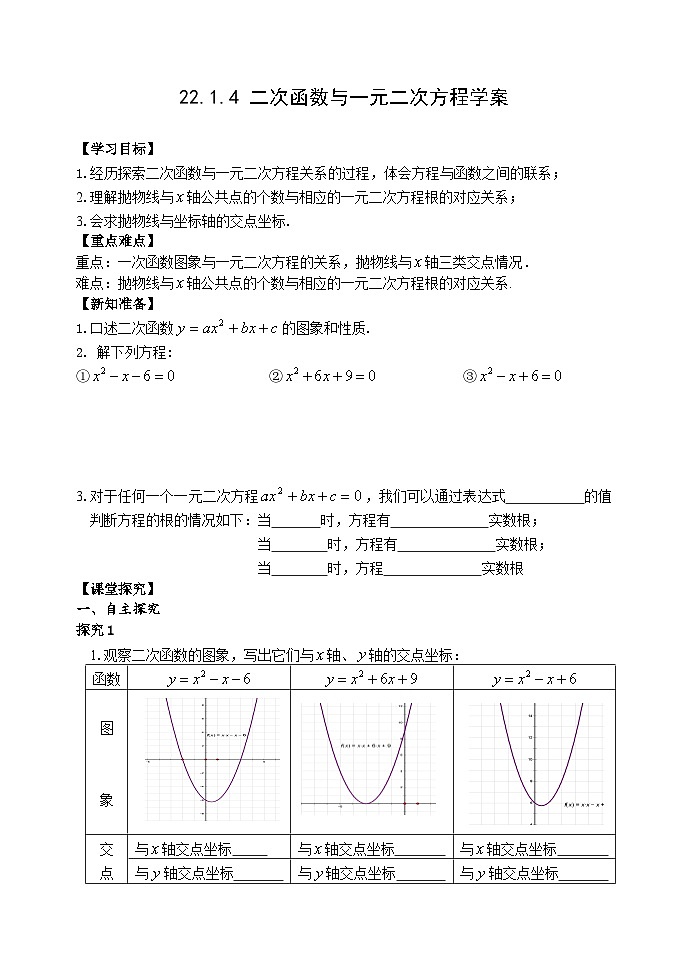
1.观察二次函数的图象，写出它们与轴、轴的交点坐标：
2.对比《新知准备》第2题各方程的解，你发现什么？

3.归纳总结：
⑴一元二次方程的实数根就是对应的二次函数与
轴交点的 .
⑵二次函数与一元二次方程的关系如下：（一元二次方程的实数根记为）
⑶二次函数与轴交点坐标是 .
探究2
已知二次函数.求该抛物线的图象与坐标轴的交点坐标.
方法归纳：
⑴求抛物线与轴的交点坐标只要令 ，转化为求对应方程 的解；若对应方程的实数根为，则抛物线与轴的交点坐标是 ，特别当时，这个交点就是抛物线的 .
⑵求抛物线与轴的交点坐标只要令 ，该交点坐标是 .这也是求任意函数的图象与坐标轴交点坐标的一般方法.
二、尝试应用
1.抛物线与轴的两个交点坐标为(4,0)和,则关于的一元二次方程的两根为 .
2.二次函数与轴有 个的交点,坐标是 ,这两点间的离是 .
3. 抛物线与轴有两个交点,则m的取值范围是 ．
三、补偿提高
1.二次函数的值永远为负数的条
件是( )．
A． B．
C． D．
2. 二次函数图象如图所示，
则不等式的解集是 ．
不等式的解集是
【学后反思】
1.通过本节课的学习你有那些收获?
2. 你还有哪些疑惑？
2.2 二次函数与一元二次方程学案答案

【新知准备】
1.略.
2. (1) ， (2) (3)无实数根.
3.=, ＞0,两个不相等的, =0两个相等的,＜0,无实数根.
【课堂探究】
二、尝试应用
1. ，
2. 两, (1,0) (2,0),1个单位.
3. ,
三、补偿提高
1.D
2.(1) x＜-2或x＞6.(2)-2＜x＜6.
函数
图
象
交
点
与轴交点坐标
与轴交点坐标
与轴交点坐标
与轴交点坐标
与轴交点坐标
与轴交点坐标
二次函数
与
一元二次方程
图象
与轴交点
判别式

有 个交点,
坐标为
0，方程
实数根,是 .
有 个交点,
坐标为
0，方程
实数根,是 .
有 个交点,
坐标为
0，方程
实数根.