









2021学年19.2.3一次函数与方程、不等式练习题课件ppt
展开1.理解一次函数与二元一次方程(组)的关系,会用一次函数图象解二元一次方程组;2.能综合应用一次函数及二元一次方程(组)知识解决相关实际问题.3.让学生了解到函数是刻画和研究现实世界数量关系的重要数学模型,也是一种重要的数学思想,培养和提高学生在数学学习中的创造和应用函数的能力。
我们来看下面两个问题有什么关系? 1.解不等式5x+6>3x+10. 2.当自变量x为何值时函数y=2x-4的值大于0?
在问题1中,不等式5x+6>3x+10可以转化为2x-4>0,解这个不等式得x>2.
解问题2就是要解不等式2x-4>0,得出x>2时函数y=2x-4的值大于0.
因此这两个问题实际上是同一个问题.
那么,是不是所有的一元一次不等式都可以转化为一次函数的相关问题呢?它在函数图象上的表现是什么?如何通过函数图象来求解一元一次不等式?
观察函数y=2x-4的图象,可以看出:当x>2时,直线y=2x-4上的点全在x轴上方,即这时y=2x-4>0。
由于任何一元一次不等式都可以转化为ax+b>0或ax+b<0(a,b为常数,a≠0)的形式,所以解一元一次不等式可以看作:当一次函数的函数值大于(或小于)0时,求相应自变量的取值范围.
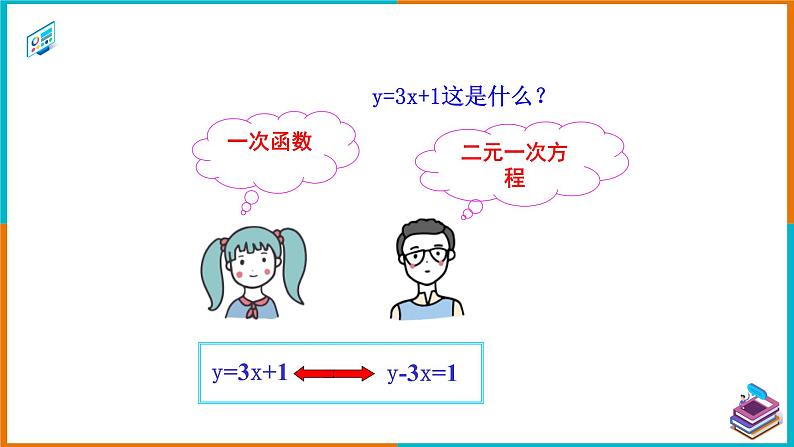
y=3x+1这是什么?
从函数的角度看二元一次方程组
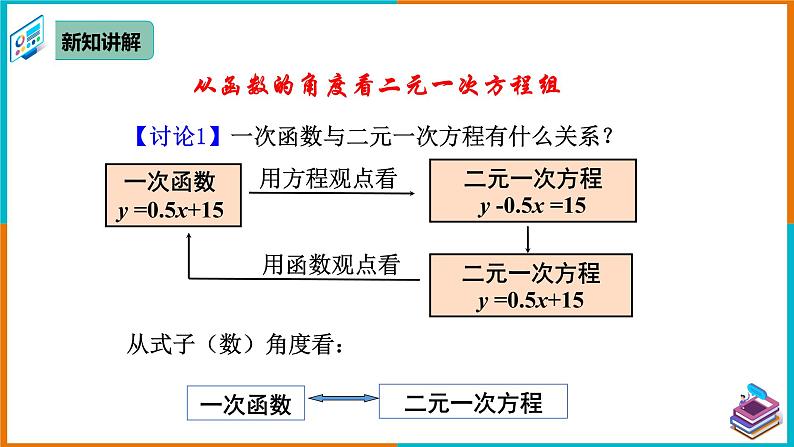
【讨论1】一次函数与二元一次方程有什么关系?
由函数图象的定义可知:直线y =0.5x+15上的每个点的坐标(x,y)都能使等式y=0.5x+15成立,即直线y =0.5x+15上的每个点的坐标都是二元一次方程y=0.5x+15的解.
【讨论2】从形的角度看,一次函数与二元一次方程有什么关系?
二元一次方程组的解就是相应的 两个一次函数图象 的交点坐标.
从形的角度看,二元一次方程组与一次函数有什么关系?
一般地,因为每个含有未知数x和y的二元一次方程的等式,都可以改写为( )的形式,所以每个这样的方程都对应一个一次函数,于是也对应 .这条直线上每个点的坐标(x ,y)都是这个二元一次方程的解.
从“数”的角度看:解二元一次方程组,相当于求自变量为何值时相应的两个函数值相等,以及这个函数值是多少; 从“形”的角度看:解二元一次方程组,相当于确定两条直线的交点坐标.因此,我们可以用画一次函数图象的方法得到方程组的解.
例、考虑下面两种移动电话计费方式:
用函数方法解答何时两种计费方式费用相等.
解:设通话时间为x分,若按“方式一”计费方式,则收取费用y=30+0.3x;若按“方式二”计费方式收取费用,则收取费用y=0.4x.在同一直角坐标系中分别画出这两个函数的图象,如下图:
所以两图象交于点(300,120),
当x=300时,30+0.3x=0.4x,
即当一个月内通话时间等于300分钟时,选择两种计费方式费用相等.
二元一次方程组的解与以这两个方程所对应的一次函数图象的交点坐标相对应。
由此可得: 二元一次方程组的图象解法:
写函数,作图象,找交点,下结论
方程组的解 对应两条直线交点的坐标.
1、以方程2x-y=1的解为坐标的点都在一次函数 _________的图像上。2、方程组 的解是_______ ,由此可知一次函数 ___ 与 ___ 的图像必有一个交点,且交点坐标是______ 。
3、方程组 的解是 则函数 与 的交点P的坐标是______ 4、一次函数y=3x-4的图象是一条直线,它由无数个点组成的,那么方程3x-y=4 的解有( )A.1个 B.2个 C.3个 D.无数个
5、小亮用作图象的方法解二元一次方程组时,在同一直角坐标系内作出了相应的两个一次函数的图象 l1、l2如图 ,他解的这个方程组是( )
点拨:由图象知l1、l2 的 x 的系数都应为负数,排除 A、C.又 l1、l2的交点为(2,-2),代入验证可知只有 D 符合.
6、一次函数y1=4x+5与y2=3x+10的图象如图所示,则4x+5>3x+10的解集是( ) A.x<5 B.x>5 C.x>-5 D.x>25
7、某长途汽车客运站规定,乘客可以免费携带一定质量的行李,但超过该质量则需购买行李票,且行李费y(元)是行李质量x(kg)的一次函数.现知李明带了60 kg的行李,交了行李费5元;张华带了90 kg的行李,交了行李费10元.(1)写出y与x之间的函数表达式;(2)旅客最多可免费携带多少kg的行李?
解:(1)设此一次函数表达式为:y=kx+b(k≠0) . 根据题意,可得方程组
(2)当x=30时,y=0.
所以旅客最多可免费携带30 kg的行李.
解二元一次方程组:从“数”的角度看相当于求自变量为何值时相应的两个函数值相等,以及这个函数值是多少; 从“形”的角度看相当于确定两条直线的交点坐标.
人教版八年级下册19.2.2 一次函数一等奖习题课件ppt: 这是一份人教版八年级下册19.2.2 一次函数一等奖习题课件ppt,文件包含1923《一次函数与方程不等式》课件pptx、192《习题》课件pptx、1923《一次函数与方程不等式》导学案doc、1923《一次函数与方程不等式》教案doc等4份课件配套教学资源,其中PPT共66页, 欢迎下载使用。
人教版八年级下册19.2.2 一次函数一等奖课件ppt: 这是一份人教版八年级下册19.2.2 一次函数一等奖课件ppt,文件包含1923一次函数与方程不等式pptx、1923一次函数与方程不等式导学案doc、1923一次函数与方程不等式教案doc等3份课件配套教学资源,其中PPT共42页, 欢迎下载使用。
初中数学人教版八年级下册第十九章 一次函数19.2 一次函数19.2.2 一次函数精品ppt课件: 这是一份初中数学人教版八年级下册第十九章 一次函数19.2 一次函数19.2.2 一次函数精品ppt课件,文件包含1923一次函数与方程不等式pptx、RJ中学数学八年级下第十九章1923一次函数与方程不等式第1课时教学详案docx、RJ中学数学八年级下第十九章1923一次函数与方程不等式第2课时教学详案docx等3份课件配套教学资源,其中PPT共27页, 欢迎下载使用。













