高中数学2.1 等差数列的概念及其通项公式一等奖ppt课件

这是一份高中数学2.1 等差数列的概念及其通项公式一等奖ppt课件，共33页。PPT课件主要包含了递增数列，递减数列，常数列，答案B，答案C，答案D等内容，欢迎下载使用。

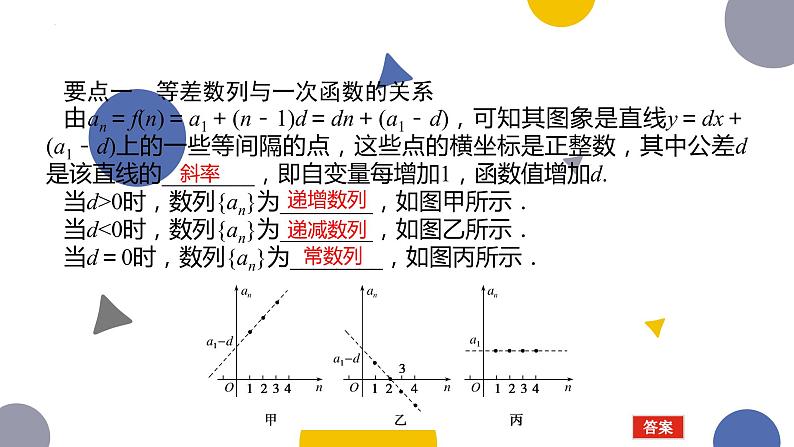
要点一　等差数列与一次函数的关系由an＝f(n)＝a1＋(n－1)d＝dn＋(a1－d)，可知其图象是直线y＝dx＋(a1－d)上的一些等间隔的点，这些点的横坐标是正整数，其中公差d是该直线的________，即自变量每增加1，函数值增加d.当d>0时，数列{an}为________，如图甲所示．当d<0时，数列{an}为________，如图乙所示．当d＝0时，数列{an}为________，如图丙所示．
1．判断正误(正确的画“√”，错误的画“×”)(1)数列{an}的通项公式为an＝3n＋5，则数列{an}的公差与函数y＝3x＋5的图象的斜率相等．(　　)(2)等差数列{an}的单调性与公差d有关．(　　)(3)若三个数a，b，c满足2b＝a＋c，则a，b，c一定是等差数列．(　　)(4)任意两个实数都有等差中项．(　　)
2．已知点(1，5)，(2，3)是等差数列{an}图象上的两点，则数列{an}为(　　)A．递增数列　 B．递减数列C．常数列 D．无法确定
3．若5，x，y，z，21成等差数列，则x＋y＋z的值是(　　)A．26 B．29C．39 D．52
解析：因为5，x，y，z，21成等差数列，所以y既是5和21的等差中项也是x和z的等差中项，所以5＋21＝2y，∴y＝13，∴x＋z＝2y＝26∴x＋y＋z＝39.故选C.
4．在△ABC中，三个内角A、B、C成等差数列，则B等于________.
解析：因为三个内角A、B、C成等差数列，所以2B＝A＋C，又因为A＋B＋C＝180°，所以3B＝180°，所以B＝60°.
题型一　等差数列与一次函数的关系例1　已知(2，1)，(4，5)是等差数列{an}图象上的两点．(1)求这个数列的通项公式；(2)判断(n，17)是否是{an}图象上的点，若是，求出n的值，若不是，说明理由；(3)判断这个数列的增减性，并求其最小正数项．
(1)根据等差数列图象上的两点求通项公式的一般方法是设出an＝dn＋b，将图象上的点代入，求d，b.(2)判断等差数列增减性的方法主要有两种，一是公差法：d>0递增；d<0递减；d＝0不单调．二是图象法：图象上升递增；下降递减；图象不上升也不下降，不单调．
跟踪训练1　在数列{an}中，a1＝3，a10＝21，已知该数列的通项公式是关于n的一次函数，则a2 021＝________．
题型二　等差中项例2　已知三个数成等差数列，其和为15，其平方和为83，则这三个数分别为________．
答案：3，5，7或7，5，3
变式探究　已知四个数成等差数列，它们的和为26，中间两项的积为40，求这四个数．
当等差数列{an}的项数n为奇数时，可设中间的一项为a，再以d为公差向两边分别设项，即设为…，a－2d，a－d，a，a＋d，a＋2d，…；当等差数列的项数n为偶数时，可设中间两项分别为a－d，a＋d，再以2d为公差向两边分别设项，即设为…，a－3d，a－d，a＋d，a＋3d，….
题型三　等差数列性质的应用例3　(1)在等差数列{an}中，已知a2＋a5＋a8＝9，a3a5a7＝－21，则an＝________________．(2)在等差数列{an}中，a4＋a7＋a10＝17，a4＋a5＋a6＋…＋a12＋a13＋a14＝77，且ak＝13，则k＝________．
2n－7或－2n＋13
跟踪训练3　(1)在等差数列{an}中，若a3＋a5＋a7＋a9＋a11＝100，则3a9－a13的值为(　　)A．20 B．30C．40 D．50(2)设数列{an}，{bn}都是等差数列，且a1＋b1＝7，a3＋b3＝21，则a5＋b5＝________．
答案：(1)C　(2)35
解析：(1)∵a3＋a11＝a5＋a9＝2a7，∴a3＋a5＋a7＋a9＋a11＝5a7＝100，∴a7＝20.∴3a9－a13＝3(a7＋2d)－(a7＋6d)＝2a7＝40.故选C.(2)因为{an}，{bn}都是等差数列所以{an＋bn}是等差数列设{an＋bn}的公差为d则(a3＋b3)－(a1＋b1)＝2d∴d＝7∴a5＋b5＝(a3＋b3)＋2d＝21＋2×7＝35.
题型四　等差数列的实际应用例4　某公司经销一种数码产品，第1年可获利200万元．从第2年起，由于市场竞争等方面的原因，其利润每年比上一年减少20万元，按照这一规律，如果公司不开发新产品，也不调整经营策略，从哪一年起，该公司经销这一产品将亏损？
解析：设从第1年起，第n年的利润为an，则由题意知a1＝200，an－an－1＝－20(n≥2，n∈N＋)．所以每年的利润an可构成一个等差数列{an}，且公差d＝－20.从而an＝a1＋(n－1)d＝220－20n.若an<0，则该公司经销这一产品将亏损，由an＝220－20n<0，得n>11，即从第12年起，该公司经销此产品将亏损．
解决实际应用问题，首先要认真领会题意，根据题目条件，寻找有用的信息．若一组数按次序“定量”增加或减少时，则这组数成等差数列．合理地构建等差数列模型是解决这类问题的关键，在解题过程中，一定要分清首项、项数等关键的问题．
跟踪训练4　某市出租车的计价标准为1.2元/km，起步价为10元，即最初的4 km(不含4 km)计费10元．如果某人乘坐该市的出租车去往14 km处的目的地，且一路畅通，等候时间为0，求需要支付的车费．
解析：根据题意，当该市出租车的行程大于或等于4 km时，每增加1 km，乘客需要支付1.2元．所以可以建立一个等差数列{an}来计算车费．令a1＝11.2，表示4 km处的车费，公差d＝1.2，那么当出租车行至14 km处时，n＝11，此时需要支付车费a11＝11.2＋(11－1)×1.2＝23.2(元)．
易错辨析　混淆等差数列的公共项问题中n的取值致错例5　两个等差数列5，8，11，…和3，7，11，…都有100项，那么它们共有多少相同的项？
1．已知数列{an}的通项公式是关于n的一次函数，a3＝7，a7＝19，则a10的值为(　　)A．26 B．28C．30 D．32
2．已知m和2n的等差中项是4，2m和n的等差中项是5，则m和n的等差中项是(　　)A．8 B．6C．4.5 D．3
4．在等差数列{an}中，已知a4＋a8＝16，则a2＋a10＝________.
解析：由等差数列的性质知，a2＋a10＝a4＋a8＝16.
5．一个等差数列由三个数组成，三个数的和为9，三个数的平方和为35，求这个数列．