初中数学人教版七年级下册5.3.1 平行线的性质教学课件ppt

这是一份初中数学人教版七年级下册5.3.1 平行线的性质教学课件ppt，文件包含《531平行线的》精品课件pptx、《531平行线的性质》精品教学方案doc、《531平行线的性质》同步练习docx等3份课件配套教学资源，其中PPT共22页， 欢迎下载使用。

经历探索和操作，了解平行线的特征，进一步提高推理能力；理解和掌握平行线的性质：会用平行线的性质进行简单的计算和证明．
重点：平行线性质的探索及对性质的理解.难点：能用平行线的性质解决相关问题,并有条理地表达和推理.
根据右图，填空：①如果∠1＝∠C，　那么＿＿∥＿＿（　　　　　 　 ）② 如果∠1＝∠B 那么＿＿∥＿＿（　　 　　 　 ）③ 如果∠2＋∠B＝180°，　那么＿＿∥＿＿（ 　　 ）
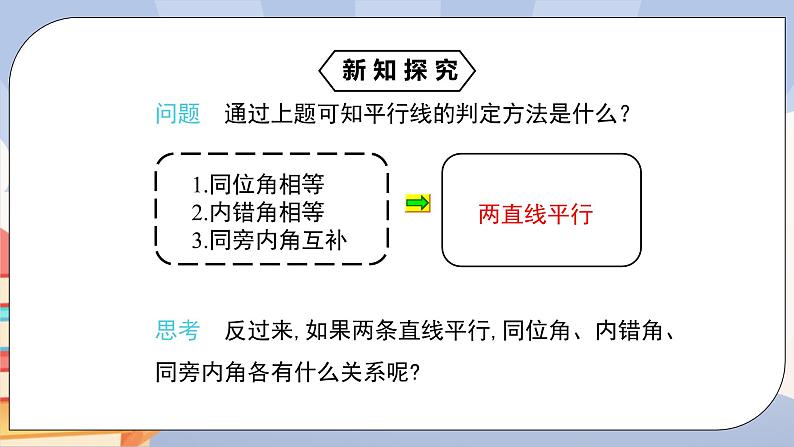
同位角相等，两直线平行
内错角相等，两直线平 行
同旁内角互补,两直线平行
问题 通过上题可知平行线的判定方法是什么？
思考 反过来,如果两条直线平行,同位角、内错角、同旁内角各有什么关系呢?
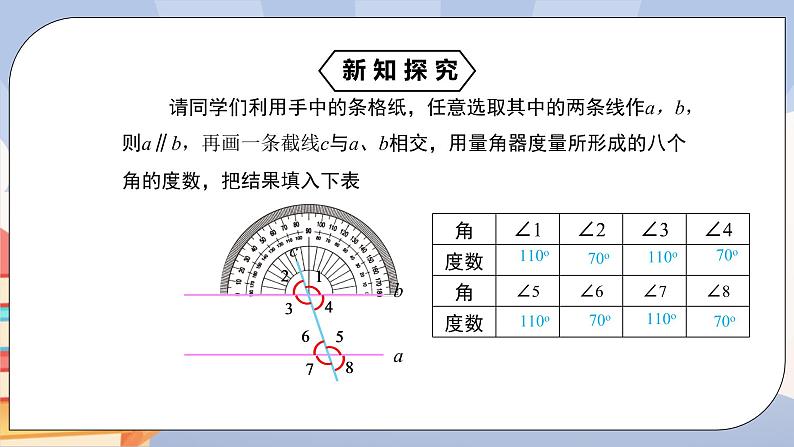
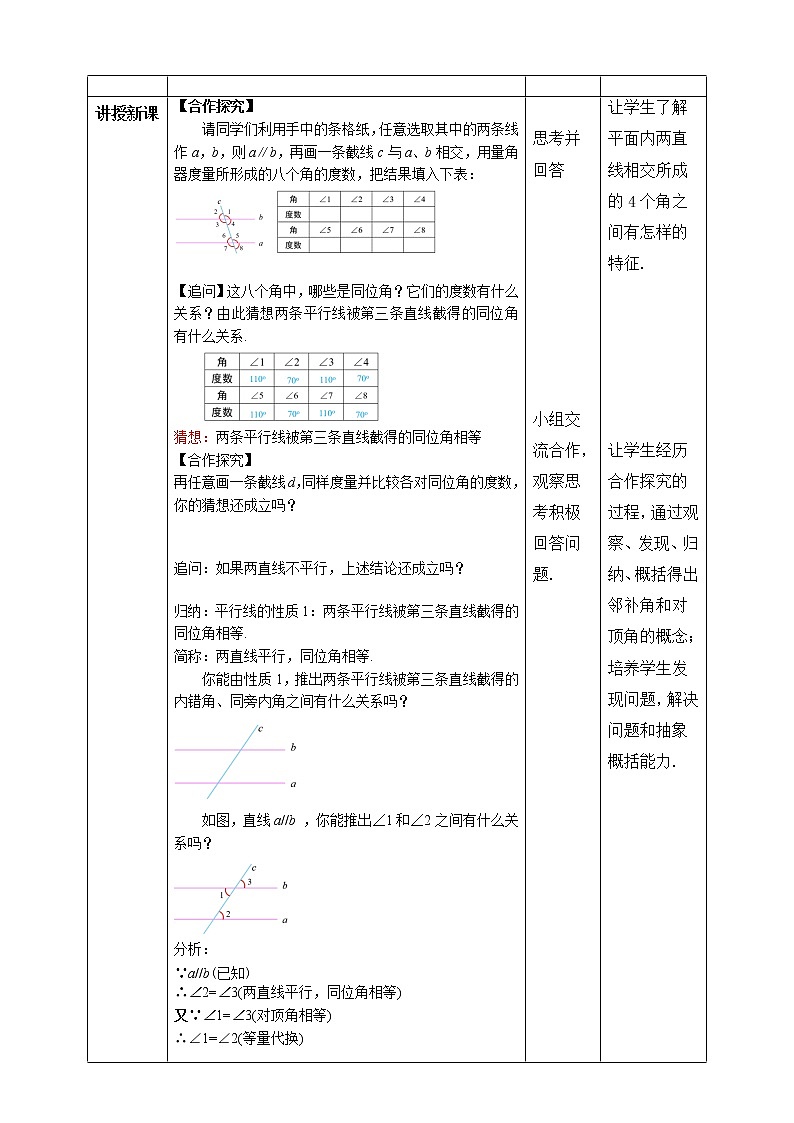
请同学们利用手中的条格纸，任意选取其中的两条线作a，b，则a∥b，再画一条截线c与a、b相交，用量角器度量所形成的八个角的度数，把结果填入下表
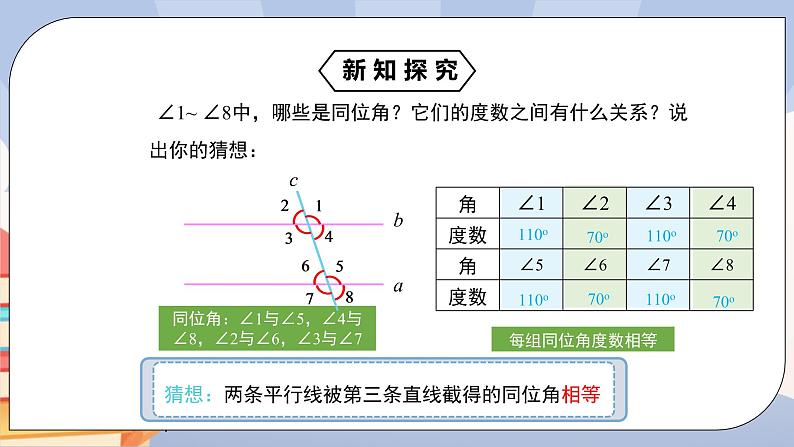
∠1~ ∠8中，哪些是同位角？它们的度数之间有什么关系？说出你的猜想：
同位角：∠1与∠5，∠4与∠8，∠2与∠6，∠3与∠7
猜想：两条平行线被第三条直线截得的同位角相等.
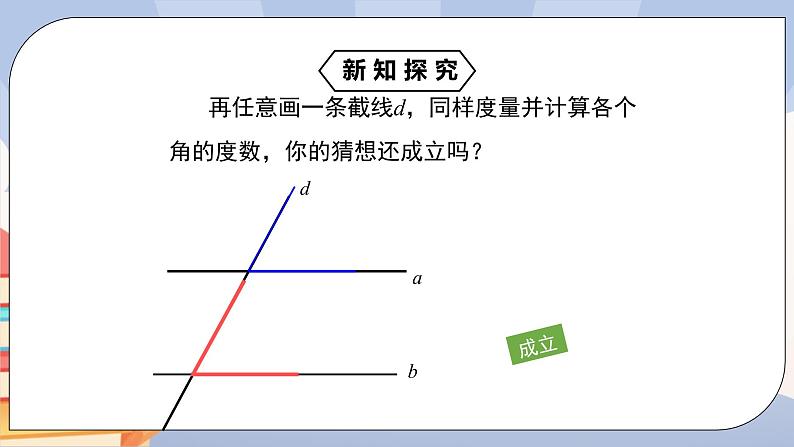
再任意画一条截线d，同样度量并计算各个角的度数，你的猜想还成立吗？
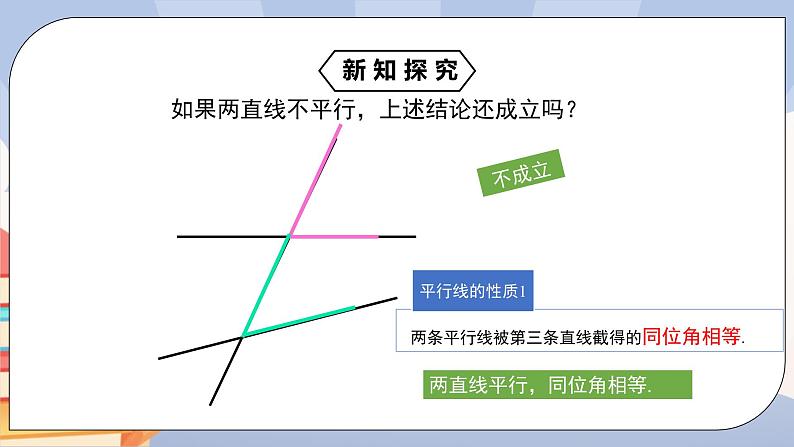
如果两直线不平行，上述结论还成立吗？
两直线平行，同位角相等.
类比判定1推出判定2，你能由性质1，推出两条平行线被第三条直线截得的内错角、同旁内角之间有什么关系吗？
如图，直线a//b ，你能推出∠1和∠2之间有什么关系吗？
(两直线平行，同位角相等)
两直线平行，内错角相等.
如图，直线a//b ，你能推出∠2和∠4之间有什么关系吗？
两直线平行，同旁内角互补.
性质3 两直线平行，同旁内角互补.
性质2 两直线平行，内错角相等.
性质1 两直线平行，同位角相等.
例：如图，是一块梯形铁片的残余部分，量得∠A100°，∠B 115°，梯形的另外两个角分别是多少度？
∴∠A+∠D180°
又∠A100°，∠B 115°
∴∠D80°∠C 65°
(两直线平行，同旁内角互补)
梯形的另外两个角分别是80°、65°.
1.如图，已知平行线AB、CD被直线AE所截 (1)从 ∠1=110可以知道∠2 是多少度,为什么？ (2)从∠1=110可以知道 ∠3是多少度,为什么？ (3)从 ∠1=110可以知道∠4 是多少度,为什么？
解：(1)∠2=110 ∵两直线行，内错角相等；
（2）∠3=110 ∵两直线平行, 同位角相等；
（3）∠4=70 ∵两直线平行,同旁内角互补.
2.如图，一条公路两次拐弯前后两条路互相平行.第一次拐的∠B是142，第二次拐的∠C是多少度？为什么？
解：∠C=142 ∵两直线平行,内错角相等.
3.如图，已知直线a，b被直线c所截，在括号内为下面各小题的推理填上适当的根据：
(1)∵ a//b，∴∠1∠3( )
(2) ∵∠1∠3，∴ a//b( )
(3)∵ a//b， ∴∠1∠2( )
(4) ∵ a//b， ∴∠1∠4180°( )
两直线平行，同位角相等
两直线平行，内错角相等
两直线平行，同旁内角互补
1、如图，将一块含有30°角的直角三角板的两个顶点分别放在直尺的两条平行对边上，若∠α＝135°，则∠β等于(　　)A．45° B．60° C．75° D．85°
2、如图，若∠1＝∠2，DE//BC，则①FG//DC；②∠AED＝∠ACB；③CD平分∠ACB；④∠1＋∠B＝90°；⑤∠BFG＝∠BDC，其中正确的结论是(　　)A．①②③　 B．①②⑤　C．①③④　 D．③④
3、如图，MN，EF 表示两面互相平行的镜面，光线 AB 照射到镜面 MN 上，反射光线为 BC，此时∠1=∠2；光线 BC 经过镜面 EF 反射后的光线为 CD，此时∠3=∠4.试判断 AB 与 CD 的位置关系，并说明理由.
解：AB//CD.理由如下：∵ MN//EF(已知)， ∴ ∠2=∠3(两直线平行，内错角相等).∵ ∠1=∠2，∠3=∠4(已知)，∴ ∠1=∠2=∠3=∠4， ∴∠1+∠2=∠3+∠4.∵ ∠ABC+∠1+∠2=180°， ∠BCD+∠3+∠4=180°(平角的性质)，∴ ∠ABC=∠BCD(等量代换).∴ AB//CD(内错角相等，两直线平行).