









人教版七年级下册5.3.1 平行线的性质精品教学ppt课件
展开1.理解平行线的性质及其与平行线的判定之间的关系.2.掌握平行线的三条性质,并能用它们进行简单的推理和计算.3.锻炼学生的动手操作能力,从中渗透数形结合、转化的数学思想和方法.
重点:探索和掌握平行线的性质并能进行简单的具体运用.难点:对平行线性质的探索和理解过程,平行线的判定和性质的区别.
平行线的判定方法是什么?
反过来,如果两条直线平行,同位角、内错角、同旁内角有什么关系呢?
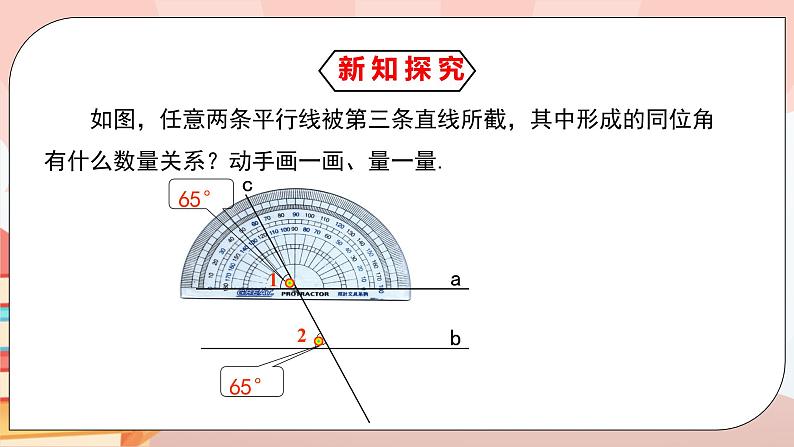
如图,任意两条平行线被第三条直线所截,其中形成的同位角有什么数量关系?动手画一画、量一量.
两条平行线被第三条直线所截,同位角相等.
简单说成:两直线平行,同位角相等.符号语言: ∵a∥b(已知) ∴∠1=∠2 (两直线平行,同位角相等)
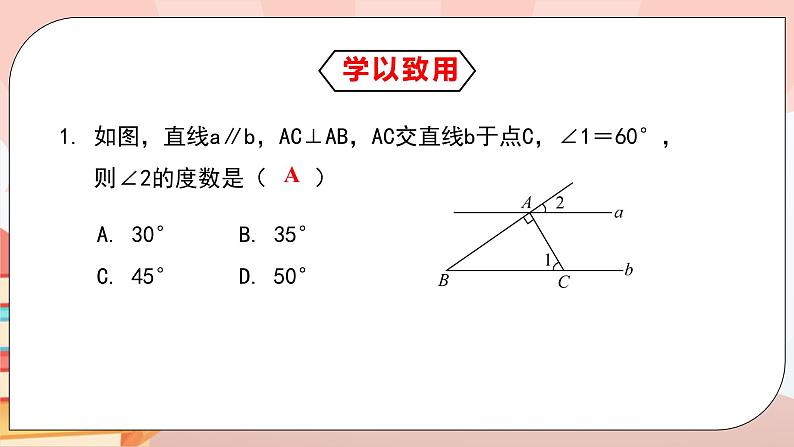
1. 如图,直线a∥b,AC⊥AB,AC交直线b于点C,∠1=60°, 则∠2的度数是( )
A. 30° B. 35° C. 45° D. 50°
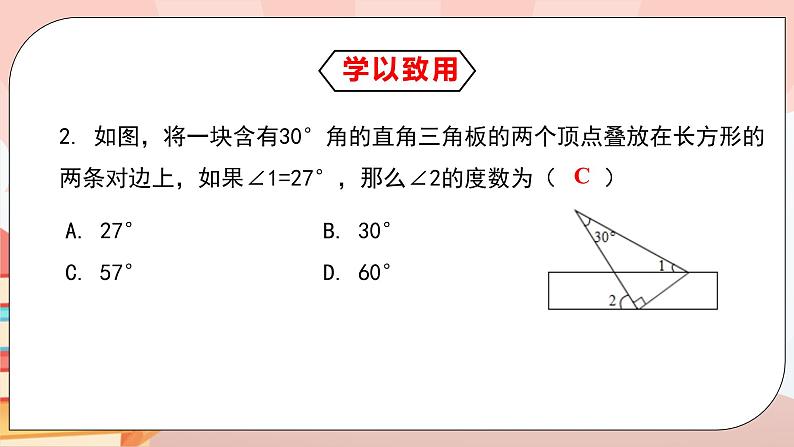
2. 如图,将一块含有30°角的直角三角板的两个顶点叠放在长方形的两条对边上,如果∠1=27°,那么∠2的度数为( )
A. 27° B. 30° C. 57° D. 60°
例题1. 如图,直线 a∥b,∠1 = 54°,∠2,∠3,∠4各是多少度?
解:∵a∥b,∠1=54° ∴∠4 =∠1 = 54°(两直线平行,同位角相等) ∠3 =180°-∠4 =180°- 54° =126° ∵∠2与∠1是对顶角 ∴∠2=∠1= 54°
1. 如图,已知a//b,那么2与3相等吗?为什么?
解:∵ a∥b ∴∠1=∠2(两直线平行,同位角相等) 又∵∠1=∠3(对顶角相等) ∴ ∠2=∠3(等量代换)
由此你有 什么发现?
2.由同样的方法,当a//b,时2与4有什么数量关系呢?
解:∠2+∠4=180°,理由如下: ∵ a∥b ∴∠1=∠2(两直线平行,同位角相等) 又∵∠1+∠4=180°(邻补角的性质) ∴∠2+∠4=180°
由此你又有 什么发现?
两条平行线被第三条直线所截,内错角相等.
简单说成:两直线平行,内错角相等.符号语言: ∵a∥b(已知) ∴∠2=∠3 (两直线平行,内错角相等)
两条平行线被第三条直线所截,同旁内角互补.
简单说成:两直线平行,同旁内角互补.符号语言: ∵a∥b(已知) ∴∠2+∠4=180° (两直线平行,同旁内角互补)
例2. 如图,是一块梯形铁片的残余部分,量得∠A = 100 °,∠B = 115 °,梯形的另外两个角分别是多少度?
解:∵梯形上、下底互相平行,DC//AB ∴∠A+∠D=180°,∠B+∠C=180° ∴∠D=180°-∠A=180°-100°=80° ∠C=180°-∠B=180°-115°=65° 即梯形的另外两个角分别是80°、65°.
例题3. A岛观察B岛,在北偏西35°方向,那么B岛观察A岛的方向是( ) A.南偏西55° B.南偏西35° C.南偏东35° D.南偏东55°
1. 如图,直线a、b被c所截,若a∥b,∠1=45°,∠2=65°,则∠3的度数为( )
A. 110° B. 115° C. 120° D. 130°
2. 如图,由AB∥CD可以得到( )A.∠1=∠2 B.∠2=∠3C.∠1=∠4 D.∠3=∠4
3. 如图,已知直线 a,b 被直线 c 所截,以下结论正确的有( ) ①∠1 =∠2; ②∠1 =∠3; ③∠2 =∠3; ④∠3+∠4 = 180°. A. 1个 B. 2个 C. 3个 D. 4个
4. 如图,要在公路的两侧铺设平行管道,如果公路一侧铺设的管道与纵向联通管道的角度为120°,那么,为了使管道对接,另一侧应以____角度铺设纵向联通管道,根据是__________________________.
两直线平行,同旁内角互补
问题:对比平行线的性质和判定方法,你能说出它们的区别吗?
例题4. 如图所示,AB∥CD,∠1=∠2. 试说明:BE∥PF .
解:∵ AB∥CD ∴ ∠ABP = ∠BPD ∵ ∠1 = ∠2 ∴ ∠ABP -∠1 = ∠BPD-∠2 即 ∠3 = ∠4 ∴ BE∥PF
1. 如图,如果 AB∥CD∥EF ,那么∠BAC + ∠ACE + ∠CEF =( )A.180° B.270°C.360° D.540°
2. 如图,推理填空: ∵1= 2(已知) ∴ AD//_____(________________________) ∴ BCD+_____=180(__________________________)
内错角相等,两直线平行
两直线平行,同旁内角互补
3. 如图,已知∠1=∠2,CE∥BF,试说明: AB∥CD.
解:AB//CD. 理由如下: ∵ CE∥BF ∴∠1=∠B ∵∠1=∠2 ∴∠2=∠B ∴ AB∥CD
思考:如图,若AB//CD,你能确定∠B、∠D与∠DEB的大小关系吗?说说你的看法.
解:过点E作EF//AB. ∴∠B=∠BEF. ∵AB//CD. ∴EF//CD. ∴∠D =∠DEF. ∴∠B+∠D=∠BEF+∠DEF=∠DEB. 即∠B+∠D=∠DEB.
两直线平行同旁内角互补
人教版七年级下册第五章 相交线与平行线5.3 平行线的性质5.3.1 平行线的性质完美版课件ppt: 这是一份人教版七年级下册第五章 相交线与平行线5.3 平行线的性质5.3.1 平行线的性质完美版课件ppt,文件包含531第1课时平行线的性质pptx、531第2课时平行线的性质与判定的综合应用pptx、RJ中学数学七年级下531平行线的性质第一课时教学详案docx等3份课件配套教学资源,其中PPT共32页, 欢迎下载使用。
初中数学人教版七年级下册5.3.1 平行线的性质教学课件ppt: 这是一份初中数学人教版七年级下册5.3.1 平行线的性质教学课件ppt,文件包含《531平行线的》精品课件pptx、《531平行线的性质》精品教学方案doc、《531平行线的性质》同步练习docx等3份课件配套教学资源,其中PPT共22页, 欢迎下载使用。
初中数学人教版七年级下册5.3.1 平行线的性质教学ppt课件: 这是一份初中数学人教版七年级下册5.3.1 平行线的性质教学ppt课件,共17页。PPT课件主要包含了复习引入,试试看,我知道啦,平行线的性质,可以简记为,知识拓展,请完成以下推理过程,例题选讲,大展身手,因为∠1=∠2等内容,欢迎下载使用。














