高中人教A版 (2019)5.3 导数在研究函数中的应用图文课件ppt

这是一份高中人教A版 (2019)5.3 导数在研究函数中的应用图文课件ppt，共35页。PPT课件主要包含了f′x0，极大值，极小值等内容，欢迎下载使用。

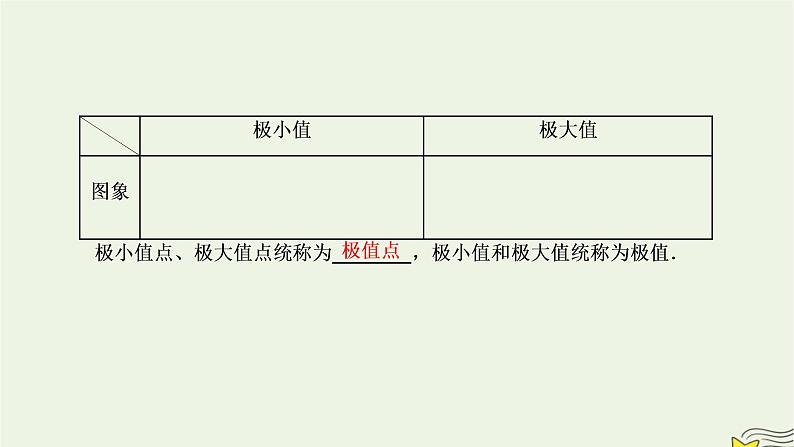
(一)教材梳理填空1．极小值、极大值的概念
[微提醒](1)极值是一个局部概念，极值只是某个点的函数值，与它附近点的函数值比较它是最大值或最小值，但并不意味着它在函数的整个定义域内是最大值或最小值．(2)一个函数在某区间上或定义域内的极大值或极小值可以不止一个．(3)函数的极大值与极小值之间无确定的大小关系．(4)函数的极值点一定出现在区间的内部，区间的端点不能成为极值点．(5)单调函数一定没有极值．
2．求函数y＝f(x)极值的方法一般地，求函数y＝f(x)的极值的方法是：解方程f′(x)＝0，当f′(x0)＝0时：(1)如果在x0附近的左侧f′(x)＞0，右侧f′(x)＜0，那么f(x0)是 ；(2)如果在x0附近的左侧f′(x)＜0，右侧f′(x)＞0，那么f(x0)是 ．
[微提醒]一般来说，“f′(x0)＝0”是“函数y＝f(x)在点x0处取得极值”的必要不充分条件．若可导函数y＝f(x)在点x0处可导，且在点x0处取得极值，那么f′(x0)＝0；反之，若f′(x0)＝0，则点x0不一定是函数y＝f(x)的极值点．
答案：(1)√　(2)√　(3)×
2．[多选]下列四个函数，在x＝0处取得极小值的是(　　)A．y＝x3 B．y＝x2＋1C．y＝|x| D．y＝2x答案：BC
题型一　极值的图象特征 [学透用活][典例1]　已知函数y＝f(x)，其导函数y＝f′(x)的图象如图所示，则y＝f(x)(　　)A．在(－∞，0)上为减函数B．在x＝0处取极小值C．在(4，＋∞)上为减函数D．在x＝2处取极大值
[解析]　由导函数的图象可知：x∈(－∞，0)∪(2,4)时，f′(x)>0；x∈(0,2)∪(4，＋∞)时，f′(x)<0，因此f(x)在(－∞，0)，(2,4)上为增函数，在(0,2)，(4，＋∞)上为减函数，所以函数f(x)在x＝0处取得极大值，x＝2处取得极小值，x＝4处取得极大值，因此选C.[答案]　C
解决函数极值与函数、导函数图象的关系问题时，应注意：(1)对于导函数的图象，重点考查导函数的值在哪个区间上为正，在哪个区间上为负，图象在哪个点处与x轴相交，在交点附近导函数的值是怎样变化的；(2)对于函数的图象，重点考查函数在哪个区间上单调递增，在哪个区间上单调递减，哪个点是极大值点，哪个点是极小值点．　　
解析：观察函数y＝xf′(x)的图象可以发现，当x∈(1，＋∞)时，xf′(x)>0，于是f′(x)>0，故函数f(x)在区间(1，＋∞)上是增函数，A正确；当x∈(－1,0)时，xf′(x)>0，于是f′(x)<0，当x∈(0,1)时，xf′(x)<0，于是f′(x)<0，故函数f(x)在区间(－1,1)上是减函数，B、C错误；由于f(x)在区间(0,1)上是减函数，在区间(1，＋∞)上是增函数，所以函数f(x)在x＝1处取得极小值，故D正确．答案：AD　
题型二　运用导数解决函数的极值问题 [学透用活][典例2]　(1)已知函数f(x)的导数f′(x)＝a(x＋1)(x－a)，若f(x)在x＝a处取到极大值，则a的取值范围是(　　)A．(－∞，－1)　　　　　B．(0，＋∞)C．(0,1) D．(－1,0)(2)求函数f(x)＝x2e－x的极值．
[解析]　(1)选D　f′(x)＝a(x＋1)(x－a)，若a<－1则，f(x)在(－∞，a)上单调递减，在(a，－1)上单调递增，∴f(x)在x＝a处取得极小值，与题意矛盾；若－10，则f(x)在(－1，a)上单调递减，在(a，＋∞)上单调递增，与题意矛盾，故选D.
(2)函数的定义域为R，f′(x)＝2xe－x＋x2·e－x·(－x)′＝2xe－x－x2·e－x＝x(2－x)e－x.令f′(x)＝0，得x(2－x)·e－x＝0，解得x＝0或x＝2.当x变化时，f′(x)，f(x)的变化情况如下表：
1．求函数极值的步骤(1)确定函数的定义域；(2)求导数f′(x)；(3)解方程f′(x)＝0得方程的根；(4)利用方程f′(x)＝0的根将定义域分成若干个小开区间，列表，判定导函数在各个小开区间的符号；(5)确定函数的极值，如果f′(x)的符号在x0处由正(负)变负(正)，则f(x)在x0处取得极大(小)值．
2．已知函数极值求参数时的注意点(1)根据极值点的导数为0和极值这两个条件列方程组，利用待定系数法求解．(2)因为导数值等于零不是此点为极值点的充要条件，所以利用待定系数法求解后必须验证充分性．　　
[对点练清]1．[已知极值求参数范围]若函数f(x)＝x3＋x2－ax－4在区间(－1,1)上恰有一个极值点，则实数a的取值范围为______．解析：由题意，f′(x)＝3x2＋2x－a，则f′(－1)f′(1)<0，即(1－a)(5－a)<0，解得12．[已知极值求参数]已知f(x)＝x3＋3ax2＋bx＋a2在x＝－1时有极值0，求常数a，b的值．
∴f(x)在R上为增函数，无极值，故舍去．当a＝2，b＝9时，f′(x)＝3x2＋12x＋9＝3(x＋1)(x＋3)．当x∈(－∞，－3)时，f(x)为增函数；当x∈(－3，－1)时，f(x)为减函数；当x∈(－1，＋∞)时，f(x)为增函数．∴f(x)在x＝－1时取得极小值，∴a＝2，b＝9.
3．[求极值]求函数f(x)＝3x3－3x＋1的极值．
题型三　函数极值的应用 [学透用活][典例3]　已知f(x)＝2ln(x＋a)－x2－x在x＝0处取得极值．(1)求实数a的值；(2)若关于x的方程f(x)＋b＝0的区间[－1,1]上恰有两个不同的实数根，求实数b的取值范围．
(1)研究方程根的问题可以转化为研究相应函数的图象问题，一般地，方程f(x)＝0的根就是函数f(x)的图象与x轴交点的横坐标，方程f(x)＝g(x)的根就是函数f(x)与g(x)的图象的交点的横坐标．(2)事实上利用导数可以判断函数的单调性，研究函数的极值情况，并能在此基础上画出函数的大致图象，从直观上判断函数图象与x轴的交点或两个函数图象的交点的个数，从而为研究方程根的个数问题提供了方便．　　
[对点练清]已知函数f(x)＝x3－3ax－1(a≠0)．若函数f(x)在x＝－1处取得极值，直线y＝m与y＝f(x)的图象有三个不同的交点，求m的取值范围．解：因为f(x)在x＝－1处取得极值且f′(x)＝3x2－3a，所以f′(－1)＝3×(－1)2－3a＝0，所以a＝1.所以f(x)＝x3－3x－1，f′(x)＝3x2－3，由f′(x)＝0，解得x＝－1或x＝1.当x<－1时，f′(x)>0；当－11时，f′(x)>0.所以由f(x)的单调性可知，
f(x)在x＝－1处取得极大值f(－1)＝1，在x＝1处取得极小值f(1)＝－3.作出f(x)的大致图象及直线y＝m如图所示：因为直线y＝m与函数y＝f(x)的图象有三个不同的交点，结合图象可知，m的取值范围是(－3,1)．
三、创新性——强调创新意识和创新思维　如何用二阶导数判断极值？能不能用一个简单的条件来判断导函数的图象是穿过x轴，还是碰一下就回头？如果碰一下就回头，那触碰点就成了导函数的极值点了，导函数的导函数在这一点就应当为0.反过来，如果导函数的导函数在此点处非零，此点就不是导函数的极值点，导函数的图象会在这里穿过x轴．上面的讨论说明：函数f(x)在驻点c处的导数f′(c)＝0而f″(c)≠0，则x＝c是f(x)的极值点．若f″(c)＞0，则f′(x)在x＝c附近递增到f′(c)＝0再递增，由负变正，所以f(x)由递减变为递增，在x＝c处取得极小值．