苏科版九年级上册2.4 圆周角课后作业题

九年级上册第二章 对称图形------圆

2.4.1圆周角（一）

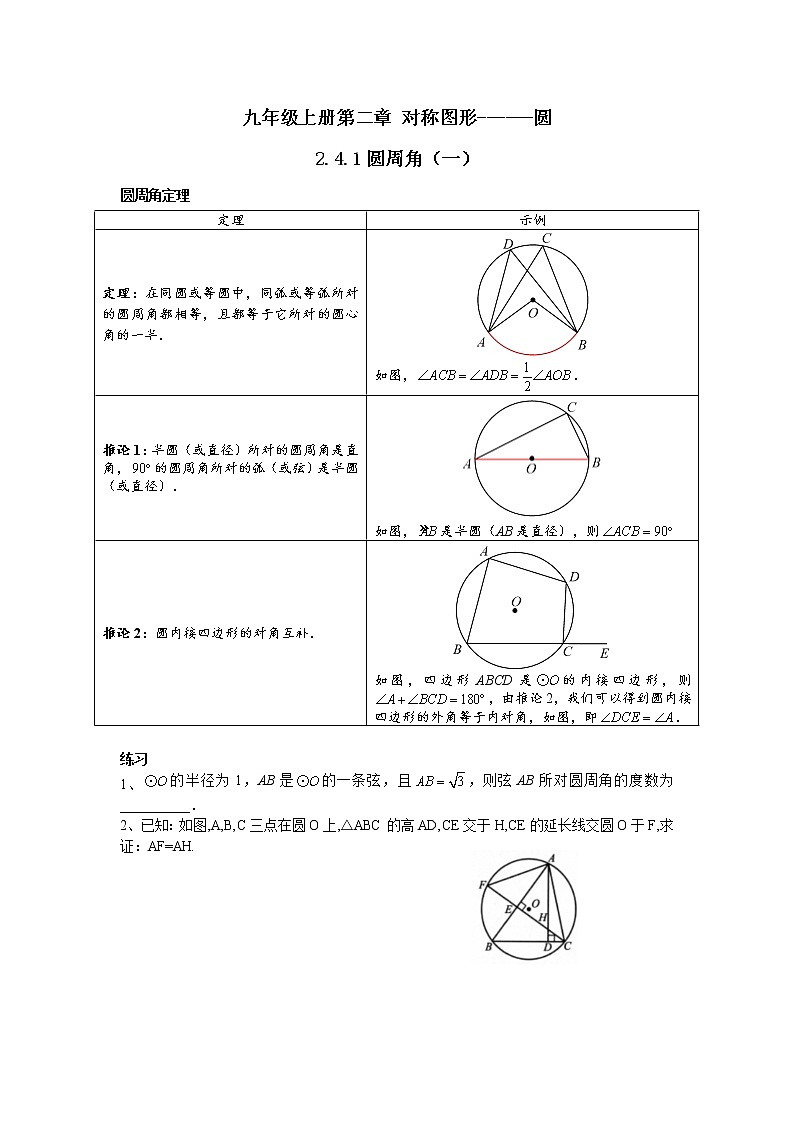
圆周角定理

练习

1、的半径为1，AB是的一条弦，且，则弦AB所对圆周角的度数为__________．

2、已知：如图,A,B,C三点在圆O上,△ABC的高AD,CE交于H,CE的延长线交圆O于F,求证：AF=AH.

3、如图，A，B，C，D为⊙O的四等分点，动点P从圆心O出发，沿O﹣C﹣D﹣O路线作匀速运动，设运动时间为t(秒)．∠APB=y(度)，则下列图象中表示y与t之间函数关系最恰当的是(    )

4、如图，△ABC内接于⊙O，且∠ABC=∠C，点D在弧BC上运动．过点D作DE∥BC，DE交AB的延长线于点E，连接BD．
（1）求证：∠ADB=∠E；
（2）求证：AD²=AC•AE．

5、如图，⊙O的半径为1cm，弦AB、CD的长度分别为cm，1cm，则弦AC、BD所夹的锐角α=_________．

6、如图,⊙O是△ABC的外接圆,D是弧ACB的中点,DE//BC交AC的延长线于点E,若AE=10,∠ACB=60°,求BC的长．

7、已知：如图所示,AB为O的直径,C是O外一点,BC交O于点E,AC交O于点D,∠D0E=60∘，求∠C的度数。

8、已知：在△ABC中，以AC边为直径的⊙O交BC于点D，在劣弧AD上取一点E使∠EBC=∠DEC，延长BE依次交AC于G，交⊙O于H。
（1）求证：AC⊥BH；
（2）若∠ABC=45°，⊙O的直径等于10，BD=8，求CE的长

9、如图，Rt△ABC中，AB⊥BC，AB=6，BC=4，P是△ABC内部的一个动点，且满足∠PAB=∠PBC，则线段CP长的最小值为________．

10、如图，已知AD是△ABC的外角∠EAC的平分线，交BC的延长线于点D，延长DA交△ABC的外接圆于点F，连接FB，FC．

（1）求证：FB=FC；
（2）若AB是△ABC外接圆的直径，∠EAC=120°，BC=6cm，求AD的长．

11、如下图，两圆相交于A，B两点，小圆经过大圆的圆心O，点C，D分别在两圆上，若，则的度数为_______．
 

12、如图，点A、B、C、D、E在⊙O上，且劣弧AE的度数为50°，则∠B+∠D的度数为______.

13、如图，⊙O的内接四边形ABCD两组对边的延长线分别交于点E、F．

（1）当∠E=∠F时，则∠ADC=_____°；

（2）当∠A=55°，∠E=30°时，求∠F的度数；

（3）若∠E=α，∠F=β，且α≠β．请你用含有α、β的代数式表示∠A的大小．

14、已知：如图，AB是⊙O的直径，CD为弦，且AB⊥CD于E，F为DC延长线上一点，连结AF交⊙O于M．
求证：∠AMD=∠FMC．

15、如图，圆内接四边形ABCD的两组对边延长线分别交于E、F，∠AEB、∠AFD的平分线交于P点．求证：PE⊥PF．
 

参考答案

1、60°或120°

2、证明：因为 ∠AFC=∠ABC
又易证∠AHE=∠ABC
那么∠AHE=∠AFC
又∠AEF=∠AEC(90°)
AE=AE
易证△AEF≌△AEH
∴AF=AH

3、C

4、（1）根据圆周角定理及平行线的性质不难求解；
（2）由（1）可得∠ADB=∠E，又∠A为公共角，且AB=AC，易得△ABD∽△ADE，利用相似三角形的性质即可得证．

5、75°

6、10

7、60°

8、连结AD

9、2

10、略

11、40°

12、155°

13、（1）90°；（2）∠F=40°；（3）∠A=

14、首先连接BM，由AB是⊙O的直径，根据直径所对的圆周角是直角，可得∠AMB=∠BMF=90°，又由AB⊥CD于E，可证得∠CMB=∠BMD，则可证得结论．

15、由圆内接四边形ABCD的两组对边延长线分别交于E、F，∠AEB、∠AFD的平分线交于P点，继而可得EM=EN，即可证得：PE⊥PF