人教B版 (2019)必修 第一册1.1.2 集合的基本关系说课ppt课件

这是一份人教B版 (2019)必修 第一册1.1.2 集合的基本关系说课ppt课件，文件包含112集合的基本关系pptx、112集合的基本关系doc等2份课件配套教学资源，其中PPT共44页， 欢迎下载使用。

理解集合之间包含与相等的含义，能识别给定集合的子集.
会用三种语言(自然语言、图形语言、符号语言)表示集合间的基本关系，并能进行转换，重点提升数学抽象和直观想象素养.
问题导学预习教材必备知识探究
互动合作研析题型关键能力提升
拓展延伸分层精练核心素养达成
WEN TI DAO XUE YU XI JIAO CAI BI BEI ZHI SHI TAN JIU
问题导学预习教材 必备知识探究
1.思考　你能发现下面两个集合之间的关系吗？(1)A＝{1，2}，B＝{1，2，3}；(2)A＝{x|1≤x≤2}，B＝{x|0≤x≤3}.
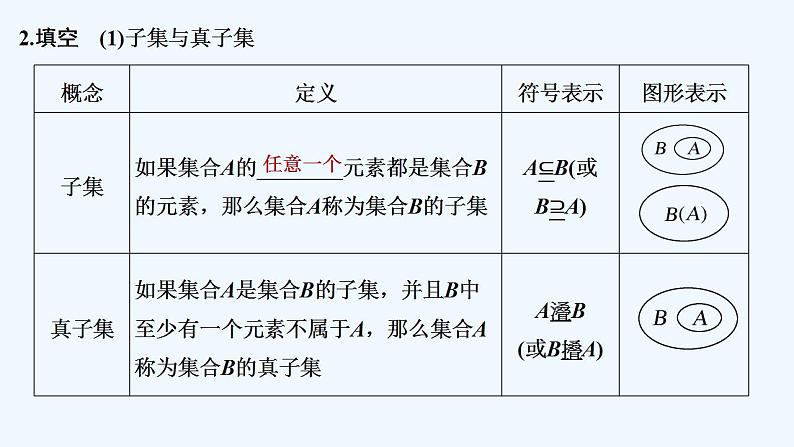
2.填空　(1)子集与真子集
(2)子集、真子集的性质①任意集合A都是它自身的______，即A⊆A.②空集是任意一个集合A的子集，即________.③对于集合A，B，C，如果A⊆B，B⊆C，那么________.④对于集合A，B，C，如果AB，BC，那么________.(3)一般地，如果集合A和集合B的元素__________，则称集合A与集合B相等，记作________，读作“A等于B”.
(4)由集合相等以及子集的定义可知：如果________且________，则A＝B；反之，如果A＝B，则________且________.
温馨提醒　(1){0}，∅，{∅}之间的区别与联系：{0}是含有一个元素0的集合，∅是不含任何元素的集合，因此∅⊆{0}，而{∅}是含有一个元素∅的集合，因此∅作为一个元素时，有∅∈{∅}，∅作为一个集合时，有∅⊆{∅}.(2)集合的子集、真子集个数的规律为：含n个元素的集合有2n个子集，有2n－1个真子集，有2n－2个非空真子集.写集合的子集时，空集和集合本身易漏掉.
3.做一做　(1)(多选)集合P＝{x|x2－1＝0}，T＝{－1，0，1}，则P与T的关系为(　　)
(2)下列图形中，表示M⊆N的是(　　)
HU DONG HE ZUO YAN XI TI XING GUAN JIAN MENG LI TI SHENG
互动合作研析题型 关键能力提升
例1 指出下列各对集合之间的关系： (1)A＝{－1，1}，B＝{(－1，－1)，(－1，1)，(1，－1)，(1，1)}；
题型一　集合间关系的判断
(2)A＝{x|x是等边三角形}，B＝{x|x是等腰三角形}；
解　(1)集合A的元素是数，集合B的元素是有序实数对，故A与B之间无包含关系.(2)等边三角形是三边都相等的三角形，等腰三角形是存在两边相等的三角形，故AB.
(3)A＝(－1，4)，B＝{x|x－5<0}；(4)M＝{x|x＝2n－1，n∈N*}，N＝{x|x＝2n＋1，n∈N*}.
解　(3)集合B＝{x|x<5}，用数轴表示集合A，B，如图所示，由图可知AB.
(4)由列举法知M＝{1，3，5，7，…}，N＝{3，5，7，9，…}，故NM.
1.判断集合关系的方法(1)观察法：一一列举观察.(2)元素特征法：首先确定集合的元素是什么，弄清集合元素的特征，再利用集合元素的特征判断关系.(3)数形结合法：利用数轴或维恩图.2.证明A＝B，只需证明A⊆B且B⊆A.3.证明集合间的包含关系，一般用定义.
(2)已知集合A＝{x|x<－2，或x>0}，B＝(0，1)，则(　　)A.A＝B B.ABC.BA D.A⊆B
解析　在数轴上分别表示出集合A，B，如图所示，由数轴知BA.
例2 (1)集合{a，b，c}的所有子集为______________________________________，__________________其中它的真子集有________个.
题型二　子集、真子集个数问题
∅，{a}，{b}，{c}，{a，b}，{a，c}，
{b，c}，{a，b，c}
解析　集合{a，b，c}的子集有：∅，{a}，{b}，{c}，{a，b}，{a，c}，{b，c}，{a，b，c}，其中除{a，b，c}外，都是{a，b，c}的真子集，共7个.
(2)写出满足{3，4}P⊆{0，1，2，3，4}的所有集合P.
解　由题意知，集合P中一定含有元素3，4，并且是至少含有三个元素的集合，因此所有满足题意的集合P为：{0，3，4}，{1，3，4}，{2，3，4}，{0，1，3，4}，{0，2，3，4}，{1，2，3，4}，{0，1，2，3，4}.
求给定集合的子集的两个注意点：(1)按子集中元素个数的多少，以一定的顺序来写；(2)在写子集时要注意不要忘记空集和集合本身.
训练2 已知集合A＝{(x，y)|x＋y＝2，x，y∈N}，试写出A的所有子集.
解　∵A＝{(x，y)|x＋y＝2，x，y∈N}，∴A＝{(0，2)，(1，1)，(2，0)}.∴A的子集有：∅，{(0，2)}，{(1，1)}，{(2，0)}，{(0，2)，(1，1)}，{(0，2)，(2，0)}，{(1，1)，(2，0)}，{(0，2)，(1，1)，(2，0)}.
题型三　利用集合关系求参数的值或取值范围
角度1　由集合相等求参数
例3 已知集合A＝{2，x，y}，B＝{2x，2，y2}，且A＝B，求x，y的值.
解　∵A＝B，所以集合A与集合B中的元素相同，
验证得，当x＝0，y＝0时，A＝{2，0，0}，这与集合元素的互异性相矛盾，舍去.
角度2　由集合间的包含关系求参数
例4 (1)已知集合A＝{x|－3≤x≤4}，B＝{x|2m－1解　∵B⊆A，①当B＝∅时，m＋1≤2m－1，解得m≥2.
解得－1≤m<2，综上得m的取值范围为[－1，＋∞).
(2)已知集合A＝{x|x2－4x＋3＝0}，B＝{x|mx－3＝0}，且B⊆A，求实数m的取值集合.
解　由x2－4x＋3＝0，得x＝1或x＝3.∴集合A＝{1，3}.①当B＝∅时，此时m＝0，满足B⊆A.
解之得m＝3或m＝1.综上可知，所求实数m的取值集合为{0，1，3}.
(1)若A⊆B，一定要分A＝∅和A≠∅两种情况讨论，不要忽视空集的情况.(2)对于用不等式给出的集合，已知集合的包含关系求相关参数的范围(值)时，常采用数形结合的思想，借助数轴解答，尤其要注意端点的取舍问题.
训练3 已知集合A＝{x|－2≤x≤5}，B＝{x|m＋1≤x≤2m－1}，若BA，求实 数m的取值范围.
解　(1)当B≠∅时，如图所示.
解这两个不等式组，得2≤m≤3.(2)当B＝∅时，由m＋1>2m－1，得m<2.综上可得，m的取值范围是{m|m≤3}.
对子集、真子集有关概念的理解(1)集合A中的任何一个元素都是集合B中的元素，即由x∈A，能推出x∈B，这是判断A⊆B的常用方法.(2)不能简单地把“A⊆B”理解成“A是B中部分元素组成的集合”，因为若A＝∅时，则A中不含任何元素；或者A＝B时，则A中含有B中的所有元素.(3)在真子集的定义中，A，B首先要满足A⊆B，其次至少有一个x∈B，但x∉A.
TUO ZHAN YAN SHEN FEN CENG JING LIAN HE XING SU YANG DA CHENG
拓展延伸分层精练 核心素养达成
1.已知集合A＝{x|x2－1＝0}，则有(　　)A.1∉A B.0AC.∅A D.{0}⊆A
解析　由已知得A＝{1，－1}，∴A，B，D都错误；∵∅是任何非空集合的真子集，∴C正确.
2.已知集合N＝{1，3，5}，则集合N的真子集个数为(　　)A.5 B.6 C.7 D.8
解析　集合N的真子集有：∅，{1}，{3}，{5}，{1，3}，{1，5}，{3，5}，共7个.
3.(多选)已知集合A＝{0，1，2}，B＝{1，m}，若B⊆A，则实数m的取值可以是(　　)A.0 B.2 C.1 D.3
解析　由A＝{0，1，2}，B＝{1，m}，B⊆A，得B＝{1，0}或B＝{1，2}.所以实数m的取值可以是0，2，故选AB.
4.下列正确表示集合M＝{－1，0，1}和N＝{x|x2＋x＝0}关系的维恩图是(　　)
解析　由N＝{x|x2＋x＝0}，得N＝{－1，0}.∵M＝{－1，0，1}，∴NM.
5.若集合A＝{x|x＝2k＋1，k∈Z}，B＝{x|x＝2k－1，k∈Z}，C＝{x|x＝4k－1，k∈Z}，则A，B，C的关系是(　　)A.CA＝B B.A⊆C⊆BC.A＝BC D.B⊆A⊆C
解析　∵A＝{x|x＝2(k＋1)－1，k∈Z}，B＝{x|x＝2k－1，k∈Z}，C＝{x|x＝2·2k－1，k∈Z}，∴CA＝B，故选A.
6.设A＝(2，4)，B＝{x|a－17.设集合A＝{x|x2＋x－6＝0}，B＝{x|mx＋1＝0}，则满足B⊆A的实数m的值所组成的集合为______________.
8.设集合A＝{－1，1}，集合B＝{x|x2－2ax＋1＝0}，若B≠∅，B⊆A，则a＝________.
解析　当B＝{－1}时，x2－2ax＋1＝0有两相等的实根－1，即a＝－1；当B＝{1}时，x2－2ax＋1＝0有两相等的实根1，即a＝1；当B＝{－1，1}时，不成立.故a＝±1.
9.判断下列集合间的关系：(1)A＝{x|x－3>2}，B＝{x|2x－5≥0}；(2)A＝{x∈Z|－1≤x<3}，B＝{x|x＝|y|，y∈A}.
(2)因为A＝{x∈Z|－1≤x<3}＝{－1，0，1，2}，B＝{x|x＝|y|，y∈A}，所以B＝{0，1，2}，所以BA.
10.已知集合A＝{x|x＜－1，或x＞4}，B＝{x|2a≤x≤a＋3}，若B⊆A，求实数a的取值范围.
解　当B＝∅时，只需2a＞a＋3, 即a＞3.
当B≠∅时，根据题意用数轴表示集合A，B如图所示，
解得a＜－4或2＜a≤3.综上，实数a的取值范围为{a|a＜－4，或a＞2}.
11.已知集合A＝{1，2}，B＝{(x，y)|x∈A，y∈A，(x－y)∈A}，则B的子集共有(　　)A.2个 B.4个 C.5个 D.8个
解析　B＝{(2，1)}，则其子集为∅，{(2，1)}，共2个，故选A.
12.(多选)若集合A＝{1，3，x}，B＝{x2，1}，且B⊆A，则满足条件的实数x可以是(　 　)
13.已知集合A＝{x|1≤x≤2}，集合B＝{x|1≤x≤a，a≥1}.
(1)若A＝B，求a的值；(2)若AB，求a的取值范围；
解　(1)若A＝B，则[1，2]＝[1，a]，∴a＝2.
(2)若AB，由图可知a的取值范围为(2，＋∞).
(3)若B⊆A，求a的取值范围.
解　若B⊆A，由图可知a的取值范围为[1，2].
14.已知集合A＝{x|x－a>0}，集合B＝{x|2－x<0}.若A⊆B，则实数a的取值范围为________.
解析　因为A＝{x|x>a}，B＝{x|x>2}，
A⊆B，所以A，B的关系如图所示.
由图可知a>2，当a＝2时，A＝{x|x>2}，此时A＝B，也满足A⊆B.所以实数a的取值范围为{a|a≥2}.